数据采集的原理及优化方法

将连续的模拟信号转换成计算机可接受的离散数字信号，需要两个环节：首先是采样，由连续模拟信号得到离散信号；然后再通过A/D转换，变为数字信号。

1.采样过程

采样过程如图4-21所示。采样开关周期性地闭合，闭合周期为T，闭合时间很短。采样开关的输入为连续函数f（t），输出函数f^∗（t）可认为是f（t）在开关闭合时的瞬时值，即脉冲序列f（T），f（2T）…f（nT）。

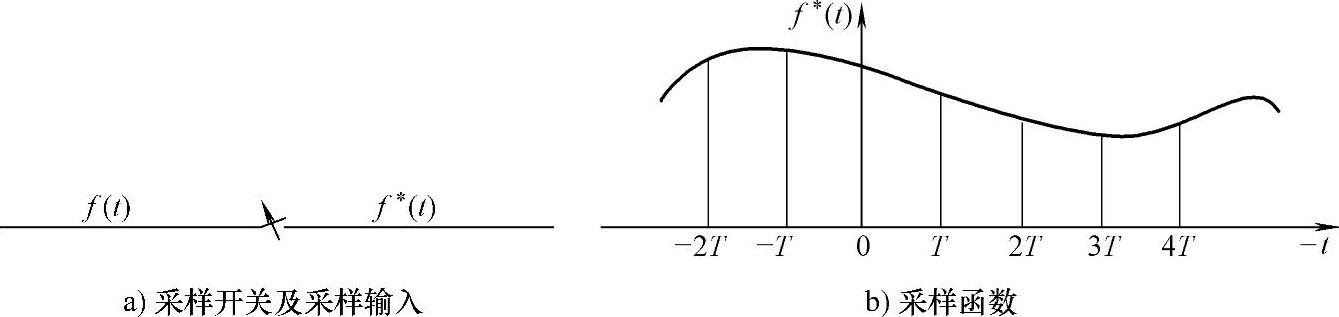
图4-21 采样过程示意图

设采样开关闭合时间为τ，则采样后得到的宽度为τ，幅值随f（t）变化的脉冲序列如图4-21a，采样信号f_s（t）可以看做是原信号f（t）与一个幅值为1的开关函数s（t）的乘积，即

s（t）是周期为T，脉冲宽度为τ，幅值为1的脉冲序列，如图4-22b所示。因此，采样过程实质上是一种调制过程，可以用一乘法器来模拟，如图4-22c所示。

由于脉冲宽度τ远小于采样周期T。因此可近似认为τ趋近于零，用单位脉冲函数δ（t）来描述，单位脉冲函数定义为

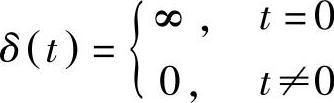
图4-22 采样过程原理图

且

即其宽度为零，面积为1。(www.xing528.com)

单位脉冲序列δ_T（t）可表示为

式（4-31）中δ（t-nT）为t-nT=0时，即t=nT处的单位脉冲，如图4-23所示。

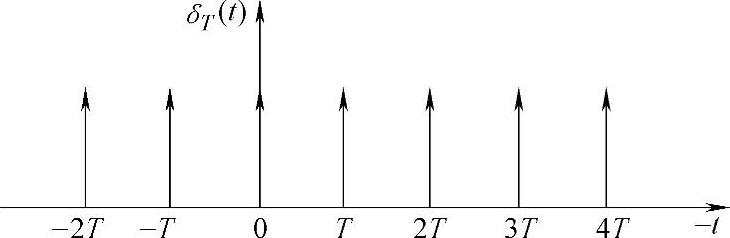
图4-23 单位脉冲序列

因此，采样信号为

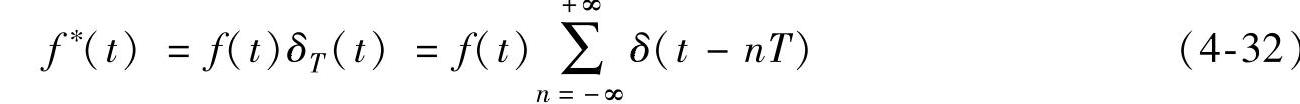
2.采样定理

香农采样定理：对一个有限频谱（-ω_max＜ω＜ω_max）的连续信号，当采样频率ω_s≥2ω_max时，采样函数才能不失真地恢复到原来的连续信号。

采样定理为数据采集系统确定采样频率奠定了理论基础，采样定理所规定的最低的采样频率，是数据采集系统必须遵守的规则。在实际使用时，由于：

1）信号f（t）的最高频率难以确定，特别是当f（t）中有噪声时，则更为困难。

2）采样理论要求在取得全部采样值后才能求得被采样函数，而实际上在某一采样时刻，计算机只取得本次采样值和以前各次采样值，而必须在以后的采样值尚未取得的情况下进行计算分析。因此，实际的采样频率取值高于理论值，一般为信号最高频率的5～10倍。