实际滤波器的幅频特性及截止频率原理

1.理想滤波器

（1）理想低通滤波器模型 理想滤波器是一个理想化的模型，是根据滤波网络的某些特性理想化而定义的，是一种物理不可实现的系统。但对它的研究，有助于理解滤波器的传输特性，并且由此导出的一些结论，可作为实际滤波器传输特性分析的基础。

理想滤波器具有矩形幅值特性和线性相移特性，理想低通滤波器的幅频和相频特性如图4-7所示。其频率响应函数、幅频特性、相频特性分别为

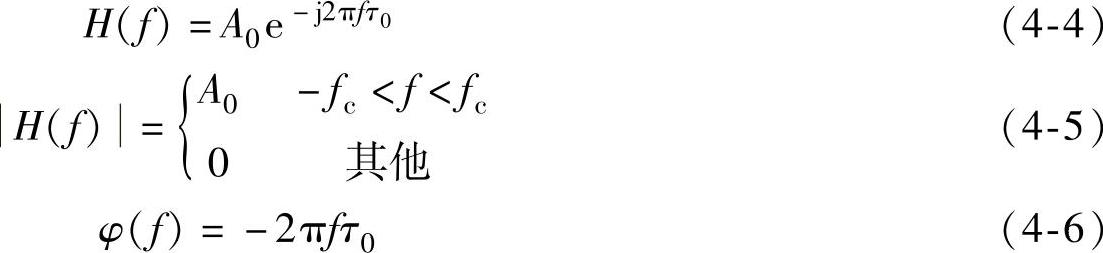
图4-7 理想低通滤波器的幅频和相频特性

这种理想低通滤波器，将信号中低于截止频率f_c的频率成分予以传输，而无任何失真；将高于f_c的频率成分则完全衰减掉。

（2）理想低通滤波器的脉冲响应 根据线性系统的传输特性，当δ函数通过理想滤波器时，其脉冲响应函数h（t）应是频率响应函数H（f）的逆傅里叶变换，由此有

理想滤波器的脉冲响应函数h（t）的波形如图4-8所示，这是一个峰值位于τ₀时刻的sinc（t）型函数。

理想滤波器是一种物理概念，实际上理想滤波器是不可能实现的，因为h（t）的波形表明，在输入δ（t）到来之前，滤波器就应该早有与该输入相对应的输出，显然，任何滤波器都不可能有这种“先知”，所以，理想滤波器是不可能存在的。可以推论，理想的高通、带通、带阻滤波器都是不存在的。实际滤波器的频域图形不可能出现直角锐变，也不会在有限频率上完全截止。实际滤波器的频域图形将延伸到∣f∣→∞，所以一个滤波器对信号中通带以外的频率成分只能极大地衰减，却不能完全阻止。

图4-8 理想滤波器的脉冲响应函数h（t）

2.实际滤波器

（1）实际滤波器的基本参数 对于理想滤波器，只需规定截止频率就可以说明它的性能，因为在截止频率f_c1、f_c2之间的幅频特性为常数A₀。截止频率以外则为零，如图4-9所示。而对于实际滤波器，由于它的特性曲线没有明显的转折点，通频带中幅频特性也并非常数，因此需要用更多的参数来描述实际滤波器的性能，主要参数有纹波幅度、截止频率、带宽、品质因数、倍频程选择性等。

1）纹波幅度d。在一定频率范围内，实际滤波器的幅频特性可能呈波纹变化。其波动幅度d与幅频特性的平均值A₀相比，越小越好，一般应远小于-3dB，即。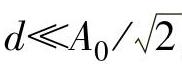

图4-9 理想带通与实际带通滤波器的幅频特性

2）截止频率f_c。幅频特性值等于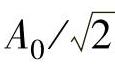所对应的频率称为滤波器的截止频率。以A₀为参考值，对应于-3dB点，即相对于A₀衰减3dB。若以信号的幅值平方表示信号功率，则所对应的点正好是半功率点。

3）带宽B和品质因数Q值 上下两截止频率之间的频率范围称为滤波器带宽，或-3dB带宽，单位为Hz。带宽决定着滤波器分离信号中相邻频率成分的能力——频率分辨力。

在电工中，通常用Q代表谐振回路的品质因数。在二阶振荡环节中，Q值相当于谐振点的幅值增益系数，Q=1/2ξ（ξ为阻尼率）。对于带通滤波器，通常把中心频率f₀和带宽B之比称为滤波器的品质因数Q。例如一个中心频率为500Hz的滤波器，若其中-3dB带宽为10Hz，则称其Q值为50。Q值越大，表明滤波器分辨力越高。

4）倍频程选择性W。在两截止频率外侧，实际滤波器有一个过渡带，这个过渡带的幅频曲线倾斜程度表明了幅频特性衰减的快慢，它决定着滤波器对带宽外频率成分衰阻的能力。通常用倍频程选择性来表征。所谓倍频程选择性，是指在上截止频率f_c2与2f_c2之间，或者在下截止频率f_c1与f_c1/2之间幅频特性的衰减值，即频率变化一个倍频程时的衰减量

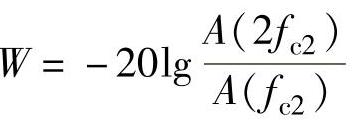
或

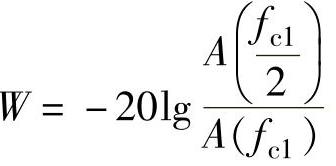
倍频程衰减量以dB/oct表示（oct为倍频程）。显然，衰减越快（即W值越大），滤波器选择性越好。

对于远离截止频率的衰减率也可用10倍频程衰减数表示，即dB/10oct。

5）滤波器因数（或矩形系数）λ。滤波器选择性的另一种表示方法，是用滤波器幅频特性的-60dB带宽与-3dB带宽的比值

来表示。理想滤波器λ=1，通常使用的滤波器λ=1～5。有些滤波器因器件影响（例如电容漏阻等），阻带衰减倍数达不到-60dB，则以标明的衰减倍数（如-40dB或-30dB）带宽与-3dB带宽之比来表示其选择性。

（2）RC调谐式滤波器的基本特性 在测试系统中，常用RC滤波器，因为在这一领域中，信号频率相对讲是不高的，而RC滤波电路简单，抗干扰性强，有较好的低频性能，并且选用标准阻容元件也容易实现。

1）一阶RC低通滤波器。一阶RC低通滤波器的典型电路及其幅频、相频特性如图4-10所示。(www.xing528.com)

图4-10 一阶RC低通滤波器的典型电路及其幅频、相频特性

设滤波器的输入电压信号为x（t）输出为y（t），电路的微分方程式为

令τ=RC，称时间常数。对上式取拉普拉斯变换，可得传递函数、频率响应函数、幅频特性及相频特性如下：

或

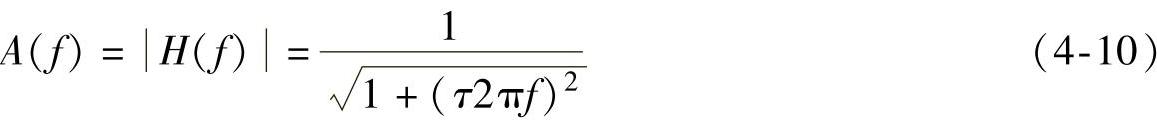
φ（f）=-arctan2πfτ （4-11）

分析可知，当f≪1/2πτ，A（f）=1，此时信号几乎不受衰减地通过，并且φ（f）-f也近似于线性关系。因此，可认为在此情况下，RC低通滤波器近似为一个不失真传输系统。

当f=1/2πτ时，A（f）=1/2，此即滤波器的-3dB点，此时对应的频率即为上截止频率，可知，RC值决定着上截止频率，因此，适当改变RC参数时，就可以改变滤波器截止频率。

当f1/2πτ时，输出y（t）与输入x（t）的积分成正比，即

此时RC滤波器起着积分器的作用，对高频成分的衰减为-20dB/（10oct）（或-6dB/oct）。如要加大衰减率，应提高低通滤波器的阶数，可以将几个一阶低通滤波器串联使用。

2）RC高通滤波器 图4-11所示为RC高通滤波器的典型电路及其幅频、相频特性。

设输入信号电压为x（t），输出为y（t），则微分方程式为

图4-11 RC高通滤波器的典型电路及其幅频、相频特性

同理，令RC=τ，则RC高通滤波器的传递函数、频率响应函数、幅频特性、相频特性如下：

或

f=1/2πτ时，A（f）=1/2，滤波器的-3dB截止频率为f=1/2πτ；当f1/2πτ时，A（f）≈1，φ（f）≈0，即当f相当大时，幅频特性接近于1，相移趋于零，此时RC高通滤波器可视为不失真传输系统；当f≪1/2πτ时，RC高通滤波器的输出与输入的微分成正比，起着微分器的作用，即

3）RC带通滤波器。带通滤波器可以看成是低通滤波器和高通滤波的串联组合，RC带通滤波器典型电路及其幅频相频特性如图4-12所示。

串联后的传递函数、频率响应函数、幅频特性、相频特性如下：

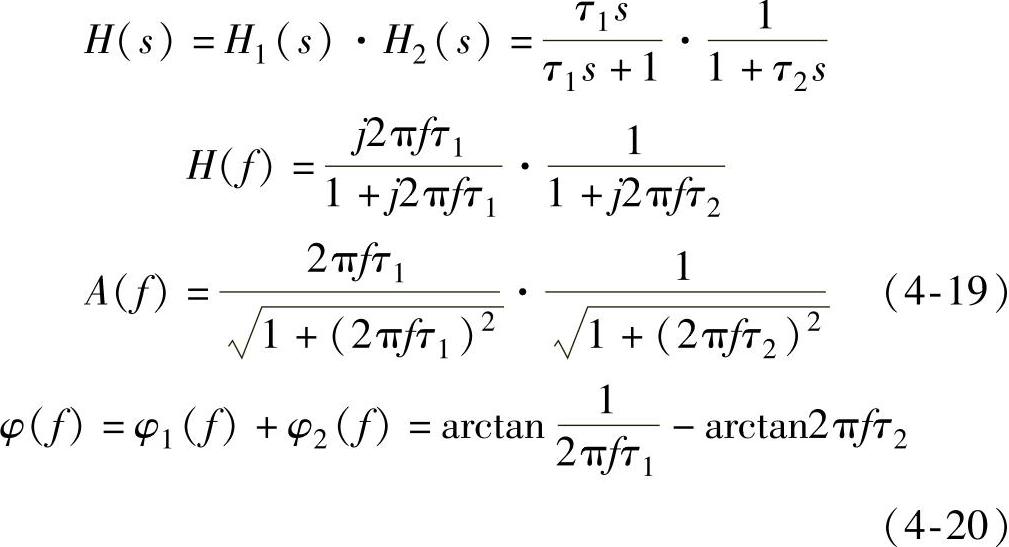
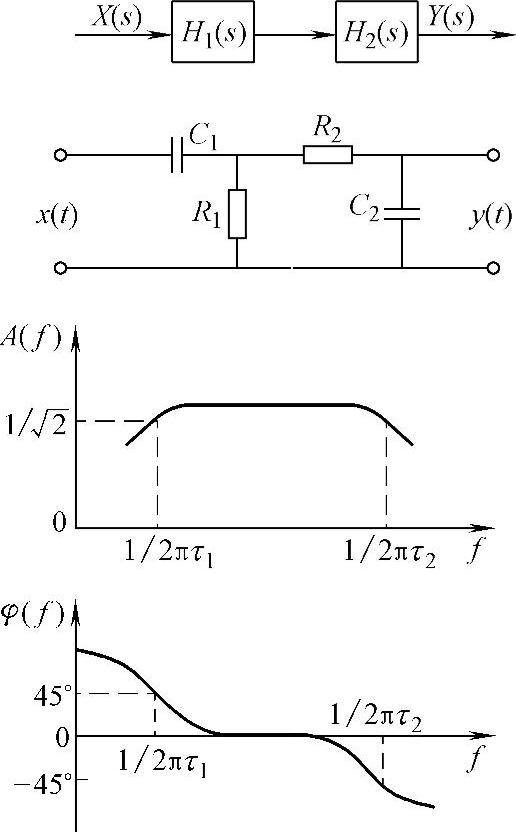
图4-12 RC带通滤波器典型电路及其幅频、相频特性

分析可知，当f=1/2πτ₁时，A（f）=1/2，此时对应的频率f_c1=1/2πτ₁，即原高通滤波器的截止频率，此时为带通滤波器的下截止频率；当f=1/2πτ₂时，A（f）=1/2，可认为是f1/2πτ₁，对应于原低通滤波器的截止频率，此时为带通滤波器的上截止频率。分别调节高、低通滤波器的时间常数τ₁、τ₂，就可以得到不同的上、下截止频率和带宽的带通滤波器。但是应注意，当高、低通两级串联时，应消除两级耦合时的相互影响，因为后一级成为前一级的“负载”，而前一级又是后一级的信号源内阻。实际上两级间常用射极输出器或者用运算放大器进行隔离。所以实际的带通滤波器常常是有源的。有源滤波器由RC调谐网络和运算放大器组成。运算放大器既可作为级间隔离作用，又可起信号幅值的放大作用。