滤波是消除噪声的一种有效方法,平滑本质上是一种数字滤波技术。滤波器在配置上一般应靠近A/D转换器;平滑在非实时应用情况下,一般用软件方法实现。对稳态信号可采用动态平滑(dynamical averaging)技术,以便在消除噪声的前提下得到相对平稳的读数。对动态信号可采用模拟滤波器,既滤除噪声,又可实现抗混叠滤波。模拟滤波器的截止频率设计在数据采集器的最高采样率的1/2处,从而保证了抗混叠滤波作用的实现。
滤波器作为一种选频电路,它可以使信号中的某些频率成分以固定的增益通过,而在这些频率以外的成分被极大地衰减,所以说滤波器是实现信号和干扰、噪声分离的关键器件,也是最常用的信号调理电路之一。
对于一个滤波器,能通过它的频率范围称为该滤波器为频率通带,被它抑制或极大地衰减的频率范围称为频率阻带,通带与阻带的交界点称为截止频率。
滤波器可以用不同的方法进行分类。如按通带和阻带的分布不同划分,滤波器可分为低通、高通、带通和带阻滤波器,如图4-6所示。按信号处理的性质划分可分为模拟滤波器和数字滤波器两大类;按滤波器电路中是否含有有源器件,滤波器可分为有源滤波器和无源滤波器;若按滤波器传递特性划分,则可分为巴特沃斯滤波器、切比雪夫滤波器、线性相位滤波器和贝赛尔滤波器等。
图4-6所示为这四种滤波器的幅频特性,图4-6a是低通滤波器,从0~f2频率之间,幅频特性平直,它可以使信号中低于f2的频率成分几乎不受衰减地通过,而高于f2的频率成分受到极大地衰减;图4-6b表示高通滤波器,与低通滤波器相反,从频率f1~∞,其幅频特性平直。它使信号中高于f1的频率成分几乎不受衰减地通过,而低于f1的频率成分将受到极大地衰减;图4-6c表示带通滤波器,它的通频带在f1~f2之间,它使信号中高于f1和低于f2的频率成分可以不受衰减地通过,而其他成分受到衰减;图4-6d表示带阻滤波器,与带通滤波器相反,阻带在频率f1~f2之间,它使信号中高于f1和低于f2的频率成分受到衰减,其余频率成分几乎不受衰减地通过。(https://www.xing528.com)
上述四种滤波器中,在通带与阻带之间存在一个过渡带。在过渡带内,信号受到不同程度的衰减。这个过渡带是滤波器所不希望的,但也是不可避免的。
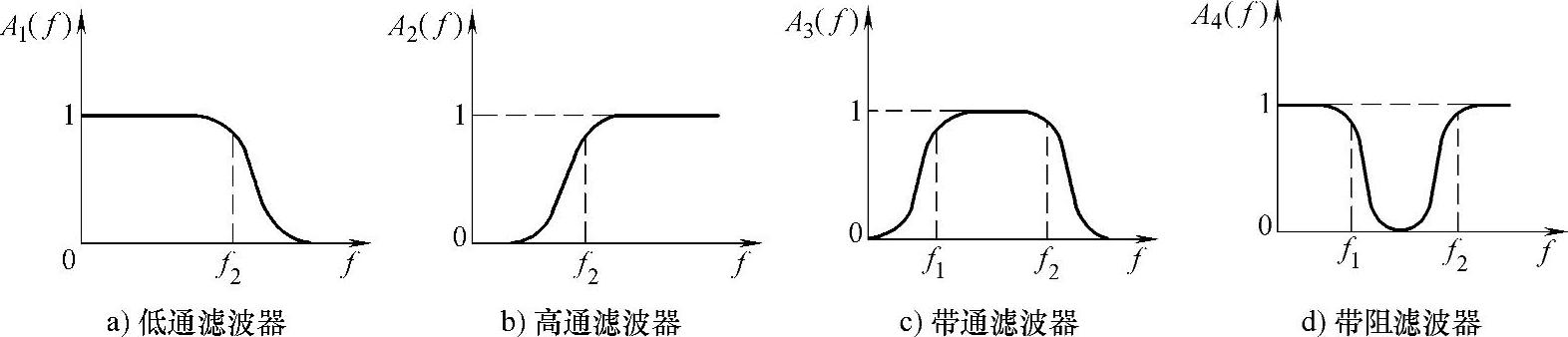
图4-6 滤波器的幅频特性
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




