帕累托优化：Z、M、P与效率的曲线分析及示例解析

假设相关系数的数值（从统计角度关于消耗，成本和特定污染排放）是c＝1.5，m＝3，p＝5。据式（9-91），对于任意有效的c，我们可以计算出单个个体的最优值（不是帕累托）和最小值。

表9-5 选定相关参数下的最优值

注：源自于Yantovsky，EandZack，Y.，2000。

关于Z、M、P与效率的曲线如图9-16所示。当效率接近某一个值时，它们随着最小值增长反映出投资的增加量。显示了所有这三个最佳值η和三个极小值的关系。箭头显示了效率增加的方向。如果我们考虑换热器，优化参数可以是在管壁中的温降。在该情况下，箭头方向相反。

表9-6 帕累托优化结果示例

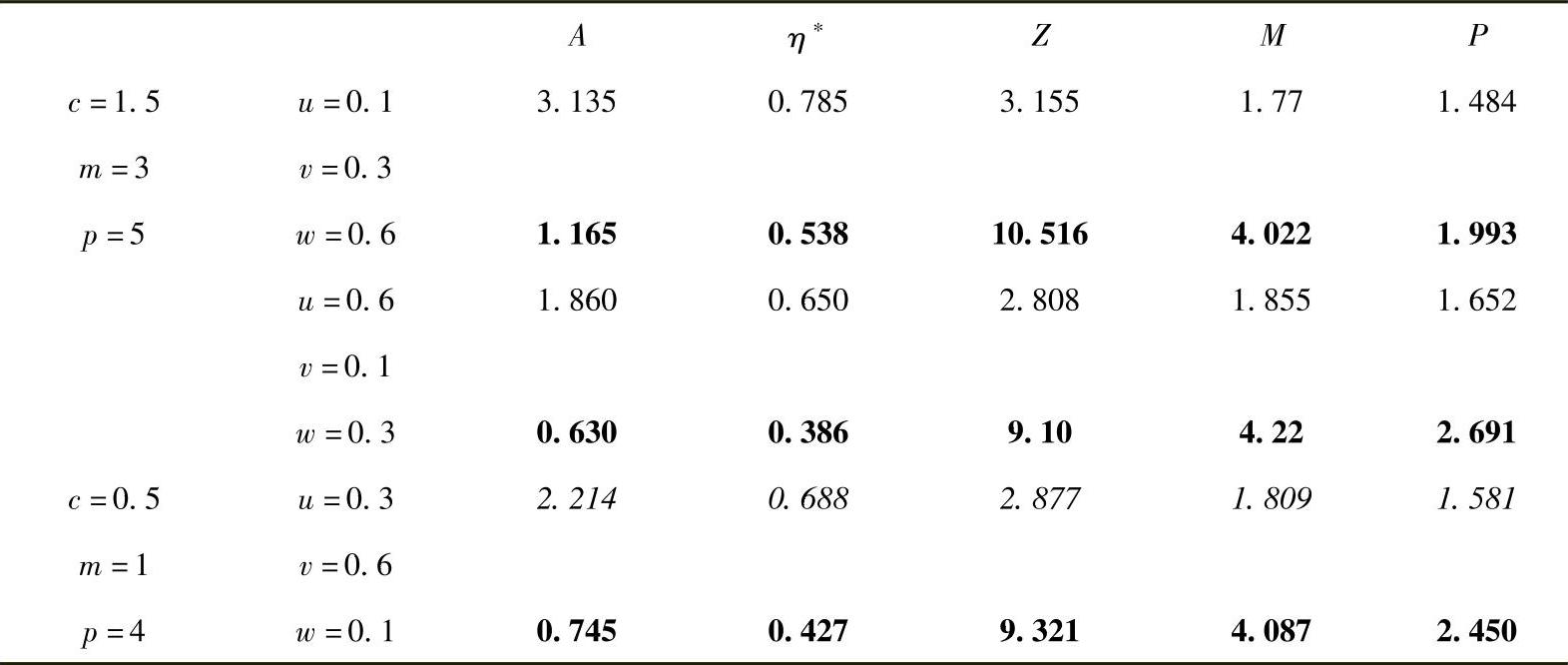
注：源自于Yantovsky，E.，2000。(www.xing528.com)

表9-11 显示了以矩形方框表示社会期望的特性曲线及其预测。其中显示了三个独立的最优解。

表9-6 给出了在给定两组相关系数c、m和p，以及三个权重系数情况下帕累托优化的数值解。当的权重系数从0.1增加到0.6时，的消耗指标Z由3.155下降到2.808或从10.516下降到9.10。第二组c、m、p和相关数字如上表斜体部分。

该表格显示了帕累托最优化效率随权重系数u、v、w值变化的敏感性，这足够做出有依据的优化决策。在一篇有趣的关于换热器设计的论文中，D.Sama（1993）感到遗憾因为已经告诉了他的学生。

……他们肯定只按照精确的经济性优化参数进行设计。采取其他措施都会被认为是异类的，因此，我让他们去研究圣杯之类的，称为“全局最优值”……全局最优值只是存在于理想状况中，寻找他们是徒劳的。

只有在设计师不理解其真正需要的东西时，我们才同意这种说法。如果他选择的不只是一个参数，而是选择任意几个目标函数和特定的权重系数，他有可能得到全局最优值。这就是帕累托最优值。

为了建立联系投资和传递的简单模型，让我们在三维坐标系中（-成本-污染），找到一个能量转换对象的帕累托优化的解析解。三个相关参数应该借助于统计数据获取。这种方法值得引起能源工程设计者和政策制定者的关注。