实际气体条件下的压缩机与透平效率优化

在压比较高的情况下，实际气体对压缩和膨胀过程的影响极为重要。在分析超临界布雷顿和朗肯循环时，这是个典型的极限条件。当实际的超临界CO₂气体经过压缩和膨胀并流经一系列高压透平和压缩机时，大多数热力学书籍中的等熵公式已不再适用。

因此，为了获得有价值的结果，必须制定更普遍的计算程序和公式来计算在致密气体区压缩机和透平的效率。

作这个分析的目的是基于实际气体模型和常用的热力学状态方程，推导压缩机和透平的等熵、多变效率。

Kouremenos、Kakatsios（1985）和Wiederuch（1988）对实际气体的压缩和膨胀过程作了分析，并已作为标准VDI2045-2：1993被应用。

基于任意形式的热力学状态方程和在上一章节中描述的VCD，Gorski（1997）提出一个较完整的方法解决此类问题。

在压缩和膨胀过程分析中，常用的术语是多变效率。它指的是在等熵、多变以及相应的焓增过程中参数的变化，如图3-1所示。

压缩和膨胀的多变效率_ηpc、η_pe分别为

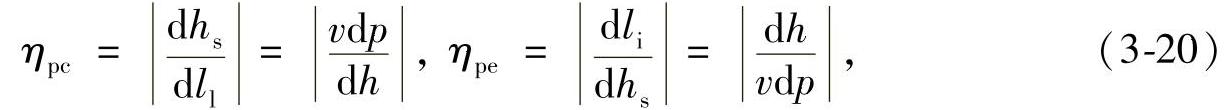
式中，dh_s＝-vdp是等熵绝热过程中的焓变，比技术功变化dl_t是指在实际过程中的焓升dh。

焓变随初压和体积的变化而变化：

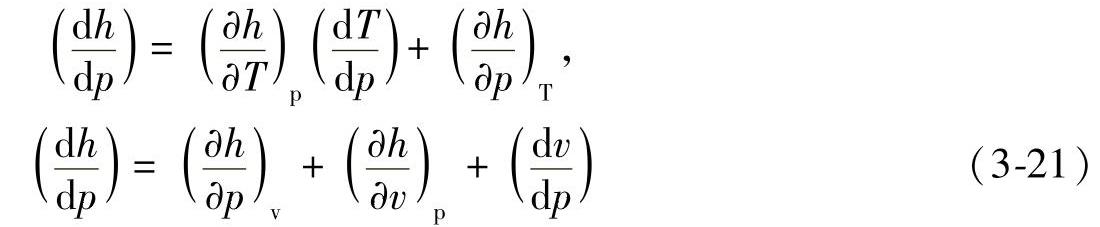
通过热力学第一定律和麦克斯韦关系及VCD，式（3-6）和式（3-7）定义的数学推导给出了绝热膨胀过程中温度和压力的直接变化关系（Gorski，1997）：

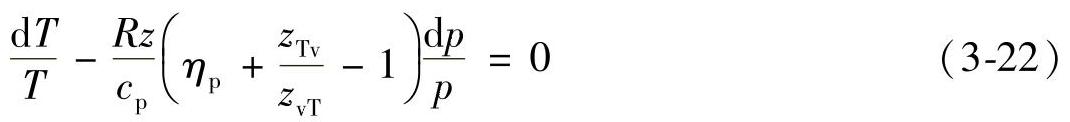
压力和比容增大的相似关系式为

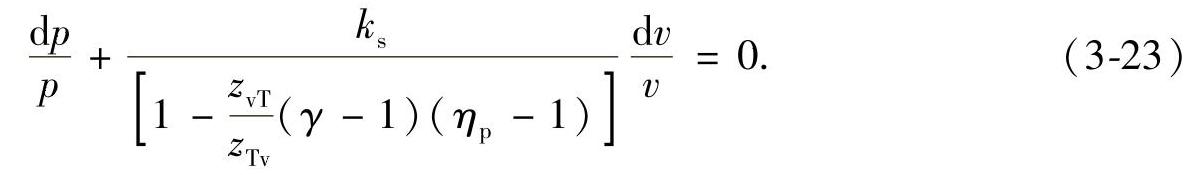(www.xing528.com)

式中，η_p≡η_pc；Κ_s为等熵指数；γ是比热容比

需要指出的是，若是压缩过程，式（3-22）和式（3-23）的多变效率应改为它的倒数，即η_p≡1/η_pc。

式（3-22）和式（3-23）中的参数不是常数，而是通过迭代，得到初态1和终态2间的均值，表示为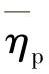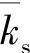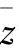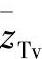，，，，…，从而关系式可以合并表示为类似于理想气体模型形式。

对式（3-23）和式（3-24）取无穷小和积分，对应结果分别为

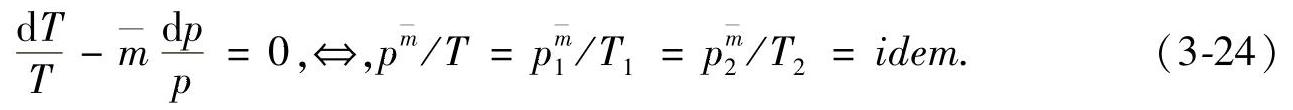
和

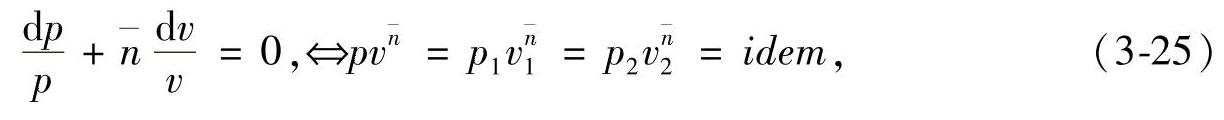
实际气体的平均压缩指数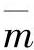、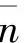分别为（Gorski，1997）：

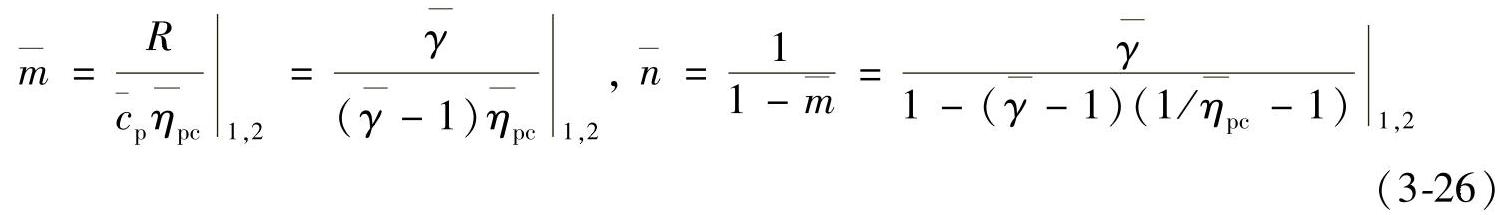
在致密气体区，所有的热力学基本过程更加完整的描述和符号表示见表3-2。

表3-2 实际致密气体典型过程的广义指数

注：源自于Gorski，J.andChemielniak，T.1993。

显然，在理想气体的情况下，根据式（3-13）和其他著名的热力学原理，以上介绍的公式中所有的系数都是常数，可以直接引入到式（3-24）和式（3-25）的积分形式中。