气体混合物的状态方程及热力学描述方法优化

在文献中，有大量有用的液体混合模型（Bejan，2006；OrbeyandSandler，1998；Span，2000）。这些模型在结构和准确性上有所不同。一组模型通过应用附加属性参数描述混合物行为。例如，Span（2000）列出的许多模型发展了附加吉布斯自由焓G^ex（T，p，）和附加亥姆霍兹自由能A^ex（T，ρ，）。

要使用这些模型，纯组分和混合物在给定的温度和压力下必须有相同的状态（Orbey and Sandler，1998）。这个前提下，考虑到所涉及的组分和覆盖的流体区域时，这些模型并不适用于大多数工程问题。这时状态方程可以很便捷地计算混合物的热力学性质。这些方程大多是压力显式方程，正如已经建立的三次方状态方程。由于其简单的数学结构，三次方状态方程在许多技术应用中仍广泛使用（Bejan，2006；OrbeyandSandler，1998）。然而，对于精度要求较高的技术应用，利用三次方状态方程计算混合物性能时存在较大的缺陷，主要表现在液相热特性和热量属性的描述上。

诸如Bender方程（1973）的经验状态方程，进一步描述了混合物的性质，特别是在同性区域。这些模型也是压力显式形式。Bender用混合规则描述与系数和温度相关的复合状态方程。Starling（1973）将混合原理用于状态方程中的每个系数（Ma¨der，1991）。

其他工作为广义对应态模型在混合物中的应用奠定了基础（Span，2000）。在此工作基础上，Sun和Ely（2005）提出了确切的形状因子概念。最近，Trusler等（Span，2000），发表了关于天然气和类似混合物的两个独立的广义对应态模型。一个是应用到较宽区域的方程，另一个仅限于密闭输送区。

这个较宽区域模型结果的平均准确性，接近或甚至比其他常用的天然气方程略好。上述混合物模型、天然气新模型和其他气体混合物模型，由混合物独立变量密度ρ、温度T和摩尔组分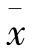三个参数的亥姆霍兹自由能的基本方程确定。类似于纯物质的基本方程，函数A（ρ，T，x）可以分为两部分：一为A⁰，表示在给定密度ρ、温度T和成分时的理想气体混合物属性；二为A^r，考虑到残余混合物属性（SpanandWagner，1996）。

利用亥姆霍兹自由能的无量纲形式ϕ＝A/（RT），式（3-14）化为

式中，δ是混合物的折合密度；τ是混合物折合温度的倒数。它们是由

δ＝ρ/ρ_ref，τ＝T_ref/T，（3-16）及该混合物的密度ρ_ref和温度T_ref确定的比函数

N种给定组分的理想气体混合物的无量纲形式亥姆霍兹自由能（Orbey和San-dler，1998）为

在流体混合物中，ϕ⁰_0i是组分i在理想气体状态下亥姆霍兹自由能的无量纲形式；x_i是组分的摩尔分数。在x_i中术语x_i解释混合过程的熵增。

在多种流体的近似计算中，残余混合物对比态亥姆霍兹自由能ϕ^r为(www.xing528.com)

式中，ϕ⁰_0i是第i种组分对比态亥姆霍兹自由能；Δϕ^r为偏离函数。每个组分的对比态亥姆霍兹自由能取决于混合物对比态参数δ和τ；偏离函数取决于混合物的组分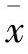。作为解释，这个表达式的结构分别对应Tillner-Roth（1993）、Lemmon（1996）、Lemmon和Jacobsen（1999）的模型。同样的，Span（2000）试图通过基于近似的多流体模型，实现准确描述非理想混合物体系的热力学性质。

由式（3-19）可知，混合物对比态亥姆霍兹自由能ϕ^r是由两个不同的部分组成（Span，2000）：

1）考虑了所有混合组分线性组合的残余部分；

2）偏离函数。

一般来说，偏离函数的作用，在残余混合物的对比态亥姆霍兹自由能方程中不如纯组分方程的作用大。

总之，基于近似多流态的气体混合物基本状态方程包括：

●考虑混合物所有成分的纯物质方程；●用于混合物密度ρ和温度T依赖于混合物组分的对比态函数，Tr＝T_r（x）；

●取决于对比态混合密度、对比态混合物的温度倒数和混合物成分的偏离函数Δϕ^r。

在工程实践中，为许多液态物质包括纯净物和混合物制定标准时，这些模型发挥着主要作用（Span，2000；Wagner and Kretzschmar，2008）。部分计算机应用程序允许引进这些模型，以模拟许多先进的化学和能量转换过程。Wagner和Overhoff（2006）在软件包“ThermoFluids”及IAPWS标准（Wagner andKretzschmar，2008），还有其他商业软件（Ruhr Universitat，2007）开发了一些最流行的软件程序。由于采用了一些非常方便的在线计算功能，NIST Chemistry WebBook（2007）和两个软件套件：ASPEN和Chemical Logic等发挥着主导的作用。