CO2热力学特性及混合物特性解析

几十年来，从工程的角度出发，CO₂在许多工业过程和应用中极为重要。它作为溶剂主要在化学工业用于超临界流体提取以及提高原油回采率。目前的一些研究进展表明它也适合于新的跨临界循环以及有利于生态安全的空调热泵系统。自上个世纪末，G.Lorenzen开展开创性工作以来，CO₂作为制冷剂（R-744），在汽车空调系统中的应用已不断增长。

作为煤或烃类等燃料燃烧排气的主要成分，CO₂是造成大气污染排放和温室效应的主要原因。CO₂的捕获和利用，在未来能源的转换系统中起着主要的作用。发电系统中捕捉CO₂的另一种方法是通过半封闭O₂/CO₂燃气轮机循环，即燃烧氧_-化石燃料的混合物并利用再循环的CO₂作为稀释气体。

在许多公开文献中，CO₂的热力学状态和流体输运特性得到广泛认同，（ht-tp：//airliquide，2008；www.chemicalogic，2008；SpanandWagner，1996；Vesovicetal.，1990）。热力学手册（Gorski，1997）给出CO₂的几个重要参数：这些参数说明了CO₂的材料匹配性能、主要危害以及安全的数据表。

大多数热力学性质（Span and Wagner，1996），例如CO₂在水溶液中的溶解度（Kerrick and Jacobs，1981；Ma¨der，1991），可以用适当的PVT关系或状态方程（EOS）来描述（Span，2000）。相关系（Phase Relations）可以从H₂O和CO₂的相图得出，同样也可以得到CO₂-H₂O系统相图，如图3-1所示。

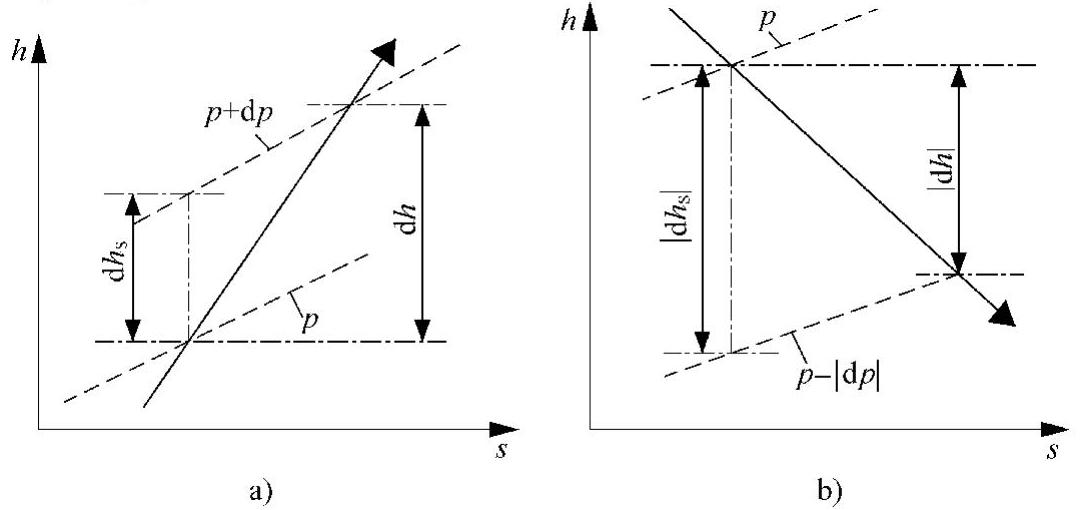
图3-1 基本的多变压缩（a）和膨胀（b）过程（Gorski，1997，获许发表）

现有广泛使用的关于CO₂热力学性质的数据发表在著名的《二氧化碳标准》中（Span and Wagner，1996）。Span和Wagner（1996）推导的状态方程涵盖从流体三相点温度到高达826.85℃，压力可达8000bar。Span和Wagner（1996）推出一个具有代表性的CO₂热力学性质的新方程，这是一个在亥姆霍兹自由能A确定并得到证实的基本经验方程。这个基本状态方程由两个独立的变量表述：无量纲形式的密度ρ和温度T。根据目前的热力学方法，无量纲亥姆霍兹自由能ϕ＝A/RT通常分为理想气体的部分ϕ^o和剩余的实际气体部分ϕ^r：

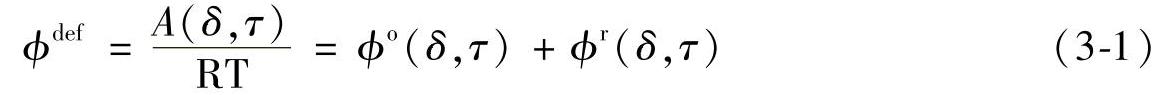
式中，δ＝ρ/ρ_c为对比密度，即实际密度ρ与临界密度ρ_c之比；τ＝Τ_c/Τ为对比温度的倒数，温度Τ与临界温度Τ_c之比的倒数（下标c表示流体密度和温度的临界值）。

此处，流体中一个组分的亥姆霍兹自由能描述为密度和温度的函数。然而，这只是基本方程的一个形式，事实上，所有的纯CO₂热力学性质，均可以由这个方程的合并、变形进行计算（见文献Span and Wagner，1996中的表3和本章中的表3-1）。

采用基于维里压缩性推导式（VCD）计算（Gorski，1997）流体性质的方法更为简单。

表3-1 按照对比态亥姆霍兹函数和维里压缩方程表示的热力学函数

（续）

对选定的热力学参数进行计算时，表3-1给出VCD方程和经典的表示法（Span and Wagner，1996）的主要关系比较。VCD符号体系的使用简化了所有重要热力参数的数学计算表达式。例如：

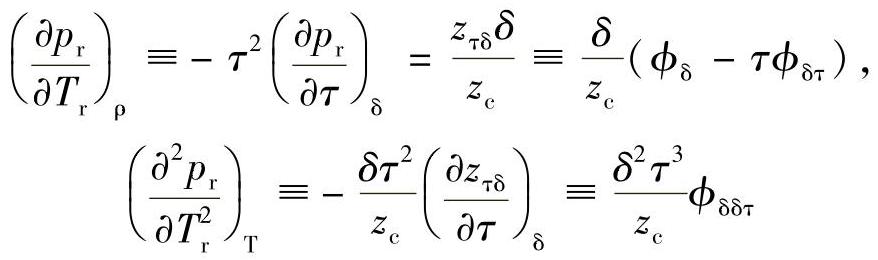
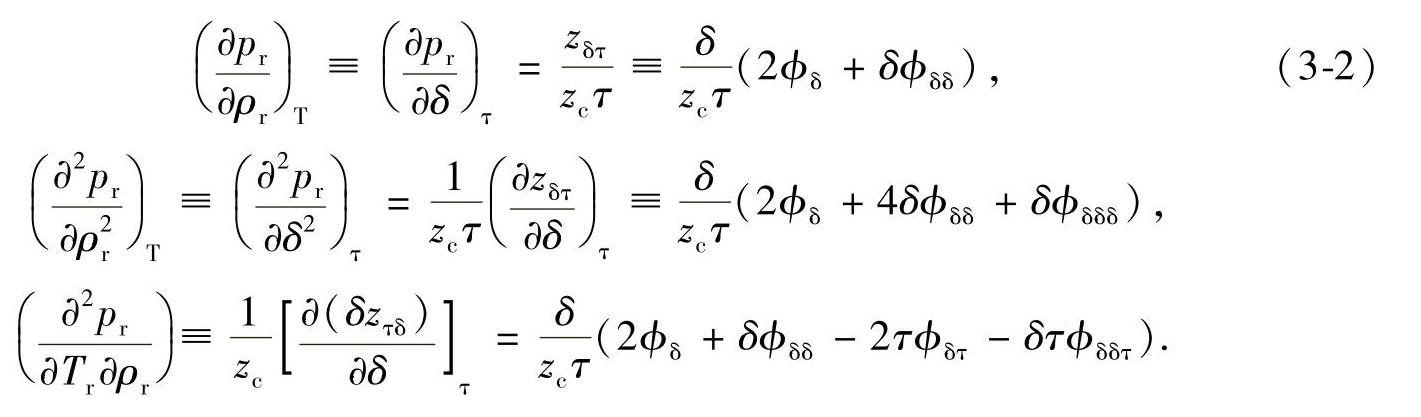
式中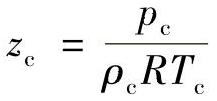，为热力学临界点处压缩因子和

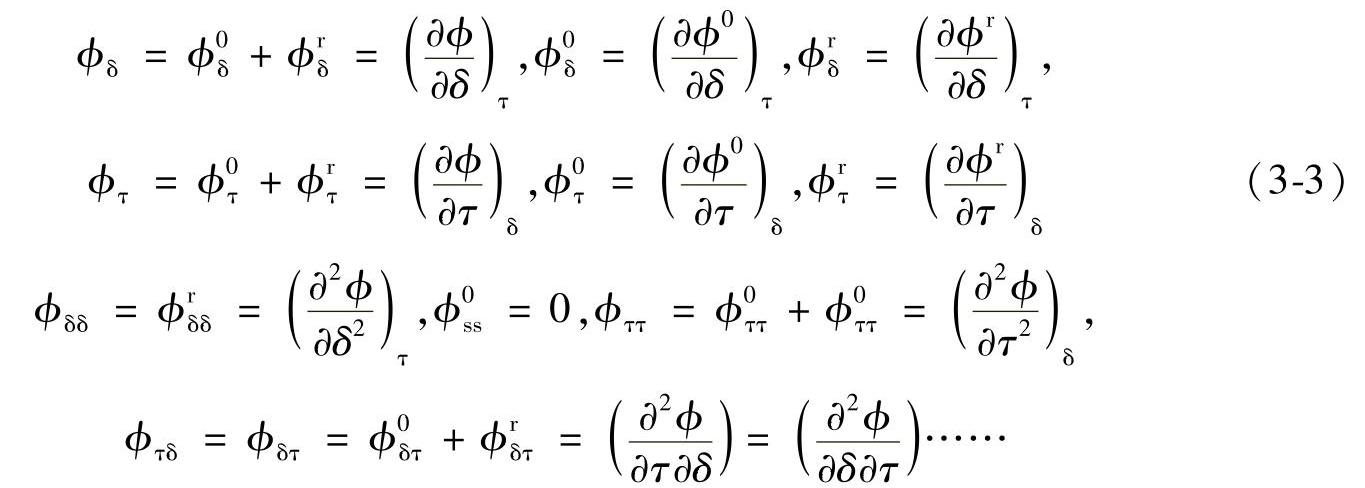
这些量可以直接从式（3-1）的显式形式获得并由VCD简单定义（Gorski，1997；Gors-kiandChmielniak，1993）：

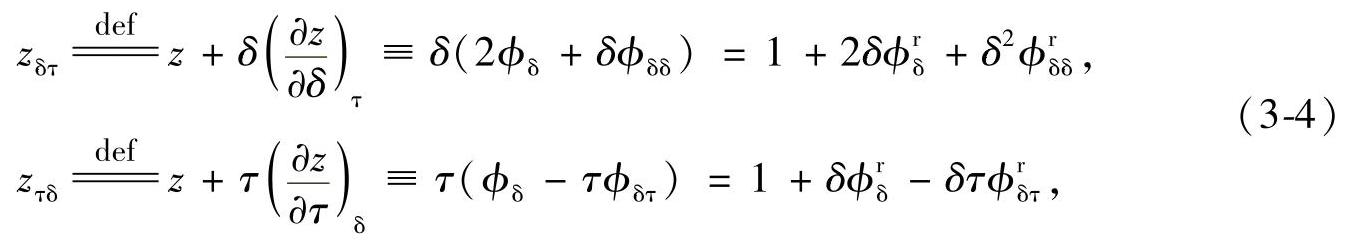
这些无量纲参数（与热力学临界点参数的比值）在工程实践中非常有用，它们体现了实际的可压缩流体和理想可压缩流体之间的差异。

表示它们物理意义的附属关系式与非常有名的可压缩流体的体积膨胀系数β、等温压缩系数κ、热膨胀系数ε直接相关。(www.xing528.com)

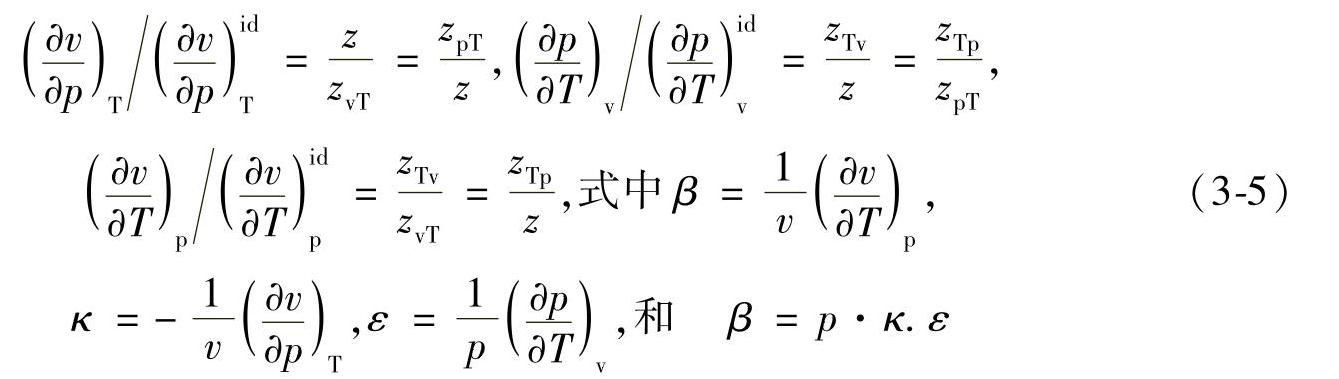
式（3-2）～式（3-4）和式（3-6）中的VCD参数只随状态变量的绝对值和对比参数值的变化而变化。假定对比态密度为δ＝ρ/ρ_c，对比态温度的倒数为τ＝Τ_c/Τ时，则（Gorski，1997；GorskiandChmielniak，1993）：

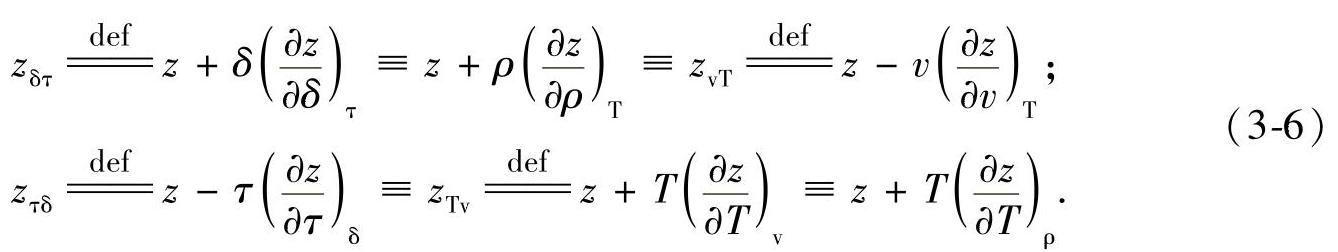
这些附属关系式可以由任何相联或传统变换形式的状态方程（EOS）和两个选定的独立变量推导出。在一个显式的状态方程（EOS）中，就压力P（压比π＝p_r＝p/p_c）和温度T（和τ＝Τ_c/Τ）而言，正确的VCD参数定义如下：

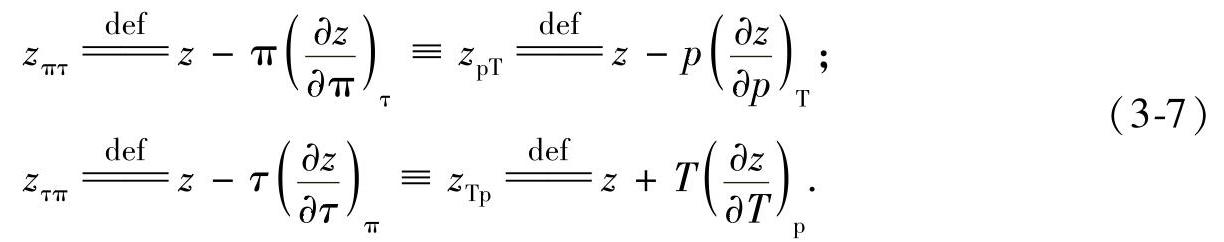
通过消去式（3-6）第二个下标，有时可以使用VCD的简式，但这些函数不是独立的（尤其是当z_Tp≠z_Tv，zΤδ≠zτπ时）：

Ψ（T，p，ρ）＝0↔p＝p（T，ρ），（3-8）和

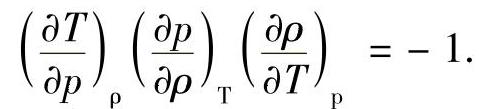
从式（3-5）和式（3-8），我们会发现

z_Tv＞z＞z_vT，z_Tp＞z_pT＞z，和

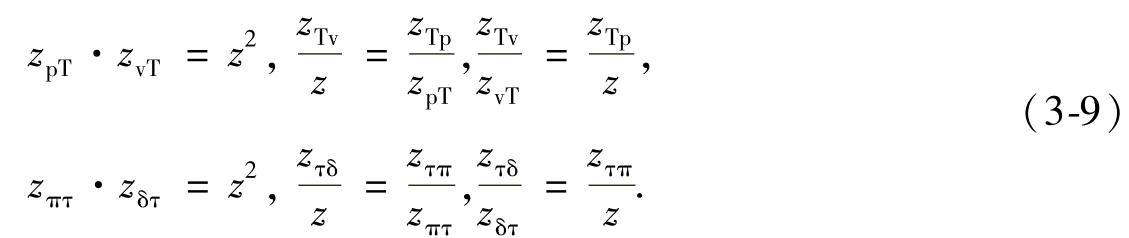
上述变换关系允许人们从特定的热力学方程和基本的状态方程（亥姆霍兹自由能源和吉布斯自由焓）中得到所有重要的偏导方程，并能变换成一个便于实际应用的方便形式。

基于这些给定关系式，可以轻易地找到计算热力学性能以及如声速a_s、等熵指数k_s、焦耳-汤姆逊系数μ_JT、泊松比γ和Grüneisen参数Φ等参数的合适形式。一些例子见表3-1（Gorski，1997；Gorski and Chmielniak，1993）。

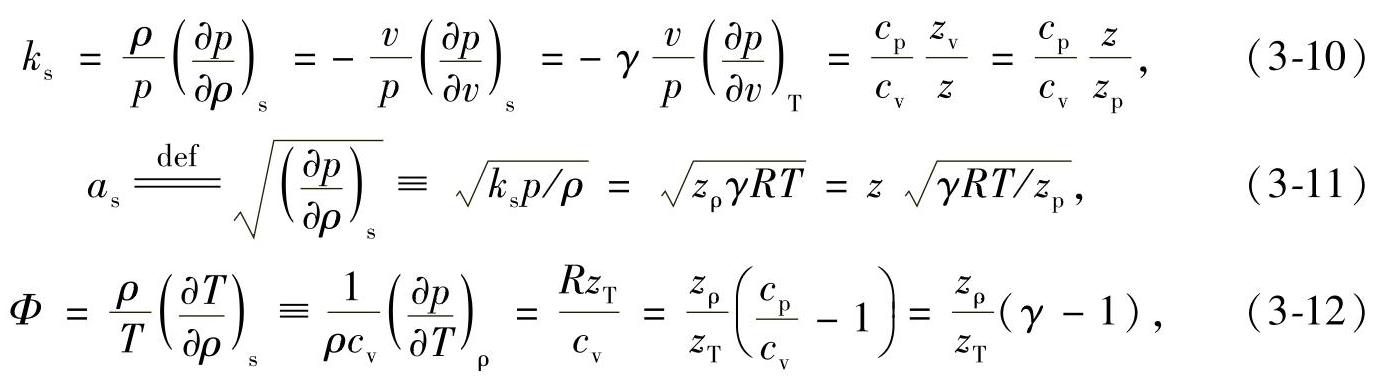
式中

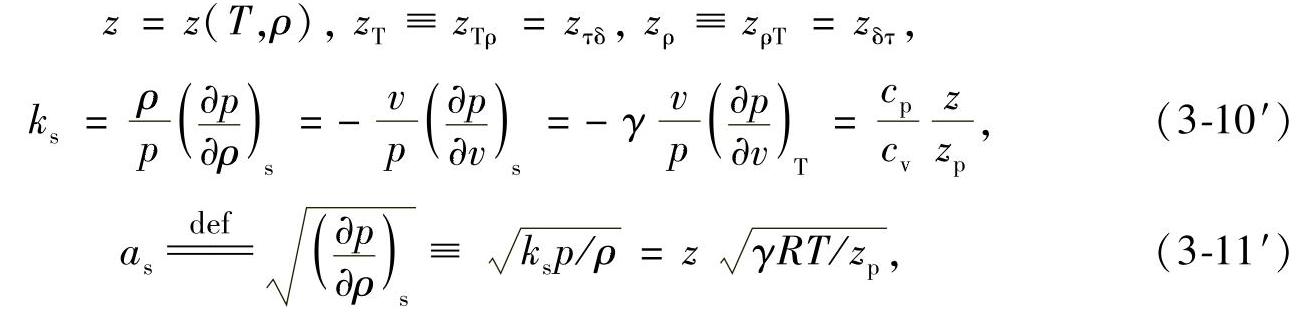
其中

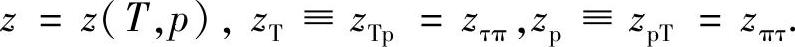
在表示重要物理参数与理想气体模型的差异时，这些恒等式都很简单。极限情况下有：若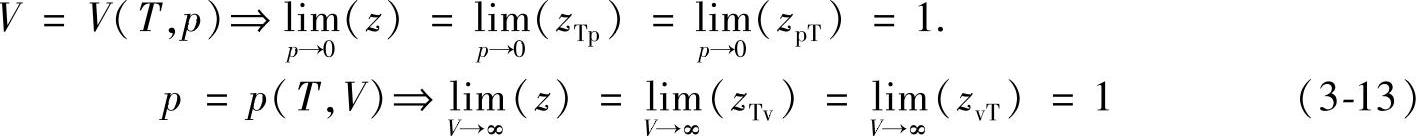及

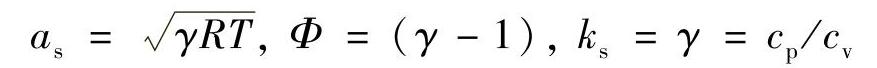
式（3-13）及其他上述关系式展示了实际与理想可压缩流体间差异的最简单、最合理的关系式。利用VCD方程可以获得额外的好处——可将不是由状态方程（EOS）推导出来的复杂数学关系式转化为另一个易于识别的符号形式，见表3-1。

亥姆霍兹自由能基本方程通常需要输入温度T和密度ρ来计算热力学性质。由于在技术应用上大多数情况下输入值不同，在单相流区以及汽液两相流区，工程上通过迭代（T，p），（T，h），（T，s），（p，ρ），（ρ，h），（ρ，s），（p，h），（p，s）和（h，s）的输入值来处理。

在其他所有性能特性完整的情况下，这些迭代可以计算出缺失的温度T和密度ρ（Bejan，2006）。近年来开发了大量的软件包（AspenTech公司，ChemicaLogic公司，Wagner和Overhoff，2006），使这些关于热力性能的简单的现代化计算方式为工业和科研用户所用。这些软件包为各种专用的领域应用所定制。