裂隙岩质边坡浸润线方程研究

由于裂隙岩体边坡中岩体岩性分布不一,裂隙等结构面随机分布且发育程度各异,岩体边坡中不同部位岩体性质可能存在较大差异,故裂隙岩体一般被视为复杂介质,此时为方便裂隙岩质边坡浸润线的研究,作如下基本假设:

(1)对称地存在两条完整切割潜水含水层的平行河流,河水位保持不变且沿河槽具有直立壁面;

(2)潜水含水层均质,各向异性,隔水底板水平不透水;

(3)入渗强度在空间上均匀分布,在时间上稳定;

(4)潜水流为二维稳定流,为方便计算引进裘布依假定,将问题降为一维流处理。

现先取单位渗流宽度的河间地段为对象进行研究,如图9.1所示。由于两河水位不等,存在分水岭,故以水均衡原理建立方程。

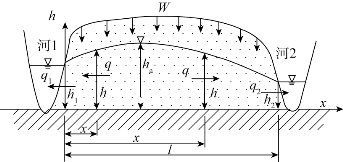
图9.1 有入渗补给的河间地段剖面

无论x在何处,均可得相同均衡式为

引入裘布依假定,取水力坡度方向上的渗透系数为KJ,则有

分离变量,由断面1至断面x积分,得

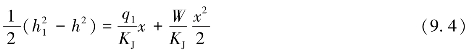
当x=l时,h=h2,则上式可写为(www.xing528.com)

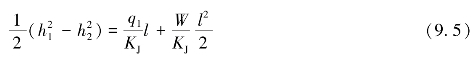
可得单宽流量方程为

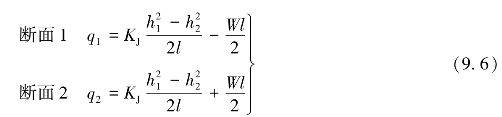
任意断面处的单宽流量方程为

将式(9.6)代入式(9.4),可得浸润线方程为

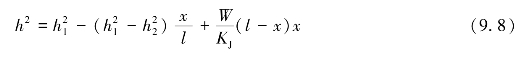
对式(9.8)分析可知,当W=0,即无入渗补给时,浸润线方程只是少了一项x)x,则可认为降雨入渗对地下水位的抬高主要由这一项决定。且当x=l/2时,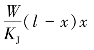能够取到最大值,即河间地段中间断面水位抬高最大。

现以图9.2岩体边坡为例,此时的h2已经不再表示河流水位高度,表示的是河间山体任意位置处的地下水位高度,且该值随着降雨入渗发生改变。获取h2的值有助于另一个水位点的选择。现假设两条河流距离L,h2所在的位置为l,则可根据两者的关系对式(9.7)进行修正。

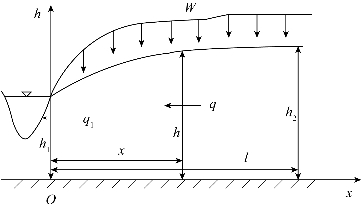
图9.2 边坡降雨入渗示意

修正后的浸润线方程可表示为

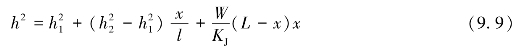
上列各式中,当水力坡度接近水平时,水力坡度方向上的渗透系数可近似取横向渗透系数。