基于隧道的DDA渗流作用分析优化方案

本节主要通过计算渗流的作用,讨论裂隙岩体和衬砌相互作用的情况下衬砌应力和应变的变化情况,从而分析渗流作用对隧道稳定性的影响。

图6.9和图6.10为DDA方法计算过程的时程曲线,曲线波动趋于平衡的点即为计算结果的取值点。

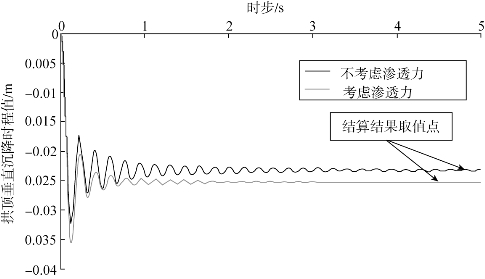
图6.9 隧道拱顶垂直沉降时程曲线(工况1)

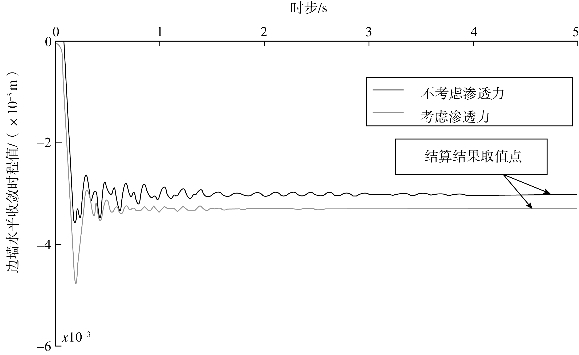
图6.10 隧道边墙水平收敛时程曲线(工况1)

分析过程中,将衬砌应力以柱状图表示,角度为0°代表隧道拱顶位置,顺时针为正,逆时针为负。比较图6.11和图6.12可知,裂隙岩体中隧道衬砌的最大法向应力值取决于不连续面的倾斜角度(倾角),倾角θ越大,最大法向应力值越大,反之越小。对于图6.8(b)的不连续面小倾角工况,渗透力对拱顶附近的衬砌应力有较为明显的影响,而对于图6.8(a)的大倾角工况,渗透力对拱顶及仰拱附近衬砌应力的影响都比较明显。

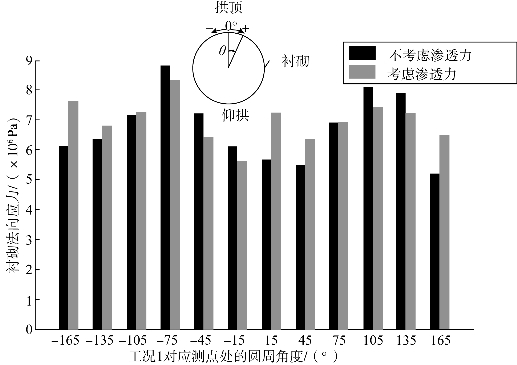
图6.11 工况1中衬砌最大主应力

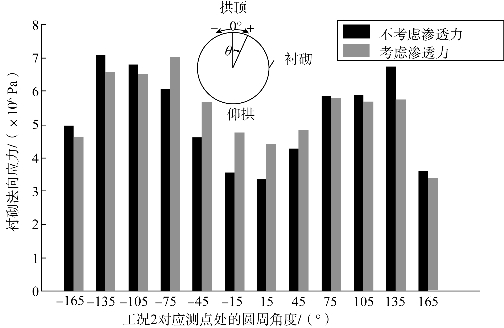
图6.12 工况2中衬砌最大主应力

根据图6.13和图6.14可知,埋置在大倾角裂隙岩体中的隧道衬砌垂直沉降和水平收敛较大。如图6.14所示,不连续面的倾斜角度对水平收敛的影响更为突出。通过以上分析可以看出,不连续面倾角和渗透力对围岩和衬砌之间的相互作用,都起到了明显的影响,但不连续面倾角对围岩稳定性的影响起到了控制性的作用。

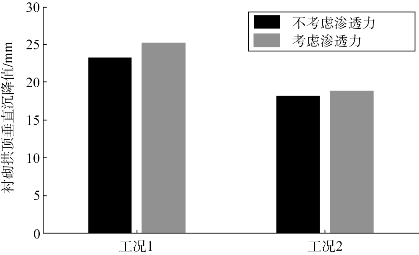(www.xing528.com)

图6.13 不同工况下隧道拱顶垂直沉降

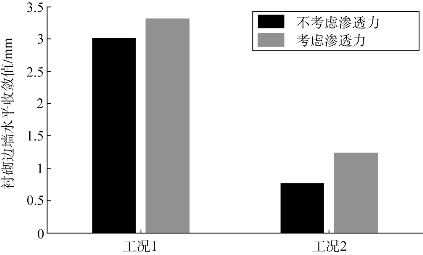
图6.14 不同工况下隧道边墙水平收敛

图6.15和图6.16显示了不连续面和渗透力对隧道垂直沉降和水平收敛的影响。从这两图中可以看到,不连续面倾角越大,渗透力和不连续面对围岩变形的影响越明显,但不连续面对隧道变形的影响起控制性作用。

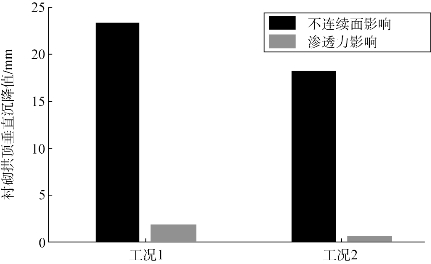
图6.15 不连续面和渗透力对隧道垂直沉降的影响

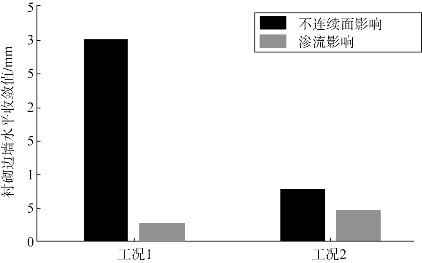
图6.16 不连续面和渗透力对水平收敛的影响

图6.17和图6.18展示了两种工况下围岩的破坏模型,从这两图中可以看出,倾角越大,隧道围岩的破坏越严重,而渗流作用(即渗透力)的存在,加剧了围岩的破坏程度;渗流作用对围岩破坏程度的影响,随着不连续面的不利组合程度的增大而增强。

图6.17 工况1的破坏模型

图6.18 工况2的破坏模型