渗流解析解的推导方法

由于开挖等原因,使得隧道周边围岩受到扰动,改变了其本来的渗流特性。为了研究扰动区围岩对围岩整个渗流特性的影响,本节假设了如图6.5所示的半平面渗流模型。在图6.5中,x轴方向表示地层表面,r1为隧道半径,r2为扰动区外半径,γ1和k1为扰动区围岩的重度和渗透率,γ2和k2为原岩的重度和渗透率,h为隧道的埋深,H为地表总水头,隧道周边存在常水头ha。

图6.5 半平面渗流模型

本节的理论研究主要采用共形投影方法,假设实际工况的扰动区围岩在复平面(共形投影平面)上的投影如图6.6所示。α1对应于半平面中的隧道圆周的投影半径,α2对应于半平面中的扰动区外边界圆环的投影半径,半径为1的圆环对应半平面的地层表面水平线。另外,投影平面内的扰动区圆环还原到半平面内并不是如图6.5所示的扰动区圆环,而是比实际扰动区域大,即拱顶部分与扰动区边界重合,仰拱以下部分比假设的图6.5所示扰动区域面积要大,所以本节推导得来的解析解的定义域始终包含了图6.5所示的扰动区域,在应用本节的解析解进行实际工况的渗流讨论时,实际的渗流区域始终在有效的定义域内,计算结果总是合理的。

将图6.5所示的半平面投影到如图6.6所示的复平面上的投影方程为

图6.6 共形投影平面

α1和α2定义为

从式(6.73)、(6.74)可以看出,α1和α2仅与隧道的相对埋深有关。根据式(6.72),引入复数势函数,即

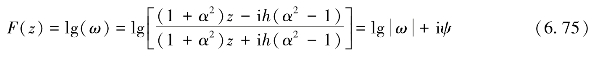
令

因此围岩中的总水头分布方程可表示为

式(6.77)、(6.78)中:C1、C2、C3和C4为常数;h1和h2分别代表扰动区围岩和原岩的总水头分布函数。根据半平面内的边界条件,可得下列方程。

在水平地层表面有

在隧道表面有

在扰动区外边界处有

在复平面内,沿任意同心圆圆周的流量都相等,令沿隧道周边的流量为Q1,沿扰动区外边界的流量为Q2,则根据流量守恒,可得如下方程,即(www.xing528.com)

假设沿各边界的流速分别为q1和q2,根据达西定律,流速q1和q2可分别表示为

因此流量Q1和Q2可表示为

∂A1和∂A2分别表示隧道圆周x2+(y-h)2=和扰动区外边界圆周x2+(y-h)2=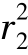;根据高斯散度定理可得

A1和A2分别表示隧道断面面积x2+(y-h)2≤和扰动区外边界包围的断面面积x2+(y-h)2≤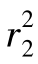。将式(6.76)和式(6.77)代入式(6.83)、(6.84)中,则有

又著名的方程其中,因此,有

由式(6.78)、(6.85)、(6.86)、(6.87)、(6.88)可得

由以上各边界条件和式(6.89),可求得常数C1、C2、C3和C4分别为

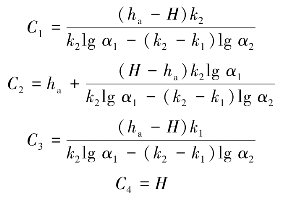
围岩总水头分布函数可表示为

如果α1=α2,k1=k2,则式(6.90)和式(6.91)为同一方程,此时表示围岩中不考虑扰动区的影响,围岩为均一介质。

将总水头分布函数用极坐标表示,即x=ρcos θ,y=ρsin θ-h,此时可求得围岩中的径向水力梯度表达式,即

iρ1和iρ2分别表示扰动区内和扰动区外的围岩内径向水力梯度,它们进一步求解后的表达式分别为