DDA方法的理论基础详解

DDA方法是用来模拟具有离散块体的岩土材料的一种数值方法,该方法由石根华和Goodman提出,其他研究者在此基础上也进行了深入研究。DDA方法既借鉴了FEM在计算应力和变形的特点,又吸取了DEM在处理破碎块体系统和块体接触方面的优点,因此DDA方法在很多方面具有优点。DDA方法应用闭合积分生成刚度矩阵,同时为单元平衡方程或运动方程赋予矢量计算,计算过程中遵循如FEM中的总能量最低原则。在块体接触方面,DDA方法采用了包括块体嵌入接触的诊断法用以满足非嵌入要求。另外,Tomofumi等还将摩尔-库伦准则应用于判断块体接触面摩擦强度的问题。

1.变形矩阵

每一个块体,每一步变形过程中将其应力、应变看成常数,应用线性近似原理,块体中任意一点的位移矩阵可以通过对应位置及位移向量D得到。位移向量由6个位移分量组成,即

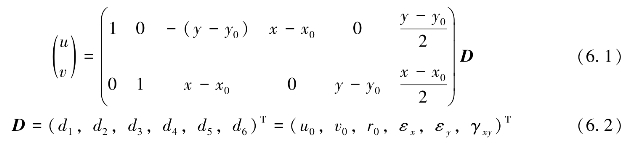
式中:(x0,y0)为块体质心坐标;u0、v0和r0分别表示直角坐标系中沿x、y轴方向的平动和沿一定弧向的刚体转动;εx、εy和γxy分别为沿x、y轴方向的正应变、块体的剪应变。

2.控制方程

总能量Π由块体系统中几部分能量之和组成,其中下标表示块体系统中的不同部分,总能量表达式为

式中:Πp为点荷载产生的能量;Πl为线荷载产生的能量;Πw为体荷载产生的能量;Πi为惯性荷载产生的能量;Πσ为主应力产生的能量;Πe为弹性应变产生的能量;Πv为黏聚力产生的能量;Πm为固定点外力产生的能量;Πc为连接力产生的能量。

对总能量求最小值,根据位移向量D,控制方程可写为

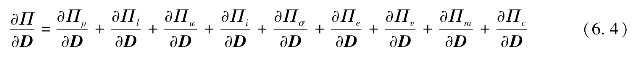
从式(6.4)可以得出,每一个块体都可用一个局部平衡方程来描述,并可用其来描述块体系统的移动,而不同点在于采用独立的能量原理。因此,这些局部方程可以跟FEM一样,组装成整体方程。

3.点荷载

作用在第i个块体上坐标为(x,y)点上的点荷载用(Fx,Fy)表示,因此第i个块体(见图6.1)上点(x,y)的位移(u,v)为

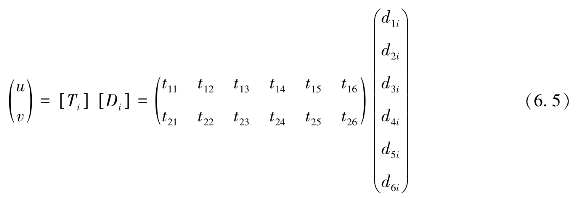
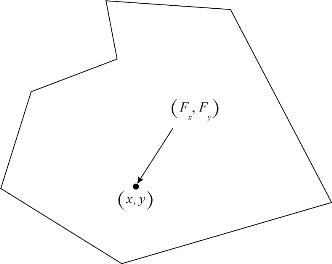
图6.1 点荷载

点荷载(Fx,Fy)产生的势能可表示为

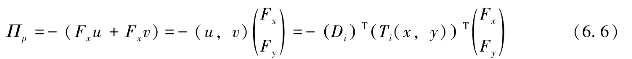
对Πp求最小值得

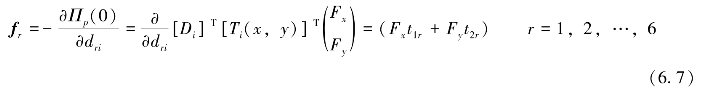
fr(r=1,2,…,6)可形成6×1的子矩阵,即

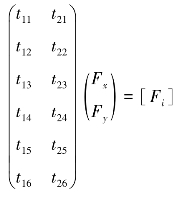
此处的[Fi]为6×2和2×1的两个矩阵之积。

4.线荷载

假设荷载沿点(x1,y1)到点(x2,y2)之间呈线性分布,如图6.2所示,线荷载方程可表示为

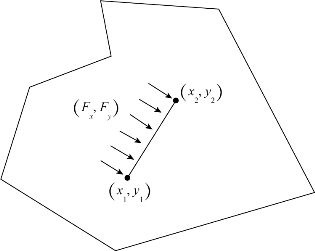
图6.2 线荷载

线段长度可表示为

设荷载为

沿加载线变化,线荷载(Fx(t),Fy(t))产生的势能可表示为

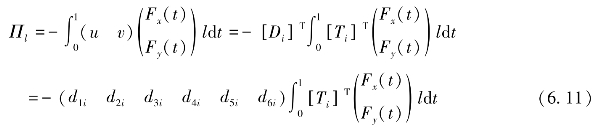
对Πl求最小值得

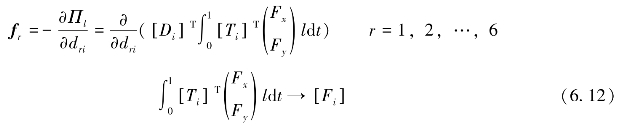
此处的[Fi]为6×2和2×1的两个矩阵之积。

5.体荷载

假设fx、fy是作用在第i个块体上的恒定体积力,而且x0、y0为第i个块体的重心坐标,因此

由此可得

恒定体积力fx、fy产生的势能为

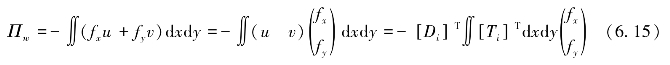
由于

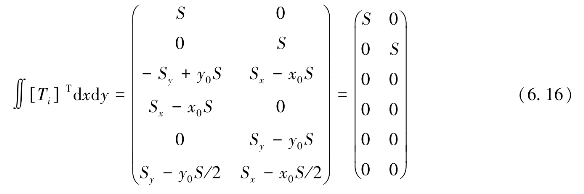
根据式(6.14),因为x0、y0是块体重心坐标,所以式(6.16)最后四行为0,即

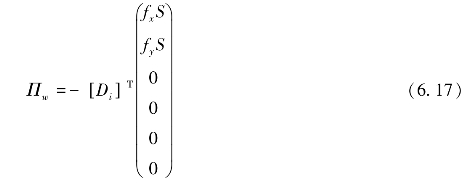
对势能求导并取最小值,得

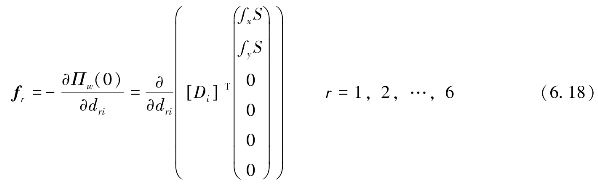
fr(r=1,2,…,6)可以形成一个6×1的矩阵,即

6.初始荷载

对于第i个块体,初始恒定应力所产生的势能为

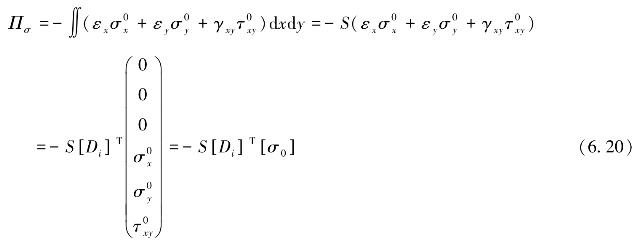
对第i个块体的整个表面积进行积分,S为面积。通过求导,对Πσ取最小值得

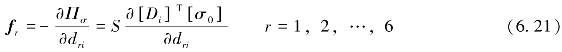
fr是一个6×1矩阵,即

7.弹性应力

由第i个块体的弹性应力产生的弹性应变能为

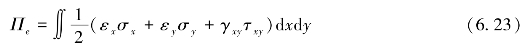
式(6.23)对第i个块体的整个表面积进行积分,对于每一个位移,假设块体为线弹性体,因此,在平面应力情况下有

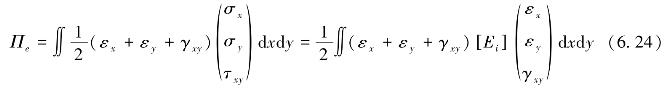
即

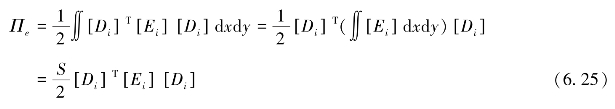
S为第i个块体的表面积,求导,并对弹性应变能Πe取最小值得

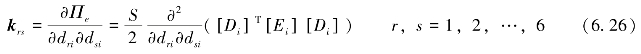
krs为6×6矩阵,即

8.惯性荷载

单位面积上的惯性荷载表达式为

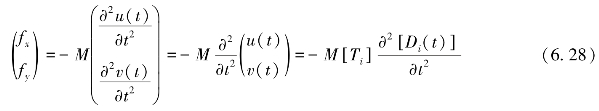(www.xing528.com)

式中:(u(t),v(t))表示第i个块体中对应于点(x,y)且与时间有关的位移值。从而,第i个块体的惯性荷载产生的势能可表示为

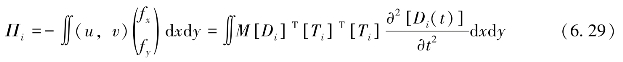
如果用Δ作为时间增量,对时间进行积分可得

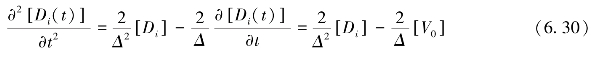
V0是计算时步中的初始变形速度,可得

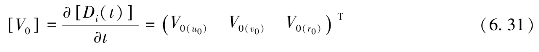
因此,惯性荷载产生的势能可表示为

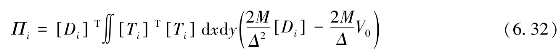
惯性荷载产生的势能对位移求导,得

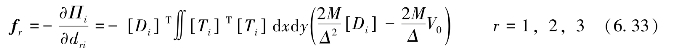
fr为6×1矩阵,即

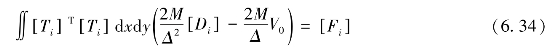
式(6.34)中的[Di]为未知矩阵,因此,该式可以转化为以下两式,即

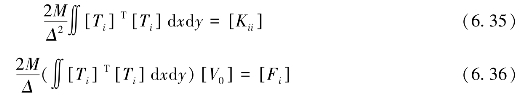
9.黏聚力

由于岩块之间的黏结作用产生的抗力与块体移动速度和块体表面积成正比,因此当每个单位时间的位移增量被给定时,黏聚力可表示为

式中:Δ为时步;η为黏度;u、v为单位时间的位移增量。第i个块体由黏聚力产生的势能为

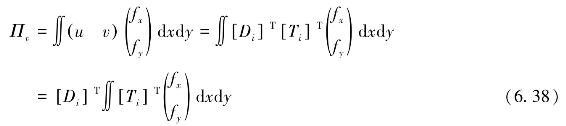
黏聚力也可以当作体积力来处理。为了达到平衡,Πv对位移变量取最小值得

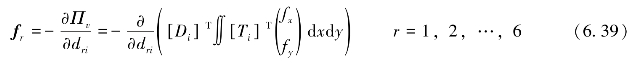
fr为一个6×1矩阵,同时可得

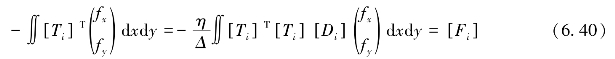
10.约束节点力

某些块体被固定在特定的点上作为边界条件,而约束就是在块体系统中用刚度非常大的弹簧来实现。假设固定点为第i个块体上的(x,y),则位移可表示为

若计算位移用(u,v)表示,沿x和y方向分别用弹簧连接,弹簧的刚度用p表示,则约束节点力可表示为

因此,约束节点力产生的弹性势能Πm可表示为

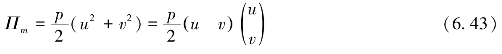
由于

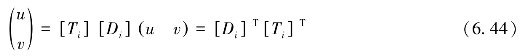
则Πm可表示为

对Πm求导并取最小值得

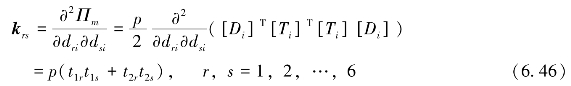
krs为6×1矩阵,即

11.连接力

假设用锚杆或连杆连接第i个块体的点(x1,y1)和第j个块体的点(x2,y2),连接点不一定是块体的顶点,则锚杆端点的位移可表示为

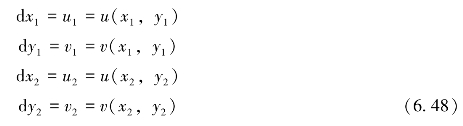
锚杆的长度可表示为

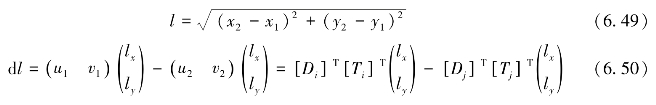
此处

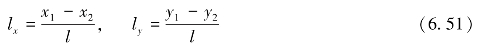
为锚杆的方向余弦。

假设锚杆的刚度为s,则锚杆的连接力可表示为

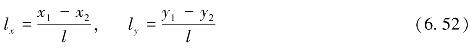
锚杆连接力产生的弹性应变能可表示为

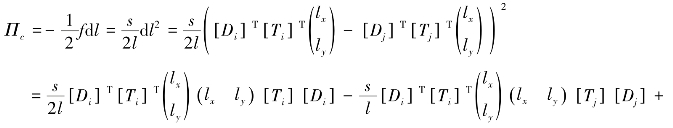
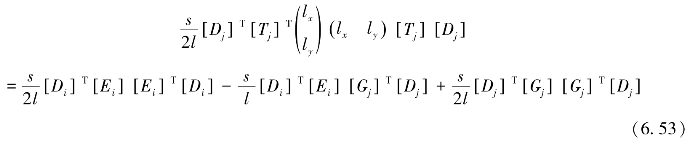
此处

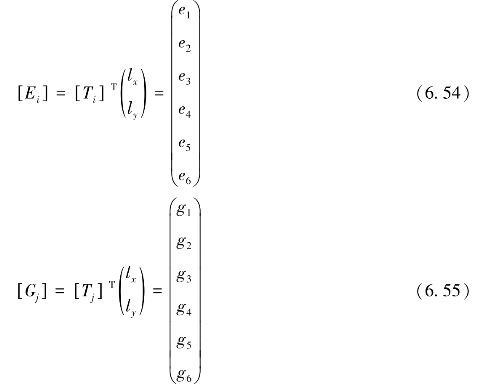
对Πc求导得

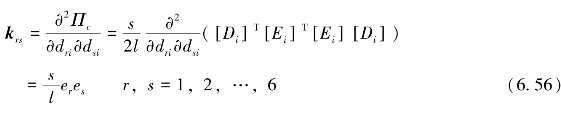
由此可得6×6矩阵,即

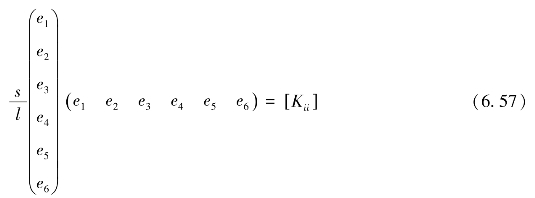
可将式(6.57)代入整体方程的子矩阵[Kii]中,得

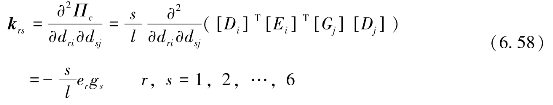
由此可得6×6矩阵,即

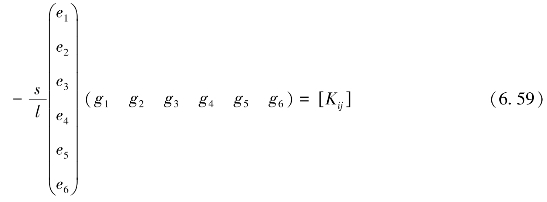
可将此矩阵代入整体方程的子矩阵[Kij]中,得

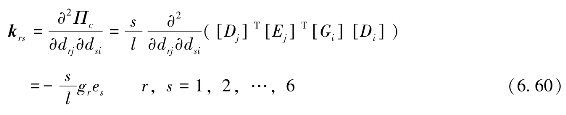
可得6×6矩阵,即

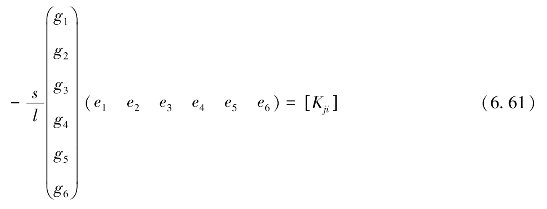
将此矩阵代入整体方程中的子矩阵[Kji]中,得

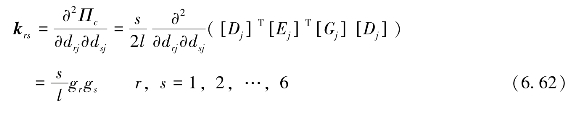
可得6×6矩阵,即

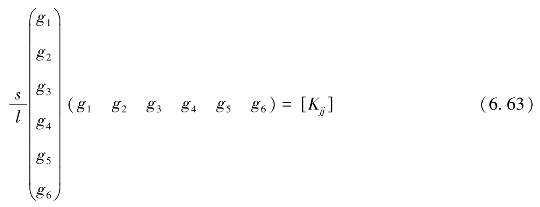
将此矩阵代入整体方程的子矩阵[Kjj]中。

12.整体方程

块体之间的接触及块体边界位移约束将独立块体形成了块体系统。假设在定义的块体系统中有n个块体,则建立联立的平衡方程为

在式(6.64)给出的每个单位系数矩阵中,由于块体有6个自由度(u0,v0,r0,εx,εy,γxy),因此式(6.64)是6×6矩阵。[Di]和[Fi]是6×1矩阵。其中,[Di]表示第i个块体的位移变量(d1i,d2i,d3i,d4i,d5i,d6i),[Fi]表示加载到第i个块体上且分别沿6个位移分量方向的荷载矩阵。子矩阵[Kii]取决于第i个块体的材料特性和矩阵[Kij ]。i≠ji≠j是由第i个块体与第j个块体之间的接触决定的。平衡方程由应力和荷载产生的总能量Π取最小值得到。