非平行裂隙水头分布公式推导

当岩体裂隙各点应力变化不同或由于物质充填、溶蚀,其裂隙的隙宽也将发生变化,沿着流体流动方向,裂隙将会形成3种形式,第一种为扩散型裂隙,如图3.20所示;第二种则为收缩型裂隙,如图3.21所示;第三种为上述研究的平行裂隙,裂隙仍保持平行。

图3.20 扩散型裂隙

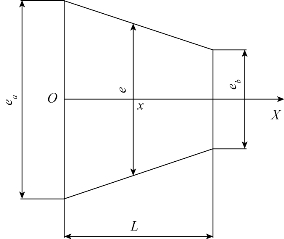
图3.21 收缩型裂隙

设流体沿X轴方向流动,对于扩散型裂隙(见图3.20),假设裂隙长度为L;左边宽度为ea,其水头(也称水压力)为H0;右边宽度为eb,其水头为HL;裂隙任一点处的稳定流量为Q;裂隙隙宽为e;则根据立方定律可得

式中:γ为流体的相对密度,η为流体的黏度。

于是有

假设,则式(3.72)变为

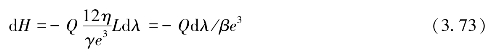
式中:。

假设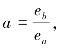a>1,对于任一点x处,其隙宽为

从式(3.73)可知,水头H是λ的函数,则可以表示为H=H(λ)。

当λ=0时,则有H0=H(0);当λ=1时,则有HL=H(1)。

对式(3.73)左右两侧同时积分,则任意点处的水头为

则在x处的流量为

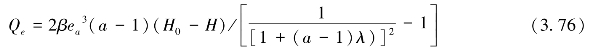
在出口处eb的流量为

由质量守恒定律可知,Qe=Qeb,则有

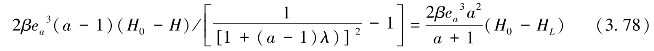
则在任意点处的水头为

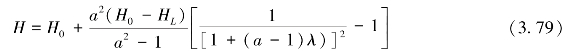
对于该过程的单宽裂隙压力则有

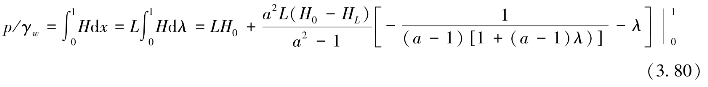(www.xing528.com)

对式(3.80)求积,则压力p可表示为

式中:γw为水的单位重度。

对于收缩型裂隙,其裂隙情况与扩散型裂隙恰好相反。此时,流体的流向仍沿X方向进行流动。对于该种情况(见图3.21),仍假设裂隙长度为L;左边宽度为ea,其水头为H0;右边宽度为eb,其水头为HL;裂隙任一点处的流量为Q;裂隙隙宽为e。则根据扩散型裂隙的推导过程,可以得到收缩型裂隙的水头分布公式,以及在流动过程中的压力表达式为

单宽裂隙压力表达式为

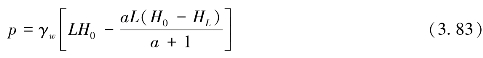
可以看出,式(3.82)与式(3.79)、式(3.83)与式(3.81)具有相同的表达形式,唯一不同的是对于收缩型裂隙,表达式中的a与扩散型裂隙相反,其中

对于以上的推导,可用以下例题进行验证。

[例题] 裂隙的水力学参数为:左侧的水头值为恒定值,H0=0.8 m;流体只能在裂隙中流动,岩块为不透水边界;右侧也为恒定的水头值,HL=0.4 m;裂隙长度L为L=0.14 m。根据上述的参数,请分别对扩散型裂隙和收缩型裂隙这两种情况进行分析。

解:对于扩散型裂隙,取a=2,则裂隙中的水头分布曲线如图3.22所示。图3.23为平行裂隙的水头分布曲线,两者对比,可以发现,对于扩散型裂隙其水头分布曲线处在平行裂隙水头分布曲线的下方,这说明扩散型裂隙中任意一点的水头均小于平行裂隙与该点对应的同一点处的水头(除了裂隙的两端点)。

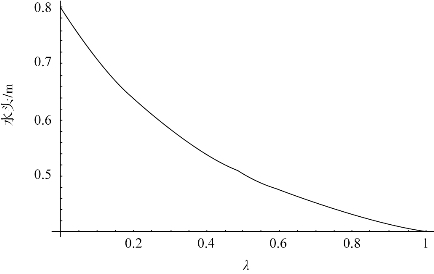
图3.22 扩散型裂隙水头分布曲线

对于收缩型裂隙来说,取a=0.5,则裂隙中的水头分布曲线如图3.24所示,与图3.23相比,可知收缩型裂隙中任意一点的水头均高于平行裂隙中与该点对应的同一点处的水头(除了裂隙的两端点)。也就是说,在该过程中,流体具有较高的压力。

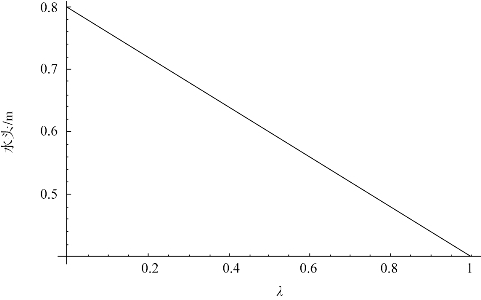
图3.23 平行裂隙水头分布曲线

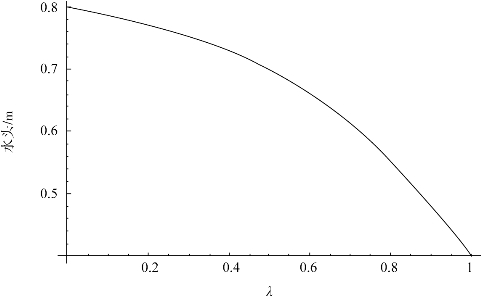
图3.24 收缩型裂隙水头分布曲线

当a取不同值时,裂隙水头分布也不相同。

对于扩散型裂隙,取a为2～10,图3.25为该种情况的水头分布曲线。从图中可以看出,随着a值的增大,裂隙中水头下降,水头曲线下凹越大,水头曲线的曲率越大。可以认为,水头曲线与λ轴所围成的面积即为流体在流过裂隙时所具有的压力,亦即随着a值的增加,流体在流经裂隙时,其所具有的压力越低。

图3.25 扩散型裂隙不同a值的水头分布曲线

对于收缩型裂隙来说,取a为图3.26是该种情况的水头分布,从图中可以看出,随着a值的减小,裂隙中水头下降,水头曲线越凸,水头曲线的曲率越大。可以认为,水头曲线与λ轴所围成的面积即为流体在流过裂隙时所具有的压力,亦即随着a值的降低,流体在流经裂隙时,其所具有的压力越高。因此,可以认为本书得到的公式对于扩散型裂隙与收缩型裂隙水头分布的预测较为理想。

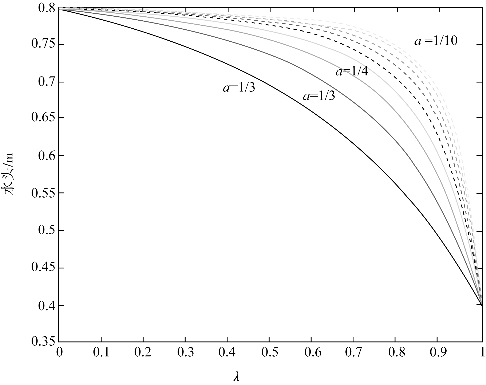
图3.26 收缩型裂隙不同a值的水头分布

对于扩散型裂隙(a=2)来说,流体在流动过程中,其具有的水头较低,使得流体在整个流动过程中所具有的压力最小;对于收缩型裂隙(a=0.5)来说,流体在流动过程中,其所具有的水头较高,使得流体在整个流动过程中所具有的压力较大。3种不同裂隙形式的单宽裂隙中流体压力比较如表3.1所示。

表3.1 3种不同裂隙形式的单宽裂隙中流体压力比较