立方定理的推导方法

假设水是不能压缩的,则流体的连续方程为

对于平面二维问题,如图3.17所示,上式变为

图3.17 二维单裂隙水流示意

于是流体运动方程的微分可表示为

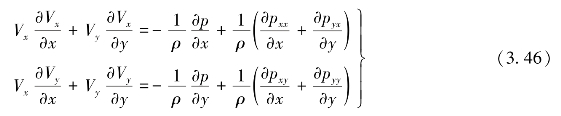
又由于裂隙隙宽相对很小,因此水流可视为沿x方向流动,即Vy≈0

则式(3.46)变为

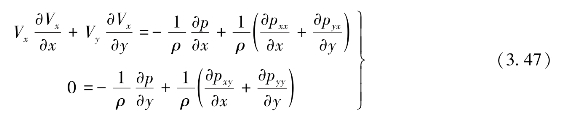
又由牛顿切应力公式知

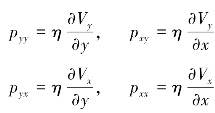
同时,由于Vy≈0,可得将其代入式(3.45),则可得

将式(3.45)与式(3.47)结合,则得沿裂隙的水流方程为

由于流体黏度η与坐标无关,所以式(3.49)变为

单裂隙水流的边界条件为(www.xing528.com)

对式(3.50)进行二次积分,可得

将边界条件式(3.51)代入式(3.52),则可以解得

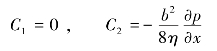
将代入式(3.52)中,则可以得到

令水流压力梯度又由于p=γ(H-Z),则

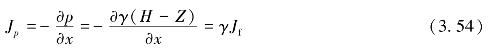
将式(3.54)代入式(3.53)中,则式(3.53)变为

式中:Jf裂隙中的水力梯度,γ为水的相对密度。

当y=0时,即沿裂隙中心轴线上流速最大,其值为

因此,通过裂隙断面的单宽流量为

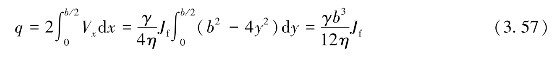
式(3.57)就是光滑、平行裂隙的立方定律。从公式中可以看到,裂隙的单宽流量与裂隙隙宽的立方成正比。但是实际的岩体的裂隙的渗流受到很多因素的影响,如裂隙的粗糙度、裂隙的充填度,以及岩体所处的应力状态。因此,对于不同粗糙程度的裂隙水流问题,有许多修正公式。在低应力时,裂隙的绝对粗糙度要小许多,因此裂隙渗流接近于平行板模型,其测量结果与光滑裂隙渗流公式计算结果基本吻合,裂隙岩体的渗流变化,主要与岩体裂隙的变形有关。

对于立方定律的适用范围许多人进行了研究。Witherspoon等在法向应力作用下大理岩裂隙渗流研究的基础上,得出了如图3.18所示的规律。

图3.18 流量与等效隙宽的关系