渗流-应力耦合模型的优化方案

岩体由于其自身的特点,使得岩体的应力渗流特性与土体有着本质的区别。由于成岩作用及成岩环境的差异造就了岩体的物质基础和宏观结构,以及微观结构上的非均质性、各向异性和不连续性,从而导致了岩体整体力学性质与岩石块体的不同,如岩体强度的弱化及渗流的复杂性。岩体卸荷后,将会在岩体中形成卸荷裂隙,岩体中卸荷裂隙的生成,使得岩体中裂隙扩展,初始闭合的裂隙将会张开,形成水渗流的通道。一些研究者倾向于认为:当裂隙网络由多组裂隙构成,裂隙间距与分析尺寸相比甚小时,可用连续介质理论研究裂隙岩体渗流。目前,对于岩体渗流的数学模型主要有以下几种:①等效连续介质模型;②离散裂隙网络模型;③双重介质模型。对于不同的岩体结构形式,采用不同的计算方法,如图3.15所示。

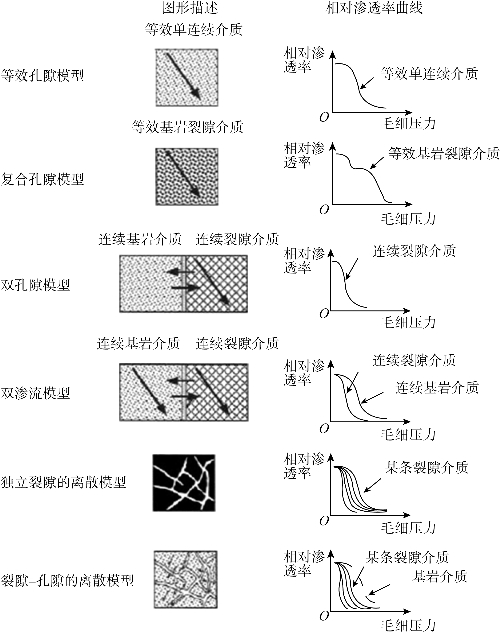
图3.15 裂隙岩体渗流模型及其相对渗透率曲线

1.等效连续介质模型

等效连续介质模型是把研究的对象看作是无间隙的连续介质,岩体介质中的空隙相互连通,水流充满了整个岩体介质。当岩体的孔隙度较大时,该模型认为岩石的孔隙介质和裂隙网络均匀分布于整个计算域内,裂隙岩体表现出与多孔连续介质相似的渗透特性,水位随空间连续分布。渗流场的求解以渗透张量为基础。该模型假定地下水在岩体中的流动服从Darcy定律,渗透系数为岩体单元的平均值。Oda(1986)基于两个假定:①裂隙为弹性连续体;②每一裂隙由平行板组成,提出了渗流与应力耦合作用的等效连续渗流模型。Franklin(1991)在考虑各向异性渗透张量及应力和节理闭合的重要影响时,认为上述假定是可信的。但在等效连续介质模型中,对于单一裂隙,则3种情况必须予以考虑:①如断层那样的主要导水管道;②基于裂隙特性而非实测资料来预测岩体的渗透特性;③井周围裂隙网络的渗透系数很低,模拟水压断裂和油井注入。

2.离散裂隙网络模型

离散裂隙网络模型最初由wittke(1966)提出,后由Louis(1968)、Wilson和Witherspoon(1974)、王恩志(1991)等作了进一步的发展。岩体经历了长期的地质作用,产生了不同类型、不同力学性质和不同规模的节理、裂隙及断裂面,这种裂隙个体在空间上相互交叉,构成了离散裂隙网络模型,该种渗流模型具有非均质性和各向异性。同时,由于裂隙网络中阻水裂隙的存在,裂隙的连通性差,引起裂隙中水流断续分布,这些互不连通的裂隙或存在阻水裂隙的网络,称为非连通裂隙网络模型。由于裂隙网络模型中裂隙的隙宽大小差异,引起大部分水流集中在少数裂隙内,这正如田开铭教授通过室内试验证明的那样,他称这种现象为“裂隙水偏流效应”,该研究与Tsang的研究相一致。

根据切尔内绍夫的观点,把裂隙网络进行分类:依据裂隙定向排列的相互关系(排列的整齐程度及几何形状),把裂隙分为系统类裂隙网络、多角形类裂隙网络和混乱类裂隙网络。依据裂隙末端相互配置的性质和岩体受裂隙的切穿程度,又将裂隙网络分为连续型、断续型和片断型。在实际分布的岩体系统内,裂隙大多是构造裂隙,因而系统类裂隙网络在实际中出现很多。该类模型可以细分为以下4类。

(1)Monte-Carlo模型。由于实际岩体中裂隙网络的分布十分复杂,用人为调查方法无法描述岩体内裂隙的分布,因此只能采用统计的方法来进行分析,这种方法得到的模型就称为Monte-Carlo模型。建立Monte-Carlo模型的基本方法是在现场对裂隙进行抽样调查,取得裂隙指数的统计参数,再根据裂隙不同参数所服从的统计学规律,由计算机生成裂隙网络进行统计分析。该模型与实际情况具有统计学的等效性,但是对于三维问题,采用该种模型时的工作量太大,且迄今尚无有效手段进行解决。

(2)裂隙水力学模型。该模型把岩体渗流问题视为裂隙水力学问题。考虑到裂隙面的粗糙度及充填情况,对单一平行裂隙的流速进行修正,考虑裂隙面的粗糙度的修正系数。其渗透系数表述为(www.xing528.com)

式中:ρ为水的密度;g为重力加速度;e为裂隙开度;η为水的黏度;C为裂隙面粗糙度修正系数,对于该系数,不同的学者提出了不同的计算方法。

Lomize(1951)认为,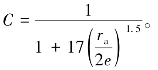

Louis(1969)认为,。

Eda F.de Quadros认为,。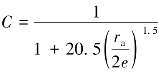

式中:ra为裂隙最宽处与最窄处的差值。

(3)典型裂隙面模型。该模型对实际岩体的结构面进行比较详细的统计分析,找出优势结构面,即可将实际岩体抽象为由该几组裂隙面所分割的岩体结构。自20世纪60年代以来,国外学者便开始了该类模型的研究,如Long(1985)将裂隙视为随机分布的圆盘;万力(1993)运用岩体中的大中型裂隙建立了裂隙网络渗流模型,假定裂隙为无限延伸的平面,岩体由其相互切割而呈多边形状。

(4)管道模型。该种模型是指以溶蚀管道相互交叉形成的管状网络含水介质,这种模型认为空间裂隙是由一系列平行圆管或相互交叉圆管所组成的,管道水流大多以层流为主。每一圆管的直径,也为结构面的开度,则总渗流量为每一管道渗流量总和。

3.双重介质模型

双重介质模型是由学者Barenblatt(1960)提出的,他把岩体看作由孔隙和裂隙组成的双重介质空隙结构,孔隙介质和裂隙介质均处于渗流区域内,形成连续介质系统,在该系统内,孔隙体积远大于裂隙的体积,而裂隙的导水性远高于孔隙的导水性,因此孔隙介质储水,裂隙介质导水。由于裂隙介质的导水作用,在双重介质模型内形成了两个水头,即孔隙介质中水头和裂隙介质中水头,基于Darcy定律分别建立两类介质的水流运动方程,这两种介质之间通过水流交换相联系。但是,该模型没有反映裂隙系统空间结构的不均匀性,以及其中水流普遍具有的各向异性,而且在同一点给出两个压力值是困难的,因此很多学者提出了自己的计算方法,如黎水泉、徐秉业(2000),提出了一种考虑介质参数随压力变化的双重介质非线性渗流模型,研究了孔隙水压力随着时间的变化规律。