岩体卸荷水力损伤机理深入探析

岩体工程在加荷与卸荷条件下,其力学特征有着本质的区别。在卸荷量较大时,岩体中结构面的力学条件将发生本质的变化。这些结构面将迅速劣化岩体质量,使其力学参数急剧下降,并发生卸荷损伤,而在力学上岩体将经历的过程为:岩体工程开挖—应力释放—岩体损伤—岩体变形。因此,岩体变形导致结构面连通率增加,结构面开度加大,岩体发生损伤。当岩体处于地下没有受到扰动时,其处于一定的原始地应力场与地下水压力的共同作用中。初始地应力在裂隙面的法向分量,促使裂隙面有压缩闭合的趋势。岩体作为地下水的通道及赋存体,地下水压力在裂隙面上的法向压力将促使裂隙张开。随着工程的开挖卸荷,如隧道、边坡等,与初始地应力场相比,岩体应力分布将发生较大的变化。根据裂隙与卸荷面空间位置的不同,岩体中将会发生卸荷损伤,如图3.5所示,其开挖卸荷面均与Z轴垂直。

图3.5 卸荷损伤的3种典型模式

(a)张开型损伤;(b)滑移型损伤;(c)撕开型损伤

根据裂隙的产状与开挖卸荷面的空间位置,上述3种典型的损伤模式均有可能存在。对于图3.5(a)的张开型损伤,其进行简化变为平面问题后,可建立坐标系如图3.6所示,则平面内的应力分布为

式中:KI为I型裂隙强度因子,。

图3.6 Ⅰ型裂隙

图3.5(b)中的损伤模式为纯剪切的状态,将其简化为平面问题后,建立坐标系如图3.7所示,应力分布为

式中:KII为II型裂隙强度因子,τ为剪应力。

图3.7 Ⅱ型裂隙

图3.5(c)中的损伤模式也是一种纯剪切状态,裂隙沿着Z轴方向前后错开,建立坐标系如图3.8所示,应力分布为

式中:KIII为III型裂隙强度因子,,τ为剪应力。

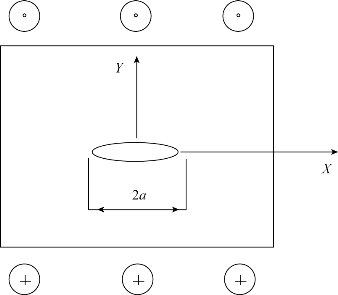
图3.8 Ⅲ型裂隙

1.岩体卸荷损伤的等效准则

随着岩土工程的发展,岩体的评价方法也得到了较快的发展。目前岩体评价方法主要有RMR法、Q值法、GSI法等。由于采用的参数不同,不同的岩体评价方法具有不同的优缺点。因此,Hoek提出了GSI(Geological Strength Index)岩体评价方法(简称GSI法),该法考虑了工程对于岩体的扰动效应,对于扰动过的岩体稳定性评价较为准确。由于节理在岩体中是普遍存在的,所以对于裂隙岩体,Hoek等提出的破坏准则为

式中:mb为裂隙岩体材料的Hoek-Brown常数;s、a为与岩体材料相联系的常数;σ1为破坏时最大主应力;σ3为破坏时最小主应力;σci为完整岩石的抗压强度。

式中:D为扰动系数,与开挖卸荷导致的应力释放和损伤有密切联系。对于没有扰动的岩体来说,D=0;对于扰动很大的岩体,D=1;对于其他情况,其值在0～1之间。

对于平面问题,假设在卸荷岩体中只存在两种损伤模式,即张开型损伤和滑移型损伤,这两种损伤均有可能发生,因此根据叠加原理,岩体的应力分布为

式中:r为缝端某点与水平轴的距离;θ1、θ2为缝端某点与水平轴的夹角。

又由于

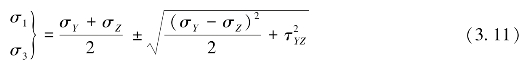
把式(3.11)代入式(3.6)中,并化简,则有

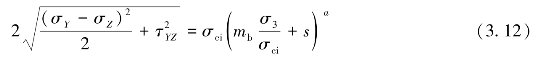
将式(3.7)、(3.8)、(3.9)、(3.10)代入式(3.13)中,则有

式中且A=KIsinθ1sin。,σY+σZ=为岩石材料的Hoek-Brown常数。

由于θ1=θ2,因此当θ1=90℃时,则式(3.13)变为

式(3.14)即为岩体开挖卸荷后,岩体地质力学参数GSI与裂纹强度因子K之间的关系,是一个岩体分类的等效关系式。

2.穿透型裂隙岩体的卸荷损伤

1)法向水压力作用下穿透型裂隙卸荷损伤的裂纹强度因子

在卸荷过程中,饱和岩体裂隙中存在的水压力将会对裂隙面上的每一点形成一个均匀的压力荷载,在这种水压力作用下,裂隙将会有一种张开的趋势,这与张开型损伤相符合。由弹性断裂力学原理知,当几个荷载同时作用在一个物体上时,则荷载组在某一点引起的应力和位移等于各个单个荷载在该点处引起的应力和位移分量之和。对于裂隙中有水压力存在的情况,可以采用叠加原理来进行处理,如图3.9所示,其中裂隙中的水压力是p。图3.9(a)可以看成是由图3.9(b)、(c)、(d)叠加而成的,图3.9(b)可以看成是一个受到双向压力作用下的无裂隙的压力平板,故其裂纹强度因子是0。对于图3.9(c)所示的裂隙的应力分布可由式(3.3)表示。对于图3.9(d)所示的情况,可根据断裂力学原理,对其进行求解。假设在裂隙壁面上某点存在一对集中力q,该力与裂隙中心相距b,且b<a(a为裂隙的宽度),则有

图3.9 应力场叠加原理

式(3.15)的参数意义与前文相同。根据式(3.15),由叠加原理可知,当均布荷载只在x=±a1范围内存在时,a1<a,取微段db,则在db上受到的载荷为pdb,可看成集中力,则用pdb代替式(3.15)中的q,并利用叠加原理可得

在式(3.16)中,令b=asin θ,则有,db=acos θ·dθ,代入式(3.16)积分后,可得

当p在整个裂隙表面均存在时,也就是说,水压力均匀地分布在裂隙的整个表面,这时,只要用a来替代式(3.17)中的a1,即可得到充满水的裂隙中的裂纹强度因子的值,即

式(3.18)为不考虑卸荷应力场,仅仅考虑裂隙水压力对裂隙的作用时,所得到的裂纹强度因子。

在卸荷过程中,当裂隙中充满水时,裂隙水压力存在,在这种情况下的裂纹强度因子,即为式(3.3)中的裂纹强度因子与式(3.18)中的裂纹强度因子的叠加,可表示为

2)法向和切向水压力联合作用下的穿透型裂隙的卸荷损伤的裂纹强度因子(www.xing528.com)

当饱和岩体发生卸荷损伤时,如果岩体中裂隙穿透平面,并且水压力有一个持续的补给,保证裂隙中的水压力处于一个正值。通常岩体裂隙的长度比宽度要大得多,因此,假设在任意点处法向应力均相等,剪应力均相等,岩体裂隙中某点的水压力F可以分解为两个力,一个为法向应力P,另一个则为剪应力Q,对于岩体裂隙内部某点的水压力,如图3.10所示。该处水压力可以表示为

式中:i为比例系数,其值需根据试验测试获取。

根据复变函数中的共形映射原理,可以将图3.10中Z平面上的一条裂纹变为η平面上的一个单位圆,如图3.11所示,经变换、化简,最终则有

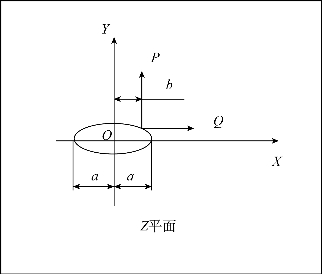
图3.10 Z平面

图3.11 η平面

式中:在平面应力情况下,;对于平面应变情况下,k=1+μ;μ为岩体的泊松比。

对水压力作用下的裂隙局部分析,如图3.12所示,裂隙宽度为3a,利用式(3.21)和式(3.23),根据叠加原理,可得到如下的裂纹强度因子计算公式,即

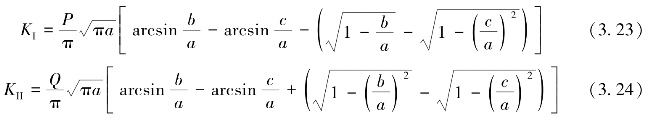
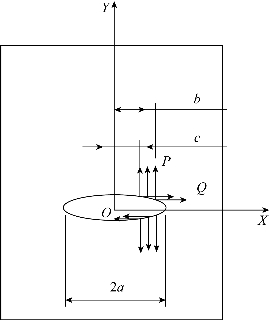
图3.12 局部裂隙水压力分析

对式(3.23)、(3.24)中的c、b两值,分别取c=0、b=a,则可以得到内水压力作用下的半裂隙岩体裂纹强度因子计算公式为

当裂隙中充满水、岩体在进行卸荷时,同时考虑裂隙中法向水压力及水压力的剪切作用时,如图3.13所示,其中图3.13(a)可以分解为图3.13(b)、(c)、(d),而图3.13(b)剪应力不存在,故其裂纹强度因子为

根据叠加原理,可以得到图3.13(a)的裂纹强度因子的计算公式为

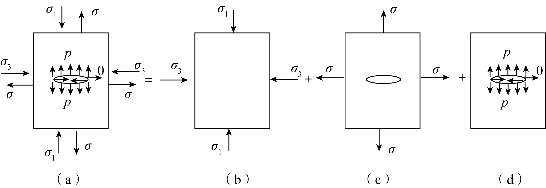
图3.13 裂隙水压力叠加原理

式(3.29)和式(3.30)即为饱和裂隙岩体的卸荷-渗流的损伤裂纹强度因子计算公式。上述公式是在一种理想的情况下所得到的计算公式,而在实际中,由于各种条件的限制,其还仅仅是一种理想化条件下的推导。

3)I型成组穿透型裂隙的卸荷损伤裂纹强度因子

通常,岩体中的裂隙均是成组出现。为了研究实际岩体中裂隙卸荷的损伤情况,在岩体中取一平面,则对岩体卸荷损伤的研究转化为平面问题,假设岩体中的裂隙是长度为2a、间距为2b的裂隙,同时岩体平面比裂隙要大得多,故相对于裂隙来说,可以认为该岩体平面为“无限大”。对于第一种成组出现的裂隙,如图3.14所示,其裂纹强度因子可以采用以下的公式进行计算,即

式中:为单个裂隙的裂纹强度因子的表达式;可看作是由于其他裂隙的存在,对裂纹强度因子的修正。

图3.14 I型成组裂隙

3.岩体卸荷损伤的发展

岩体在卸荷过程中,随着卸荷量的增加,岩体的质量不断地发生劣化,在这一过程中,岩体中的裂隙将产生扩展,使岩体的渗透性增加。

根据断裂力学可知,当岩体裂隙的裂纹强度因子大于临界强度因子时,岩体裂隙将会扩展,对于纯I型与纯Ⅱ型裂隙来说,只要满足以下条件,岩体裂隙将不会扩展,即

对于图3.6所示的I型裂隙,其应力场用极坐标可以表示为

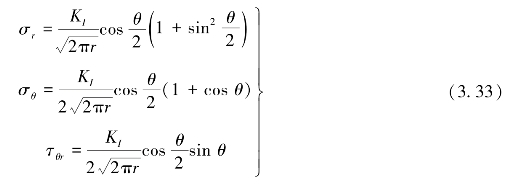
对于图3.7所示的II型裂隙,其应力场用极坐标可以表示为

由于在岩体中,一般两种裂隙同时存在,故对于平面问题,其裂隙尖端的应力场的极坐标可表示为

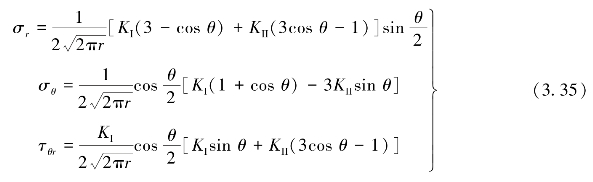
裂隙初始扩展将沿周向法向应力最大的方向发展,因此,当裂隙扩展时,则有

式中:σθ为裂隙扩展角θ处的扩展拉应力。

从而可以得到

对于最大拉应力作用下的裂隙扩展角,取σθ对θ的导数,则有

把式(3.38)和式(3.37)联立可得

式(3.39)求得的θ0就是裂隙的开裂角。

对于纯I型裂隙:

当KII=0,KI≠0时,由式(3.39)可以解得θ0=0或π,θ0=π,对应裂隙闭合;θ0=0,对应裂隙扩展。

这说明对于纯I型裂隙,裂隙将沿原裂隙面发生扩展。

对于纯II型裂隙:

当 时,由式(3.39)可以解得KII(3cos θ0-1)]=0,θ0=±70.5°,即为II型裂隙的开裂角。