裂隙岩体渗流破坏特征分析

1.裂隙岩体渗透系数的确定

对于大多数裂隙岩体来说,基岩与裂隙之间的水流交换比较微弱,水只能沿连通孔隙或裂隙渗透。当岩体内缺陷得到扩展时,这种微弱的水流交换将被放大。假设岩体为多孔的均质材料并且各向同性,那么渗透率可表示为

式中:d为岩体内孔隙的有效直径;c为常数。

当岩体内含有平坦光滑的单个裂隙时,此时裂隙岩体的渗透率可表示为

式中:b为单条裂隙的宽度。

对裂隙岩体介质而言,渗透系数可表示为

式中:ρ为流体密度;η为流体黏度。

由于岩体中孔隙、裂隙等分布的不均匀性和个体间的差异性导致岩体渗流出现非均匀性,即在岩体系统空间内,不同位置上的渗透系数大小不同,此时用渗透张量描述岩体的渗透性,即

渗透张量为对称的二阶张量,其值可表示为

较常用的各向异性岩体渗透张量的表达式为

式中:bh(l)为l组非连续面的等效水力隙宽;λ(l)为l组不连续面之间的距离;n(l)为l组非连续面在法线方向上的余弦。

当岩体内含有裂隙时,此时裂隙岩体的渗透系数可表示为(www.xing528.com)

式中:Kf为裂隙的渗透系数;σ2为垂直于裂隙的应力;σ1、σ3为平行于裂隙的应力;p为裂隙中的裂隙水压力;b0为初始隙宽;kn为法向刚度系数;μ为泊松比;β为裂隙之间接触部分的面积和总面积的比值;η为水流的黏度。

2.渗流-应力耦合作用下裂隙岩体渗透张置演化方程

迄今为止,岩体渗流-应力耦合作用主要表现在岩体的渗透性上,说明岩体的渗透系数是一个与应力有关的函数,渗透系数的确定是研究渗流-应力耦合作用的核心。目前,许多学者建立了多种岩石渗透系数的方程。

1)负指数方程

Louis通过进行钻孔压试验,基于试验结果推出以下公式,即

式中: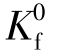为法向应力为0时的渗透系数;σ为法向应力;a为经验系数。

2)负幂指数方程

仵彦卿对某水电工程的岩体进行渗流与应力关系的试验,推导出如下渗透系数计算方法,即

式中:K0为不受应力作用时的渗透系数;σ表示水压作用下的有效应力;c为分数。

该计算公式反映了应力对渗透系数的作用程度,但该方程具有较大的局限性,仅适用于高压应力状况。