层状多孔介质渗透特性优化研究

1.垂直和平行介质层面的流动

构成含水层的多孔介质,渗透性几乎都是不均匀的。然而,当地层由渗透率不同的若干薄层组成时,对于某些简单的流动情形可以计算这种地层的平均渗透率。因为在本节中只考虑均质液体的流动,所以将采用地层的水力传导系数,而不是渗透率。

现考虑均质流体(ρ、η为常数)平行于N个地层流动(见图2.8)。当流动区域的边界上(比如说,点①及点②)存在着与地层相垂直的等势边界条件时,地层中发生的是平行于地层的流动。假设Ki、bi和Qi分别表示第i层的水力传导系数、厚度和单宽流量。如果用Darcy定律写出每一层的流量Qi,则总流量Q应当等于各层流量之和,即

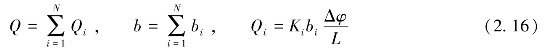
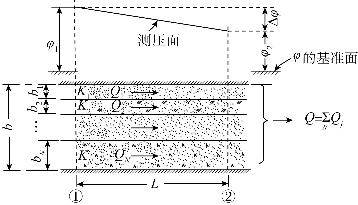
图2.8 承压含水层中平行于层面的流动

但是,梯度J=Δφ/L在各层中保持为常数(即等势面处处与层面垂直)。因此

式中:Ti=Kibi为第i层的导水系数。

如果假定存在一个等效的水力传导系数KP(该系数是与层面平行流动的等效水力传导系数),使得在同样的水力梯度(Δφ/L)作用下,通过相同厚度的含水层(b)传导相同的流量(Q),那么

式中:TP=KPb为含水层的等效导水系数

比较式(2.17)和式(2.18),可以得到

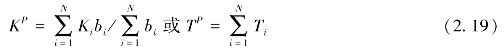
如果用一种水力传导系数沿垂直方向z连续变化[K=K(z)]的地层代替上面的地层,则通过厚度为b,且与层面平行流动的总流量Q应当是

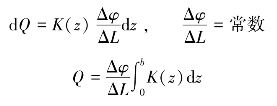
因此

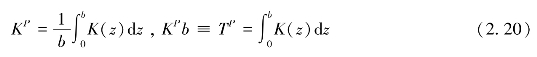
作为第二种简单情况,考虑垂直于层面方向的流动(见图2.9)。因此,流量Q保持不变,而水头的总降落Δφ等于各层水头降落Δφi之和,即

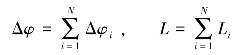
因此

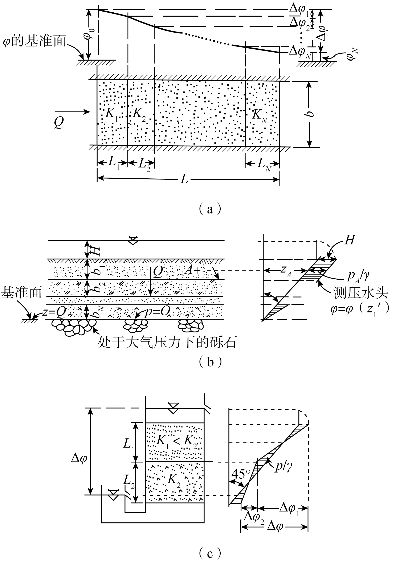
图2.9 垂直于层面方向的流动

(a)承压含水层中垂直于层面的流动;(b)通过层状土的垂直流动,水在大气压力下流出;(c)通过层状土的垂直(饱和)流动,存在一个负压区

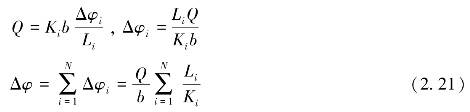
此外,如果假定存在一个等效的水力传导系数KN,使得通过长度为L的地层传导相同的流量Q,那么

因此

应该注意的是,如果有一个Ki=0,即存在一个不透水层,则KN=0,也就是说整个地层系统将变成不透水的。然而,由式(2.22)及下面的式(2.25)能够不用各层的Ki和Li而用各层的阻力或最大一层的阻力来确定流动。

如果用一种水力传导系数水平方向连续变化的地层代替上面的地层系统,则容易证明

假如,将Darcy定律写成如下形式,即

在式(2.24)中,R是长度为L(沿着流动方向)、横截面面积为A的多孔介质块对流体的阻力。于是对于平行于层面的流动,式(2.19)可改写为

而对于垂直层面的流动,式(2.22)可改写为

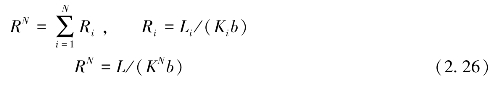
容易看出,式(2.25)和式(2.26)就是计算并联总电阻和串联总电阻的定律。

有时,当流体从一层进入渗透性较大的另一层时,会形成负压区[图2.9(c)]。如果负压不是太高且没有空气进入多孔介质,则流动仍然可以是饱和流动。

由式(2.19)和式(2.22)可以导出KP>KN,也就是说,平行于层面方向的流动的水力传导系数较大,这一点可以证明。

2.任意定向流动的等效水力传导系数

此处是关于流线在水力传导系数不连续平面上折射的讨论。

如图2.10所示,现考察水力传导系数为Ki、厚度为bi(i=0,1,…,n-1,n)的一系列平行均质各向同性地层。在不同水力传导系数的每个界面上,可得方程

Vreedenburgh(1937,也见Maasland 1957)曾提出过一个两层系统的表达式。Marcus和Evenson(1961)按照Vreedenburgh的方法推导了计算n层等效水力传导系数的公式。该公式不要求各层厚度相同(见图2.10)。

(www.xing528.com)

图2.10 层状平行土层中任意方向的流动

由图2.10可以看出

或

并且

在第i层中两条流线之间的流量可以表示为

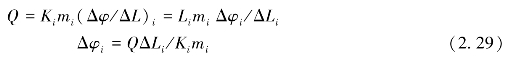
或者根据式(2.27)及式(2.28),得

因此,通过n层水头总损失为

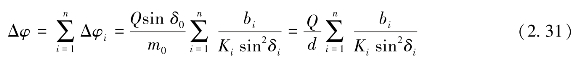
对于等效水力传导系数为Kδ的系统,有

将上两式进行比较,得到

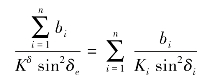
或

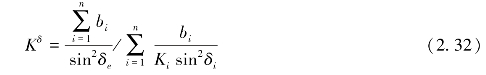
式(2.32)就是所要寻找的等效水力传导系数的表达式。因为1/sin2δe=1+cot2δe,且由其他研究知K0/Kδ=cot δ0/cot δe,故

将式(2.33)代入式(2.32),消去未知角δe,则得

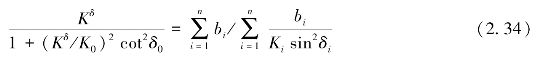
3.作为等效各向异性介质的层状介质

按照Vreedenburgh(1937)和Maasland(1957)对两层系统的研究,Marcus和Evenson(1961)推导了等效水力传导系数Kδ,KN和KP之间的关系式。

由图2.10及式(2.28)可以看出

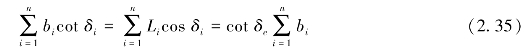
由式(2.27)得

将式(2.35)代入式(2.36)得

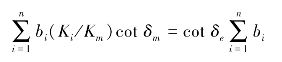
或

改写式(2.32),得

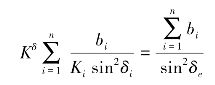
或

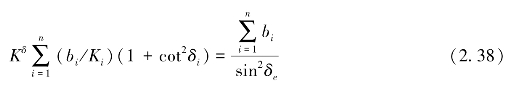
因此,有

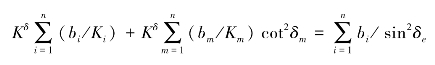
或者利用式(2.37),得

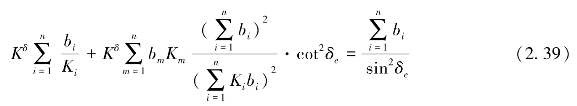
现根据式(2.19)及式(2.22),式(2.39)变为

假如使KP≡Kx,KN≡Ky,则最后这个方程在这里表示沿着角δe所给定的比流量方向的水力传导系数。这说明,层状土的宏观性状即平均性状相当于主水力传导系数为KP和KN的各向异性土壤。但是,为了使这个结论成立,还必须要求各层的厚度较之流动区域的整体尺寸小得多。否则,一点的平均的或等价的水力传导系数的概念就毫无意义。所以,如果考虑图2.10所示的一般情形(及地层的任意组合),则KN和KP在介质的各点不同,因而也就是对于给定方向δe的Kδ在介质的各点上也将变化。此时得到的是一种等效的非均质各向异性介质。当地层以(K1,b1),(K2,b2),(K1,b1),(K2,b2),…的形式交替组合时会出现一种特别有趣的情况。此时我们所得到的介质就其宏观性状而言,应当属于均值各向异性介质(见图2.11)。

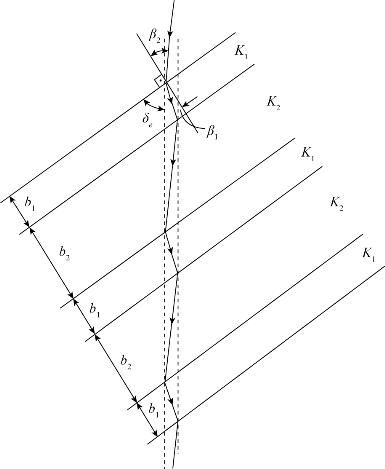
图2.11 以规则方式交替出现的均质各向异性地层系统中任意方向的流动