各向同性介质的水力传导系数优化

1.水力传导系数与渗透率

前面对Darcy定律的概念和表达式进行了介绍。这些表达式中所包含的比例系数K称为水力传导系数,有时,人们也采用渗透系数这个术语。在各向同性介质中,可以将水力传导系数定义为单位水力梯度的比流量。水力传导系数是一个表示多孔介质运输流体能力的标量(量纲为L/T),所以,它与流体及骨架的性质有关。相应的流体性质为密度(ρ)及黏度(η)或它们的组合形式——运动黏度(υ);而相应的骨架性质主要是粒径(或孔径)分布、颗粒(或孔隙)、形状、比表面、弯曲率及孔隙率。从Darcy定律的理论推导或量纲分析可以看出,水力传导系数(Nutting,1930)可表示为

式中:k(量纲为L2)为多孔骨架的渗透率或内在渗透率,它仅与骨架性质有关;γ/η为流体性质的作用。

现有的研究中,有把k与骨架性质联系起来的种种公式。其中,若干公式是纯经验的,如

是根据k(cm2)与平均粒径d(μm)的关系得出的。

另一个例子是从量纲分析导出并为实验所证实的Fair-Hatch(1933)公式,即

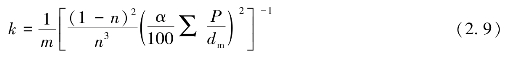
式中:m为排列因素,实验数值约为5;α为砂的形状因素,其值从圆球状颗粒的6.0变化到棱角状颗粒的7.7;P为相邻筛子之间所包含的砂的百分数;dm为相邻筛子额定大小的几何平均值。

除上述经验或实验公式以外,还有从Darcy定律理论推导得出的纯理论公式,在此不再详述,有兴趣的读者可参阅其他文献。

当k在空间上变化,即k=k(x,y,z)时,称多孔介质是非均质介质或非均匀介质。如果在饱和流动区域的某点上k随方向变化,就说介质在该点是各向异性的。由于流体的温度或溶解于流体中的固体的浓度随时间和空间的变化影响着ρ和η,因此也使k在空间和时间上发生变化。

在某些条件下k也可以随时间发生变化。此种变化可以由外部负荷引起,因为外部负荷产生的应力能改变多孔骨架的结构和构造。沉降和固结现象与渗透率的改变有着密切关系。在引起饱和流动的k发生变化的其他因素中,还有固体骨架的溶蚀及黏土的膨胀。在对含有泥质的岩芯测定k的时候,由于岩芯变干会收缩成黏土(尤其是膨润土),所以干燥岩芯对空气的渗透率比用水测定的渗透率大。在岩芯中加入与盐水不同的淡水可以引起黏土膨胀,从而使渗透率变小。

在某些条件下,存在于多孔介质中的生物活动可以逐渐堵塞通道,而使渗透率随时间逐渐减小。在实验室中使用添加剂(如甲醛),能够预防此种堵塞的发生。

2.单位与例子

实践中所使用的水力传导系数K(量纲L/T)的单位是各式各样的。水文工作者喜欢用m/d作单位;而土壤科学家用cm/s作单位。在美国,正像在采用英国单位制的许多国家一样,水文工作者通常使用另外两种单位。一种是实验室水力传导系数单位或称标准水力传导系数单位,利用式(2.3)可以将实验室水力传导系数定义为:在1 ft(1 ft=0.304 8 m)的水力梯度作用下,60 °F的水通过单位面积(ft2,1 ft2=0.092 903 0 m2)的流量(gal(US)/d,1 gal(US)=3.785 41 dm2)。利用这个定义,K的单位为gal(US)(d·ft2)。另一种是野外水力传导系数单位或称含水层水力传导系数单位,按此类方法,仍用式(2.3)将野外水力传导系数定义为:在1 ft/mile(1 mile=1 609.344 m)的水力梯度作用下,野外温度下的水通过厚1 ft、宽1 mile的一个含水层横截面积的流量。这样得到的野外水力传导系数的单位与实验室水力传导系数的单位相同。上述这些单位的换算关系为(www.xing528.com)

在米制单位中,渗透率k(量纲L2)的单位是cm2或m2;在英制单位中,渗透率的单位是ft2。对于20℃的水,有换算关系,即K=1 cm/s相当于k=1.02×10-5 cm2。

采油工程师常用的渗透率单位是d(达西),这个单位是根据公式k=(Q/A)η/(Δp/Δx)得到的,可定义为

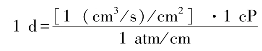
因此,如果完全充满介质空隙空间的、黏度为1 cP(1 cP=10-3 Pa·s)的一种单相流体,在每厘米一个大气压力或与此相当的水力梯度作用下通过横截面积为1 cm2的流量为1 cm3/s,则说这个介质的渗透率为1 d。

1 atm=1.013 2×105 Pa。由达西换算成面积单位的公式为

1 d=9.869 7×10-9 cm2

=1.062×10-11 ft2

=9.613×10-4 cm/s(对于20℃的水而言)

=1.415 6×10-2 gal(US)/(min·ft2)(对于20℃的水而言)

在许多情况下d这个单位太大,因而常用单位是毫达西(10-3 d),记为md。

表2.1(Irmay,1968)列出了水力传导系数和渗透率的一些典型数值。表中是根据美国农垦局的方法用水力传导系数的分级单位表示的。

表2.1 水力传导系数和渗透率的典型数值

K=-log10k