岩体裂隙应力渗流模型优化

20世纪60年代,J.Bellier采用连续介质力学的方法,对完整岩石试件的渗流进行了研究。试件高150 mm,直径60 mm,沿轴向钻一长100 mm、直径12 mm的小孔。实验采用两种方法进行,一种是采用加内水压力来测量渗透系数;另一种为加外水压力来测量渗透系数。由于两种方式对试件的作用不同,使得当内水压力为0.1 MPa时所测得的渗透系数K与外水压力p为5 MPa时所测得的渗透系数之比,可相差100倍,该实验说明岩体中应力状态对渗透系数有很大的影响,如图1.1所示。

图1.1 完整岩石径向加载、卸荷渗流

由于完整岩石试件的渗透系数很小,无法反映岩体中裂隙渗流作用,因此许多学者引用立方定律对单裂隙渗流进行了研究,并用平行板实验进行了验证。20世纪70年代,许多学者直接在岩石试件上形成裂隙研究渗流规律。对于岩体单裂隙渗透系数的实验研究主要采用3种方式:径向流、轴向流和四象限流。Iwai等(1976)采用径向流研究岩体裂隙的渗流;Jones等(1975)采用轴向流方式对岩体裂隙进行了研究。与径向流相比,轴向流的水头分布更加均匀,3种测试方式的示意图如图1.2所示。

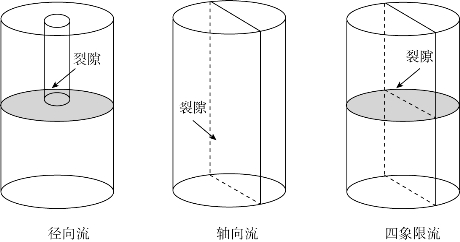
图1.2 3种测试方式示意图

Snow(1965)和Romm(1966)提出了岩体裂隙的渗透张量之后,随着研究的深入和学科的交叉,人们认识到应力与渗透系数相互作用的重要性。Louis(1974)提出了法向应力与渗透系数的关系式,首次探讨了岩体渗流场与应力场的耦合作用机理,之后,岩体应力场与渗流场的研究得到较快的发展。Louis根据某坝址钻孔抽水实验资料分析,得到的裂隙渗透系数(渗透系数)与法向应力σ的经验关系为

式中:为σ=0时的渗透系数;σ=γH-p,γH为研究点的上覆岩层的重量,p为孔隙水压力;a为经验系数,取决于岩石中的裂隙状态。

式(1.1)首次研究了自然状态下非线性破坏岩体中的渗流-应力耦合作用,Louis提出的渗透系数和法向应力呈负指数的关系也被其他的学者所证实。K.Pruess、B.Faybishenko等在野外试验观察的基础上,对水在岩体裂隙中的流动特性进行了探讨,并针对不同的地质条件建立了不同的数学模型,认为水在裂隙中存在着快速优势流动的现象。

Kelsall、P.C.Kesall、J.B.Cass、C.R.Chabannes(1984)研究了地下洞室开挖后渗透系数的变化,导出的法向应力与渗透系数的关系为

式中:Kf为渗透系数;为σ=0时的渗透系数;ξ、A、a为待定系数。

由式(1.2)可知,开挖状态下,渗透系数并非与法向应力呈负指数关系,并且认为导致渗透变化的原因主要有:①应力重新分布,使致密岩石裂隙化;②开挖引起作用于围岩中的天然应力改变,使已有裂隙张开或闭合;③开挖引起的应力释放,导致原生晶面松弛等。

Oda(1986)用裂隙几何张量来统一表达岩体渗流与变形的关系,讨论了等效连续介质模型的应力与应变关系。Erichsen(1987)根据岩体裂隙剪切变形,建立了应力与裂隙渗流之间的耦合关系。

Jakubick、Franz(1993)在对裂隙岩体中开挖隧道后渗透系数变化研究的基础上,认为岩体裂隙渗透系数的增加与裂隙面参数及原始地应力有关。Pyrak-Nolte、Morris(2000)对在力作用下的单裂隙的刚度及流量进行了研究,认为单裂隙刚度与流量之间的关系较为复杂。A.Gudmundsson(2000)研究了流体与单裂隙的长度、宽度之间的关系,认为立方定律适用范围在裂隙长宽比为8～1 000这个范围内。B.Indraratna、G.Ranjith等(2003)为了研究矿井开采引起的瓦斯与水突出的问题,利用三轴仪对高压力下单裂隙的二相流进行研究,认为法向应力对于单裂隙的渗透系数变化起着决定性的作用。

在国内,对于裂隙渗流的研究起步较晚,但也取得了很多创新性的成果。(www.xing528.com)

刘继山(1987、1988)用实验方法研究了单裂隙和两正交裂隙受法向应力作用时的渗流公式;对于单裂隙,渗透系数公式为

式中:uf 0为结构面最大压缩变形量;Kn为结构面当量闭合刚度;H0为压水井中稳定水头;R为影响半径;r0为压水井半径;σ为结构面上的法向应力;γ为水的容重。

郭雪莽(1990)认为,对于层状裂隙岩体,在单轴应力作用下,渗透系数与岩体法向应变之间的关系为

式中:K0为在初始应力σ0下的渗透系数;,e0为初始隙宽,S为裂隙间距,Kn裂隙法向刚度,E为弹性模量;εn为法向应变。

裂隙渗流与应力耦合作用的本质是渗透系数与结构面变形之间的关系,结构面所受的法向应力对于开度的影响将会由渗透系数体现出来。

仵彦卿(1995)通过某水电工程岩体渗流与应力关系实验,得出了岩体裂隙渗透系数与法向应力之间的关系,即

式中:为法向应力σ=0时的渗透系数,D为待定系数,表示裂隙分布的分维数。

窦铁生、陶振宇(1994、1995)对压剪作用下的裂隙岩体的水力学特性进行了初步研究,认为岩体裂隙的开度对其所受的应力极端敏感,岩体的渗透性与岩体的应力有密切的关系;但同时也认为,由于裂隙岩体介质本身的形成过程、几何特性及力学行为的复杂性,还有许多的问题需要进一步的研究。周瑞光等(1996)对金川露天矿F1断层泥和水岩相互作用下的破坏特征进行了研究,采用三轴剪应力仪对断层泥进行了不同含水量的试验,认为断层泥的破坏与含水量、围压及作用时间三者有着密切的联系,并得到了在相同的含水量条件下,随着围压的增加,破坏面与主应力方向夹角逐渐增加的结论。耿克勤等(1996)探讨了岩体裂隙渗透系数与应变、应力的关系,根据岩体裂隙渗流试验结果,采用机械隙宽的概念并根据裂隙岩体的力学本构关系,导出了含一组或多组裂隙岩体的等效渗透系数与复杂应变的耦合关系式。

郑少河等(1999)用三轴仪对单一贯通裂隙岩石试件进行了试验研究,认为天然单裂隙渗透系数与等效法向应力之间存在幂指数关系,为

式中:Kf为天然单裂隙渗透系数;K0为常数;σ1、σ2、σ3为3个法向应力,其中,σ2垂直于裂隙面,σ1、σ3平行于裂隙面;μ为泊松比;p为裂隙水压力;a为系数,取决于裂隙面的粗糙度。

郑少河等认为,在三向应力作用下,垂直于裂隙面的应力对裂隙岩体的渗流特性起主导作用,渗透系数随垂直裂隙面应力的增加而迅速减小。赵阳升(1994、1999)在试验的基础上,提出了块裂岩石的流体力学,对于试验材料采用劈裂试验方式形成岩样渗流裂隙,以模拟张性裂隙性态,该法相当于研究了裂隙与围压垂直时的情况。在试验研究的基础上,赵阳升认为,三维应力场对裂隙渗流有显著的影响,即低应力状态下,渗流较快,表现为显著的裂缝渗流;中应力状态下,表现为孔隙、微裂缝的渗流特征;高应力状态下,即使是裂缝也完全不渗透。

刘才华、陈从新等(2002)对二维应力作用下岩石单裂隙渗流规律进行了试验研究,认为裂隙面的膨胀、收缩及粗糙度的减少均影响岩体的渗流特性,其渗流量的减少主要是由于人造裂隙面的微小变化。

彭苏萍、孟召平(2003)对砂岩在围压下的作用进行了探讨,建立了岩石应力-应变与渗透率之间的定性定量关系,认为渗透率与围压的关系可表示为:k=-aln σ+b,k为渗透率,σ为侧向压力。以上学者对裂隙岩体的水力学特性进行了试验研究,导出了复杂应力状态下的渗透系数与应力、应变的关系。