功能指标分配：如何实现精确管理？

功能指标的分配是指主要结构方案的确定由特征和优化指标共同影响。经过对特征指标的分析，得到了实现特征指标的总体结构初步方案。对于初步方案中具有互补性的环节，还需要进一步统筹分配具体设计指标，要同时考虑特征指标和优化指标进一步确定其具体的实现形式，要根据特征和优化指标的共同影响再进一步确定结构方案。在完成这些工作后，各环节才可采用常规方法进行详细设计。

具有等效性的功能可有多种具体实现形式，在进行功能分配时，应首先把这些形式尽可能地全部列出来。用这些具体实现形式可构成不同的结构方案，其中也包括多种形式的组合方案。采用适当的优化指标对这些方案进行比较，可从中选出最优或较优的方案。优化过程只需计算与优化指标有关的变量，不必等各方案的详细设计完成后再进行。下面以某定量包装秤中滤除从安装基础传来的振动干扰的滤波功能的分配为例，说明等效功能的分配方法。

图8-6是定量包装秤的初步结构方案，其中符号“Δ”表示装置中可建立滤波功能的位置。从安装基础传来的振动干扰经装置基座影响传感器的输出信号，该信号再经放大器、A/D转换器送至控制器，使控制器的控制量计算受到干扰，因而使秤量产生误差。为保证秤量精度，必须采用滤波器来滤除这一干扰的影响。

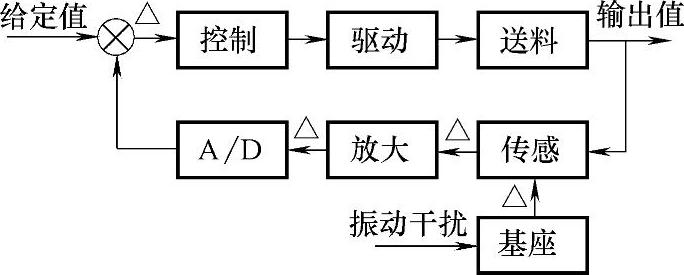
图8-6 定量包装秤初步结构方案

经过分析可知，可以采用三种滤波器来实现这一滤波功能，即安装在基座处的机械滤波器（又称阻尼器）、置于放大环节的模拟滤波器和以软件形式放在控制环节的数字滤波器。这三种滤波器在实现滤波功能这一点上具有等效性，但它们并不是完全等价的，在滤波质量、结构复杂程度、成本等方面它们具有不同的特点和效果。因此，必须根据具体情况从中择优选择一种最合适的方案。

通过对定量包装秤的工作环境和性能要求进行分析，可归纳出选择滤波方案的具体条件为：在存在最低频率为ω₁、振幅为h₁的主要振动干扰的条件下，保证实现以T为工作节拍、精度为K的秤量工作，并且成本要低。因此，可选择成本作为该问题的优化指标，对主要振动干扰的衰减率α₁和闭环回路中所允许的时间滞后T_c特征指标，其中衰减率α₁可根据干扰信号振幅h₁的要求的秤量精度K计算得出，允许的滞后时间T_c可根据工作节拍T和秤量精度K计算得出。详细计算方法这里不再进行讨论。

滤波器放在不同位置，对系统的动态特性会产生不同的影响。由图8-6可以看出，基座形成的干扰通道不在闭环控制回路内，因此，如在这里安装机械滤波器，其衰减率及相位移不会影响闭环控制回路的控制性能，也就是说，不受特征指标的约束，不需要考虑相位特性，因而衰减率可以设计得足够大，容易满足特征指标α₁要求。但是由于干扰信号的最低频率ω₁值较小，机械式滤波器的结构较复杂，体积较大，因而成本也较高。

模拟式滤波器可以与放大器设计在一起，也可单独置于放大环节之后，但不论放在哪一位置，都是在闭环回路内。由于ω₁干扰信号的频率较低，所以这里应采用低通滤波器。由低通滤波器的特性可知，当在控制回路内串入低通滤波器后，将使控制系统的阶跃响应时间增加，相位滞后增大，快速响应性能降低。因此，模拟滤波器性能的选择受特征指标T_c的约束，不能采用高阶低通滤波器，而低阶低通滤波器的滤波效果又较差。

数字波滤器的算法种类较多，本例采用算术平均值法来实现低通滤波。同模拟滤波器一样，由于数字滤波器需要计算时间，因此也受允许的滞后时间T_c的限制，且对较低频率的干扰信号，抑制能力较弱，但数字滤波器容易实现，且成本较低。

通过上述分析可见，三种滤波器各有特点，因此需要采用优化方法合理分配滤波功能，以得到最优方案。为了讨论问题方便，这里只选成本作为优化指标，将特征指标作为约束条件，构成单目标优化问题。由于方案优化是离散形式的，故采用列表法较为方便、直观。具体作法是：首先根据滤波器的设计计算方法，求出各种实现形式在满足约束条件下的一定范围内的有关性能指标，将这些性能指标列成表格，按表选择可行方案，然后再对各可行方案进行比较，根据优化指标选择出最优方案。(www.xing528.com)

表8-4 滤波器特性

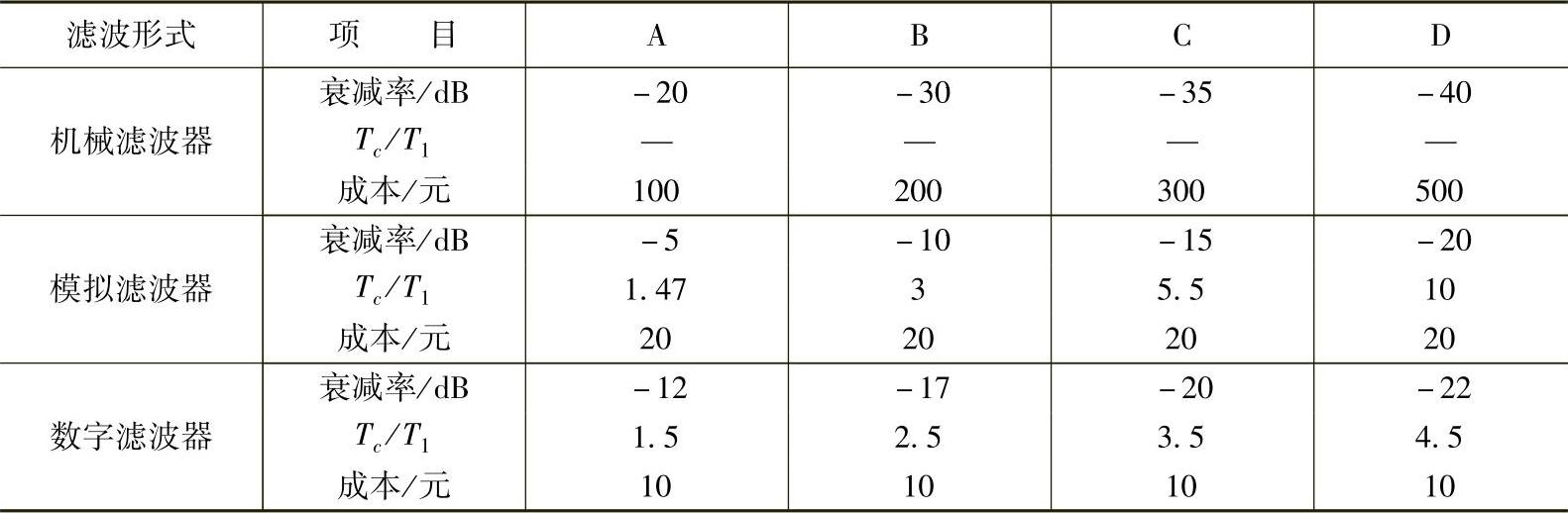
表8-4列出了上述三种滤波器的特征指标和优化指标值，其中A、B、C、D是四个不同的品质等级；T_c/T₁是允许的滞后时间与频率为ω₁的干扰信号周期之比。由于机械滤波器所在位置不影响系统动态特性，故表中相应位置没有列出这项指标。

由表8-4可见，当干扰信号周期T₁大于允许的滞后时间T_c时，即T_c/T₁＜1时，模拟滤波器和数字滤波器都不能满足系统动态特性的要求，这时只能选择机械滤波器。

现假设约束条件为T_c/T₁≤5.5，α₁≤-40dB。由表8-2可知，单个模拟滤波器和单个数字滤波器都无法满足该约束条件，因此必须将滤波器组合起来（即由几个滤波器共同实现滤波功能）才能构成可行方案。

从表8-4中选出满足约束条件的可行方案列于表8-5，其中总特征指标值为构成可行方案的各滤波器的相应特征指标值之和。依据成本这一优化指标，可从表8-5所列出的四种可行方案中选出最合理的方案，即方案3。该方案采用机械滤波器和数字滤波器分别实现对干扰信号的衰减，衰减率均为-20dB，也就是说，将滤波功能平均分配给机械滤波器和数字滤波器，同时还满足另一约束条件T_c/T₁=3.5＜5.5，而且该方案成本最低。

应当指出，表8-5中并未将所有可行方案列出，因此，方案3并不一定是所有可行方案中的最优方案；此外，当约束条件改变时，将会得到不同的可行方案组及相应的最优方案。

表8-5 满足条件的可行滤波方案