电路网络包括无源电路网络和有源电路网络两部分。建立电路网络动态模型依据的是电路方面的物理定律,如基尔霍夫定律等。使用复阻抗的概念通常使电路建模较为方便,这时电阻值用R表示,电感值用Ls表示,而电容值用1/Cs表示,这样可以用s的代数方程代替复杂的微分方程。从而方便地得到电路网络系统的传递函数。
同时,我们引入动态结构图的概念。
(1)RC网络
对于如图5-19所示的RC网络,可以用消元的方法求出它的传递函数。但我们知道,如果方程组的子方程数较多,消元法比较麻烦,而且消元之后,仅剩下输入和输出两个变量,信号中间的传递过程得不到反映。采用动态结构图,能形象直观地表明输入信号在系统或元件中的传递过程。因此,也可把动态结构图作为一种数学模型,并在控制系统中得到了广泛的应用。另外,由动态结构图求传递函数,显得更简单方便。
1)RC有源网络
由图5-19可知,RC网络的微分方程组为:
ui=Ri+uo
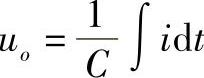
或写成
ui-uo=Ri
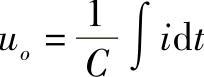
对上面二式进行拉普拉斯变换,得:
Ui(s)-Uo(s)=RI(s) (5-24)

将式(5-24)写成
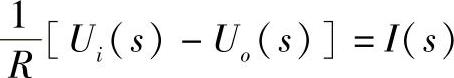
这一数学关系可用图5-20形象表现出来。同样,式(5-25)可用图5-21表示。
将图5-20和图5-21合并,网络的输入量置于图的左端,输出量置于图的右端,并将同一变量的信号通路连在一起,即得到RC网络的动态结构图,如图5-22所示。由图可以写出RC网络的传递函数:

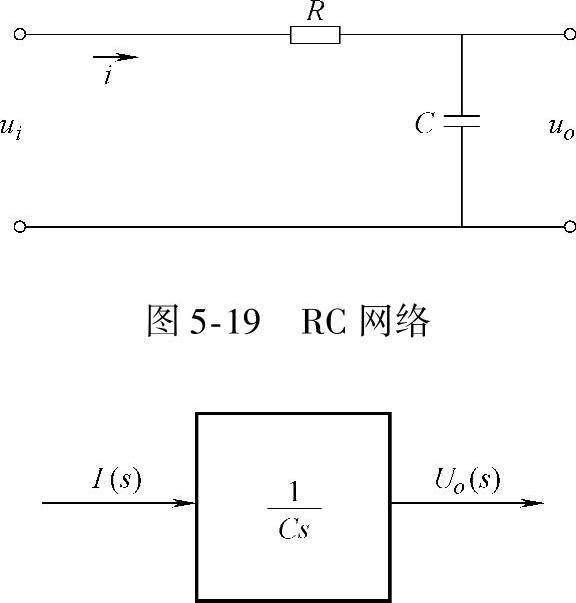
图5-21 式(5-25)图形
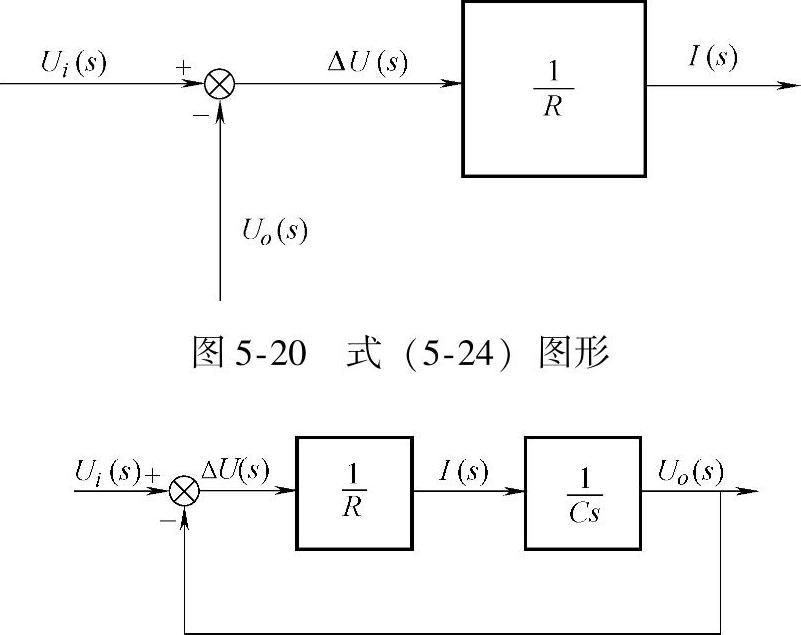
图5-22 RC网络动态结构图
2)RC无源网络
如图5-23a所示的RC无源网络,利用复阻抗的概念可直接写出以下关系式:
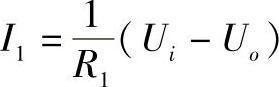
I2=Cs(Ui-Uo)
I=I1+I2
Uo=I·R2
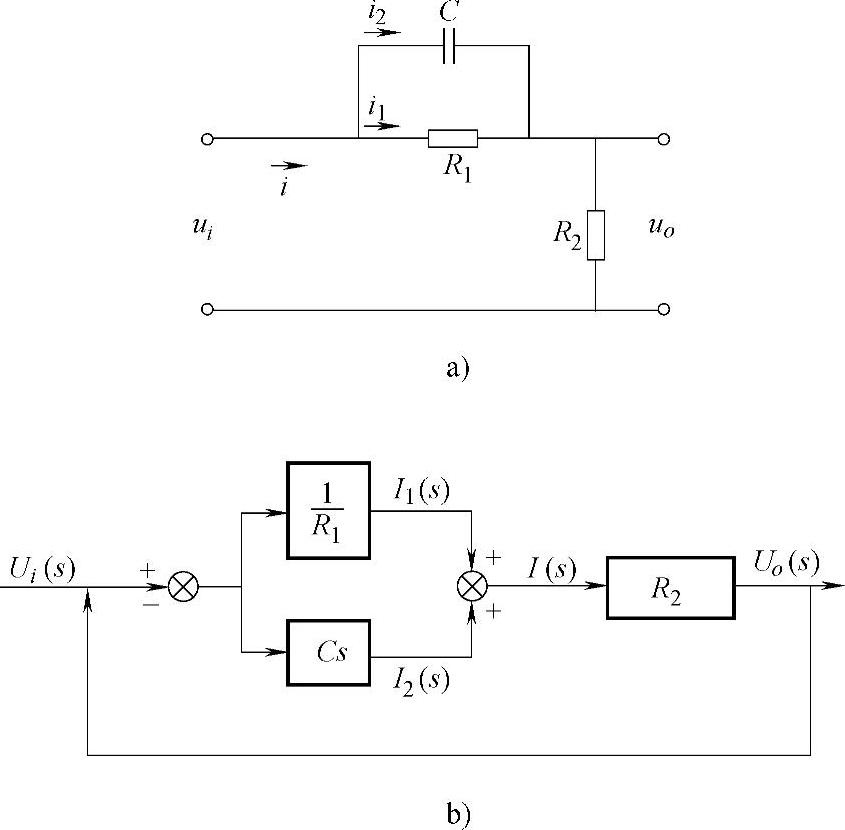
图5-23 RC无源网络及其动态结构图
a)RC无源网络 b)动态结构图
由以上关系式可建立动态结构图如图5-23b所示。由图可得出系统传递函数为:
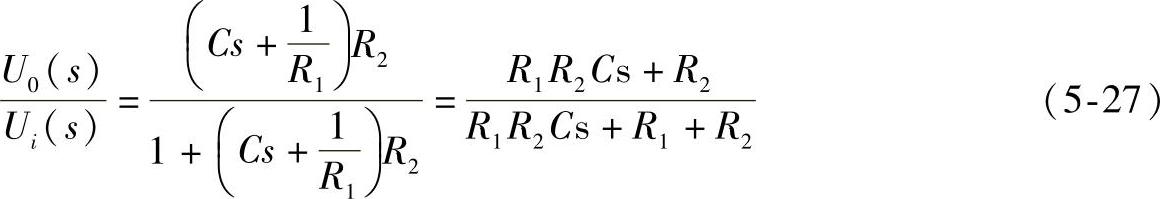
对于只要求传递函数的无源网络,不必画出其动态结构图。由于无源电路网络内部不含任何电压源或电流源,只由电阻、电容、电感组合而成,因此对于串联网络,复阻抗等于各串联复阻抗之和;对于并联网络,复阻抗的倒数等于各并联复阻抗的倒数之和。通过这样的简化,利用复阻抗分压,往往就可以求出多数无源网络的传递函数。
(2)无源双T网络
如图5-24所示电路为无源双T网络。由图可得到下列方程组:

由上述方程组消去中间变量Ua(s)和Ub(s),求得传递函数为:

进一步,令s=jω,可得该网络频率特性为:
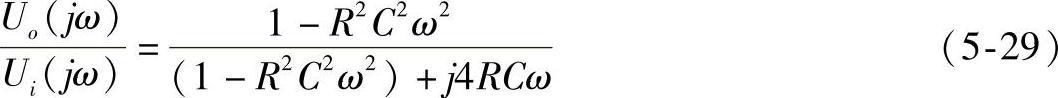
由上式可见,当频率很低或很高时,该网络放大倍数接近1,当ω=1/RC时,放大倍数为零。因此选择合适的电阻R和电容C的值,就可以滤掉频率为ω的干扰,这是一种使用效果很好的带阻滤波器。(https://www.xing528.com)
(3)运算放大器
运算放大器等有源器件,由于其开环放大倍数大、输入阻抗高、价格低,获得了越来越广泛的应用。由运算放大器组成的有源网络,在很多场合可取代无源网络。运算放大器相互连接时,由于各运算放大器的输入阻抗很高,可以忽略负载效应。系统数学模型可通过分别求取各运算放大器的数学模型得到,大大简化了建模的步骤,降低了难度。各个运算放大器的模型一般可通过反馈复阻抗对输入复阻抗之比求得。
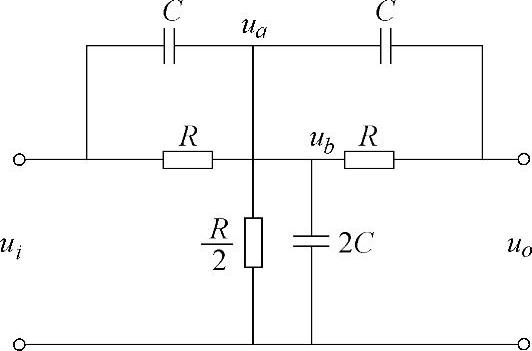
图5-24 无源双T网络
图5-25为运算放大器工作原理图。由于运算放大器的开环增益极大,输入阻抗也极大,所以把A点看成“虚地”,即UA≈0,同时i2≈0及i1≈-if。
于是有:
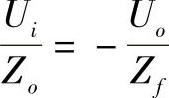
对上式进行拉普拉斯变换,有:
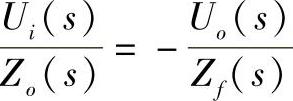
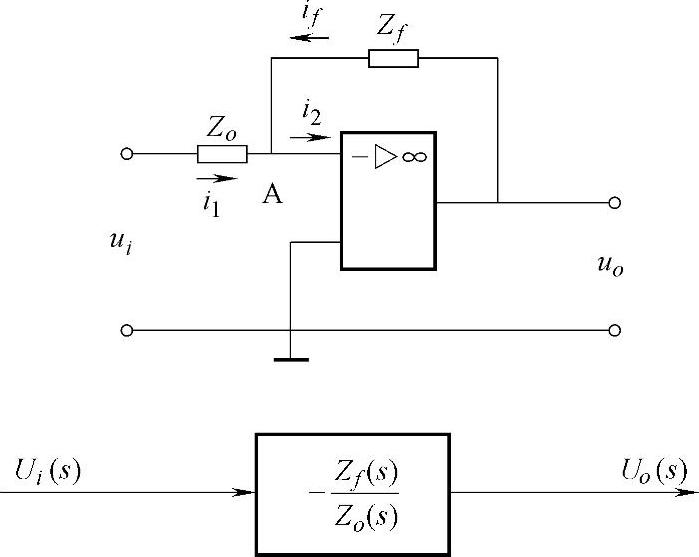
图5-25 运算放大器工作原理图
因此,运算放大器的传递函数为:

式中,Zf(s)和Zo(s)代表复阻抗。
由式(5-30)可见,若选择不同的输入电路阻抗Zo和反馈回路阻抗Zf,就可组成各种不同的传递函数,这是运放的一个突出优点。应用这一点,可以做成各种调节器和各种模拟电路。
(4)比例-积分调节器
图5-26为比例-积分(PI)调节器的结构图,由图可求出传递函数为:
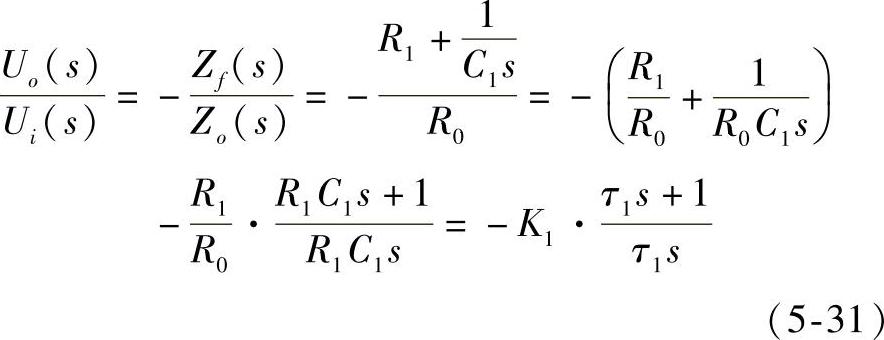
式中,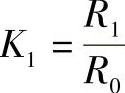 ;τ1=R1C1。
;τ1=R1C1。
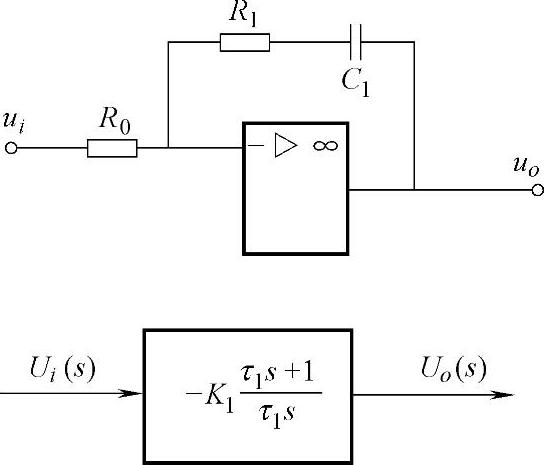
图5-26 比例-积分调节器结构图
(5)比例-微分调节器
图5-27为比例-微分(PD)调节器的结构图,由图可求出其传递函数为:
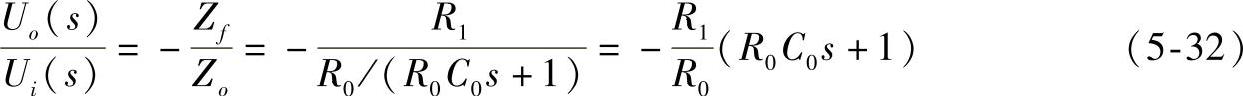
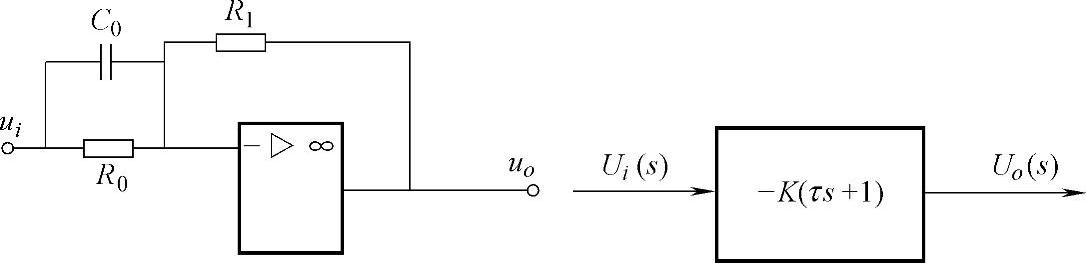
图5-27 比例-微分调节器结构图
(6)有源带通滤波器
如图5-28所示是一种有源带通滤波器。如图所示,设中间变量i1(t)、i2(t)、i3(t)、i4(t)和ua(t),按复抗阻,可写出如下代数方程组:
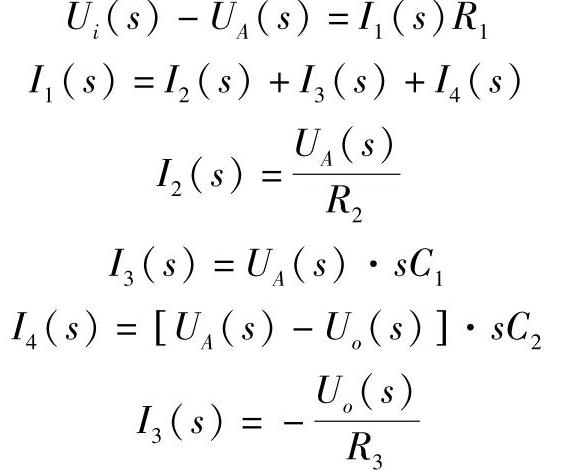
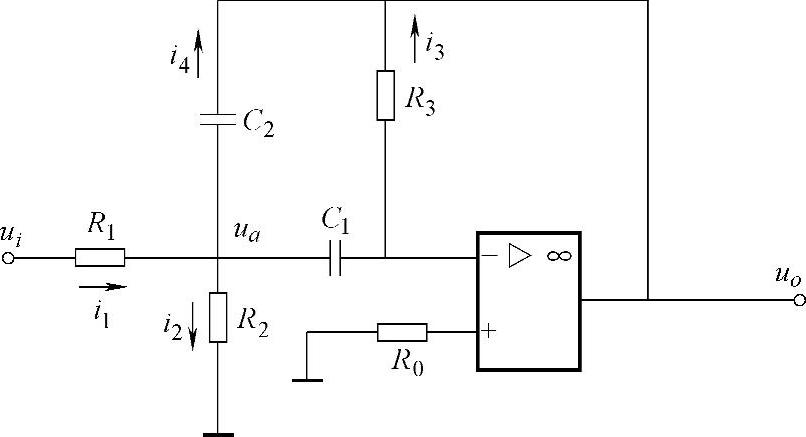
图5-28 有源带通滤波器
消去中间变量,I1(s)、I2(s)、I3(s)、I4(s)和UA(s),得该网络传递函数为:
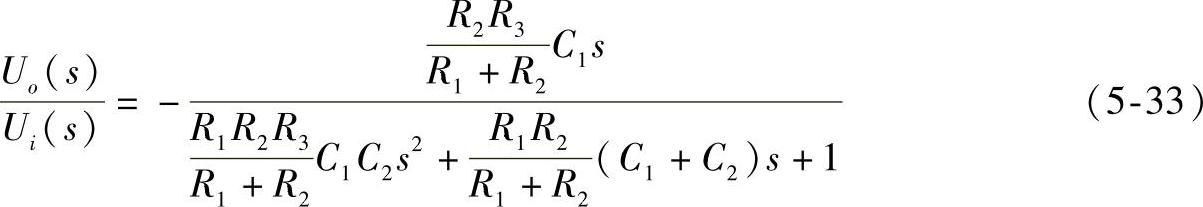
图5-29是一种滤除固定频率干扰的有源带通滤波器。如图所示,设中间变量ua(t)和ub(t),则有如下代数方程组:
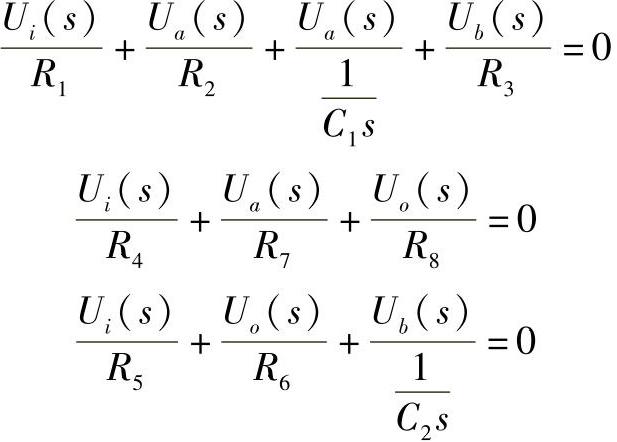
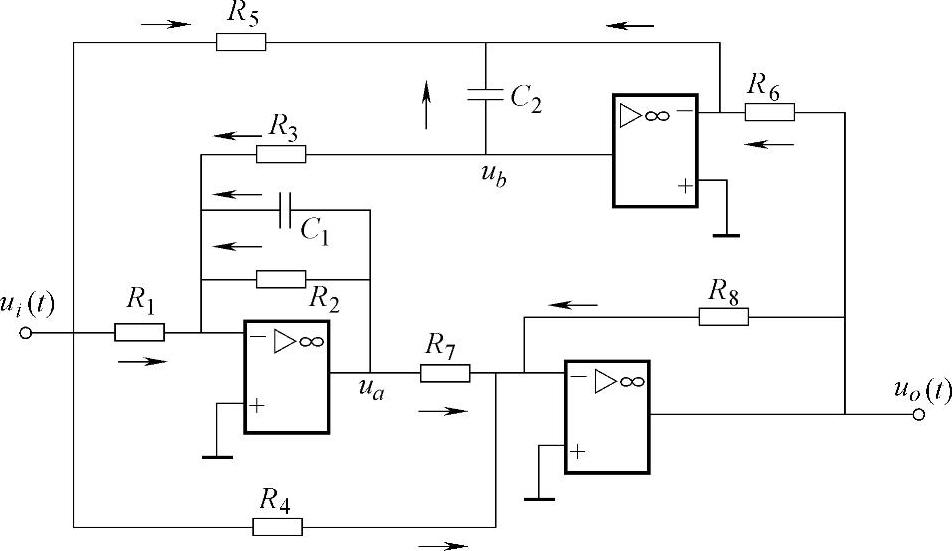
图5-29 滤除固定频率干扰的有源带通滤波器
消去中间变量Ua(s)和Ub(s),可得系统传递函数为:
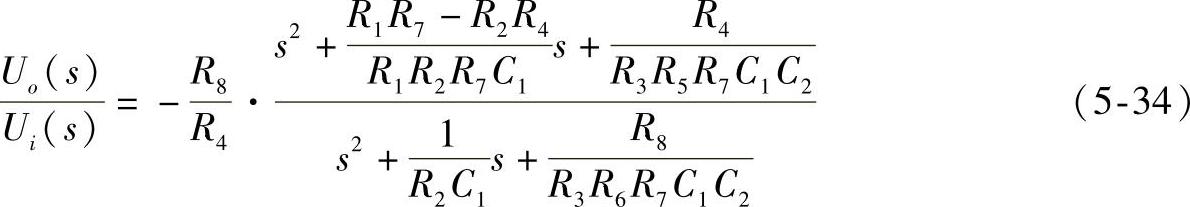
选R1R7=R2R4,R4/R5=R8/R6,则上式变为
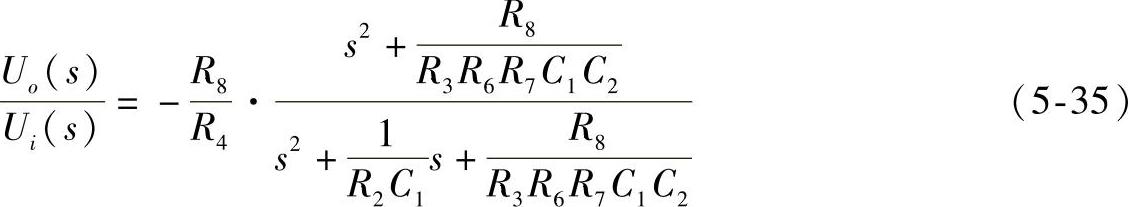
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




