【摘要】:机械转动系统的基本元件是转动惯量、阻尼器和弹簧。由图可得到转动惯量的数学模型为:图5-15 机械转动系统基本元件a)转动惯量 b)阻尼 c)弹簧黏滞阻尼器的数学模型为:弹簧的数学模型为:M=K[θ1-θ2] 下面举例说明机械转动系统的建模方法。图中,J表示摆锤的转动惯量;f表示摆锤与空气的黏性阻尼系数;K表示扭簧弹性刚度。
机械转动系统的基本元件是转动惯量、阻尼器和弹簧。如图5-15所示是三个元件的表示符号,图中,M(t)代表外力矩;θ(t)代表转角;J代表转动惯量;f代表黏滞阻尼系数;K代表弹簧刚度。由图可得到转动惯量的数学模型为:

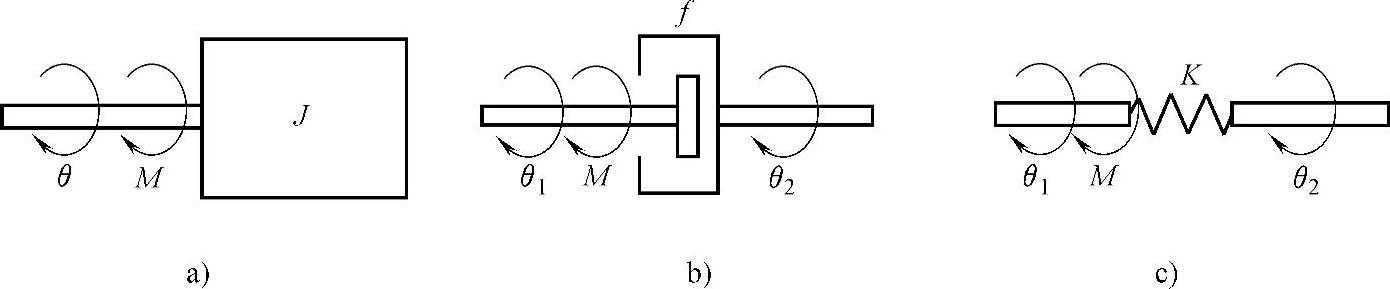
图5-15 机械转动系统基本元件
a)转动惯量 b)阻尼 c)弹簧
黏滞阻尼器的数学模型为:
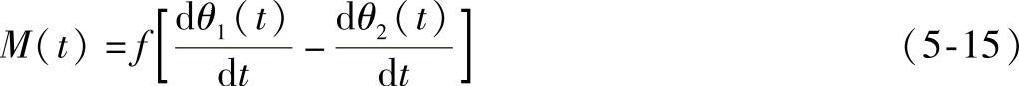
弹簧的数学模型为:
M(t)=K[θ1(t)-θ2(t)] (5-16)
下面举例说明机械转动系统的建模方法。
图5-16为一个扭摆的工作原理图。图中,J表示摆锤的转动惯量;f表示摆锤与空气的黏性阻尼系数;K表示扭簧弹性刚度。则加在摆锤上的力矩M(t)与摆锤转角θ(t)之间的运动方程为:
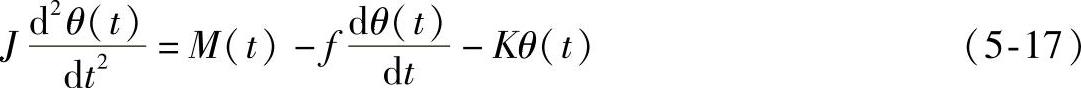
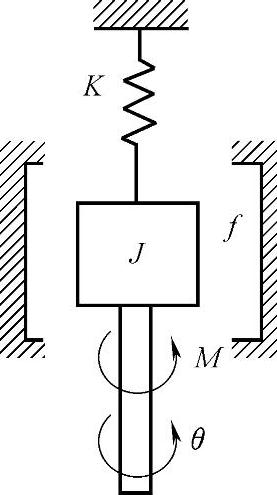
图5-16 扭摆工作原理图
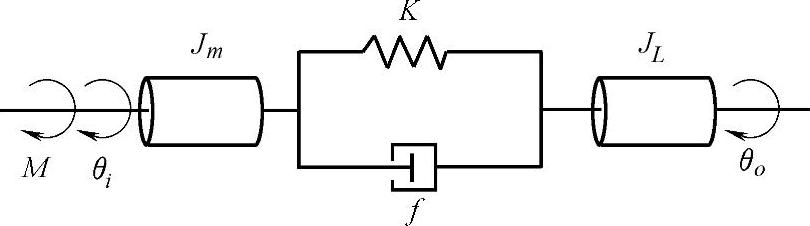
图5-17 同步齿形带驱动装置示意图(https://www.xing528.com)
对上式取拉普拉斯变换,得该系统传统函数为:

图5-17为打印机步进电动机同步齿形带驱动装置示意图。图中K,f分别表示同步齿形带的弹性与阻尼;M(t)为步进电动机的力矩;Jm和JL分别为步进电动机轴和负载的转动惯量;θi(t)与θo(t)分别为输入轴与输出轴的转角。
针对输入轴和输出轴可以分别写出力矩平衡方程:
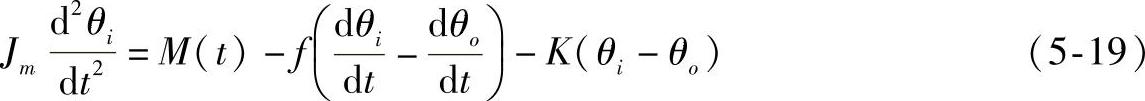
及
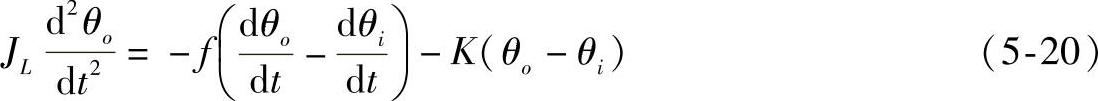
对上两式取拉普拉斯变换得:
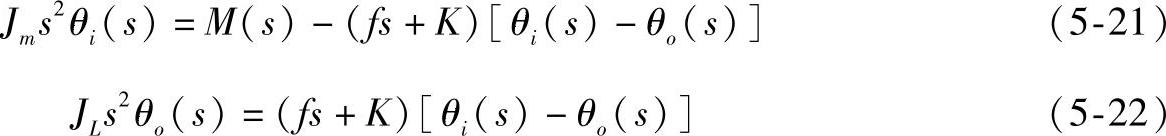
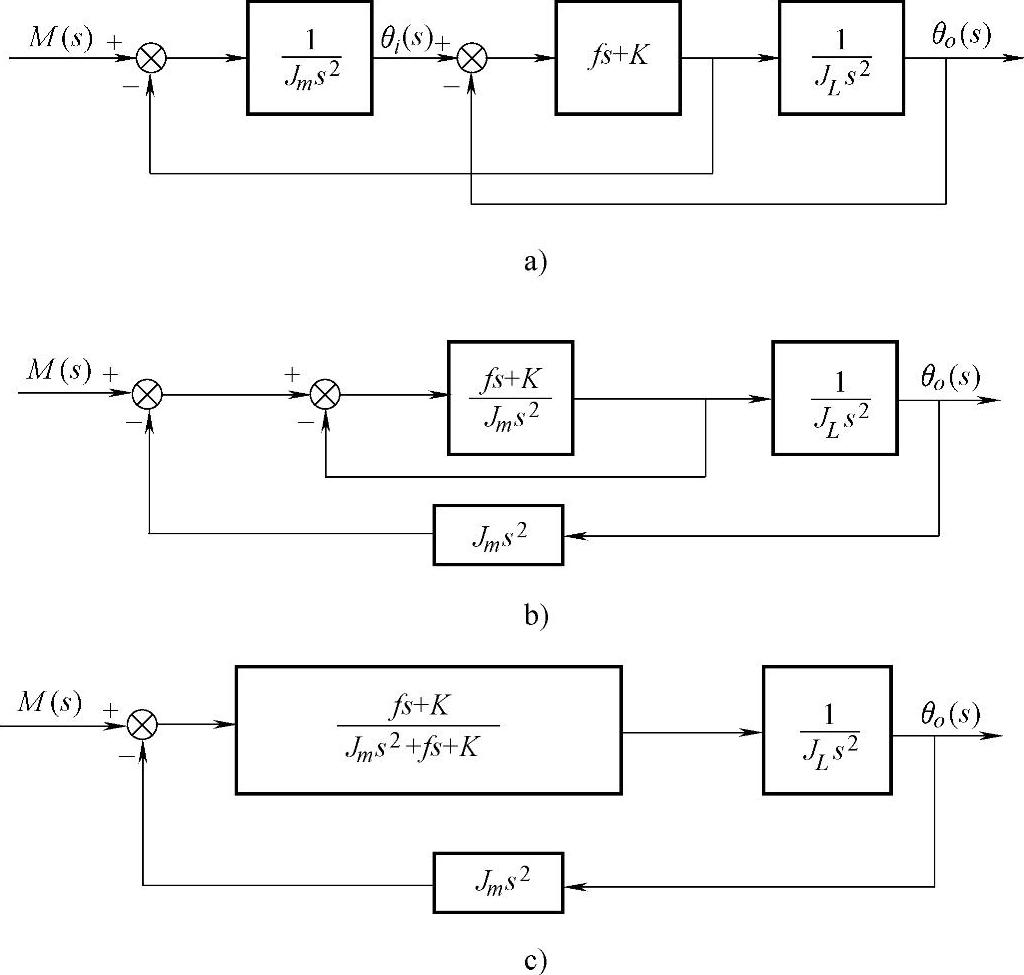
图5-18 同步齿形带系统方框图
a)系统方框图 b)方框图化简 c)化简后的方框图
根据式(5-21)和式(5-22)可画出系统方框图如图5-18a所示,并依次简化为图5-18b和图5-18c。由图5-18c可得该系统的传递函数为:
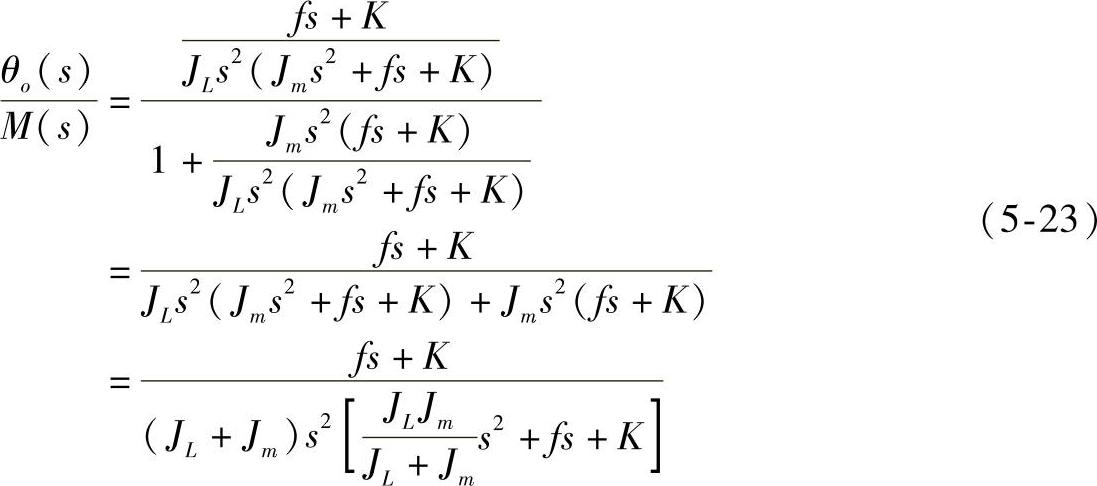
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




