插值法及分段方法应用详解

插值法是当前最为常用的非线性误差补偿方法，它结合了计算法和查表法的优点，即首先利用查表法确定数据所处分段，然后在分段内采用相对简单的数学表达式来拟合数据曲线，改善了查表法带来的表格编制的困难，减少了列表点和测量次数。

（1）插值原理

假设输出电信号与被测参数之间的函数表达式为y=f（x），该公式不是简单的线性方程。插值法先将该函数按一定的要求分成若干段，然后在相邻的分段点之间利用直线代替曲线，即可求出输入值x所对应的输出值y。对于任一x在（x_i，x_i+1）之间，则对应的被测参数值为

将上式简化，有：y=y_i+k_i(x-x_i) （4-30）

y=y_i0+k_ix （4-31）

式中 y_i0=y_i-k_ix_i，。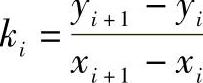

（2）插值算法

根据上文提到的插值原理，接下来介绍一下计算机程序的插值算法：(www.xing528.com)

1）首先，用试验的方法测出传感器的变化曲线y=f（x），为了避免人为操作等带来的误差，需要重复测量，选择测量数据较为稳定的输入输出曲线。

2）将试验曲线分段，分段方法主要有等距分段法和非等距分段法两种。等距分段法即沿x轴等距离选取插值基点，这种方法中x_i+1和x_i是常数，计算十分简单，但对于曲率或斜率变化明显的曲线，等距分段法会产生较大误差，而要想减小误差，则必须把基点分得很细，这样又占用很大内存，效率较低。非等距分段法通常主动的将常用刻度范围插值距离划分的小一些，而非常用的刻度区域插值距离划分的大一些，该方法插值点的选取较为复杂。

3）确定插值点的坐标值（x_i，y_i），以及相邻插值点之间的斜率k_i。

4）对于任意的x值，计算x-x_i，并根据该值找出区域（x_i，x_i+1）和该段斜率k_i。

5）根据（x_i，x_i+1）和k_i，以及公式计算y值。

除了上述非线性处理方法，还有许多其他的方法，例如最小二乘法、函数逼近法、数值积分法等，具体选择何种方法进行非线性处理，需要根据实际情况来确定。