滤波器的幅频特性及其带宽与测量响应的矛盾问题

传感器信号的传输过程中可能包含大量的噪声，因此，信号的处理主要是指对信号的滤波处理，这一过程一般是通过滤波器来完成的。滤波器是一种选频装置，可以使信号中特定的频率成分通过，而极大衰减其他频率成分。利用滤波器的这种筛选作用，可以滤除干扰噪声。滤波器在自动检测、自动控制及电子测试仪器中被广泛使用。

根据滤波器所处理的信号性质，分为模拟滤波器与数字滤波器。下面分别进行介绍。

（1）模拟滤波

模拟滤波器主要对模拟信号进行滤波。根据滤波器的选频作用，一般将滤波器分为四类，即低通、高通、带通和带阻滤波器。图4-31所示为这四种滤波器的幅频特性。

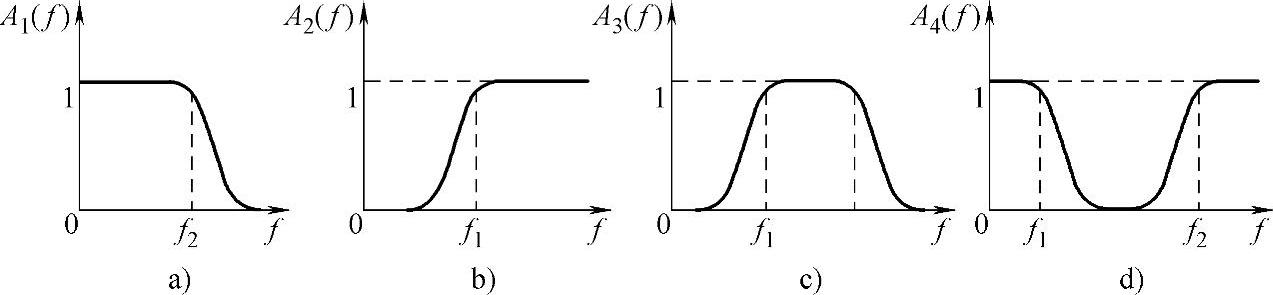
图4-31 四类滤波器的幅频特性

a）低通 b）高通 c）带通 d）带阻

根据滤波器的幅频特性示意图可知，滤波器可以分为通频带、阻频带和过渡带三个大致区域。通频带能够使相对应的频率成分几乎不受衰减地通过，阻频带则几乎完全阻碍相应的频率成分通过，在通带与阻带之间存在的一个过渡带，其幅频特性是一条斜线，在此频带内，信号受到不同程度地衰减。这个过渡带只能尽量减小，而不可避免。

①低通滤波器

通频带频率从0～f₂，幅频特性平直。低通滤波器可以使信号中低于f₂的频率成分几乎不受衰减地通过，而高于f₂的频率成分受到极大地衰减。

②高通滤波器

与低通滤波器相反，从频率f₁～∞为其通频带，其幅频特性平直。它使信号中高于f₁的频率成分几乎不受衰减地通过，而低于f₁的频率成分将受到极大地衰减。

③带通滤波器

它的通频带在f₁～f₂之间。它使信号中高于f₁并低于f₂的频率成分几乎不受衰减地通过，而其他成分受到极大地衰减。

④带阻滤波器

与带通滤波器相反，其阻带在频率f₁～f₂之间。它使信号中高于f₁并低于f₂的频率成分受到极大地衰减，其余频率成分几乎不受衰减地通过。

如图4-31所示的是四种滤波器的幅频特性曲线在通带与阻带之间都有一段倾斜的过渡曲线，使通带与阻带不能截然分开。在人们的想象中，过渡曲线若是一条陡峭的垂线才好，以低通滤波器为例，人们希望低通滤波器可以将输入信号中频率小于f₂的各成分所构成的信号无失真地筛选出来，而将频率大于f₂的各成分完全衰减掉。然而，理想滤波器在物理上是不可能实现的。理想滤波器的意义仅在于供理论研究之用，以及用以建立评价滤波器的指标。

以理想滤波器为基础，则有式（4-24）成立：

BT_e=常数 （4-24）

即低通滤波器对阶跃响应的反应时间T_e和带宽B成反比，或者说带宽和反应时间的乘积为常数，这一结论对其他滤波器（高通、带通、带阻）也适用。(www.xing528.com)

滤波器带宽代表其频率分辨力，它随着通带的变宽而降低。因此，式（4-24）表明，滤波器的高分辨能力和测量时快速响应的要求是互相矛盾的。滤波的带宽增加必然导致测量速度下降，甚至会产生谬误和假象。但对已定带宽的滤波器，过长的测量时间也是不必要的。一般采用BT_e=5～10已足够了。

（2）数字滤波

数字滤波是通过一定的计算或判断提高信号的信噪比。数字滤波可以采用软件来实现，在机电一体化系统中应用十分广泛。下面介绍几种常用的数字滤波方法。

1）算术平均值法

算术平均值法是寻找一个S值，使该值与各采样值间误差的平方和为最小，即：

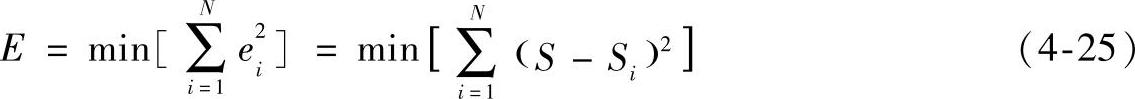
为使平方和E最小，对式（4-25）进行求导，可得算术平均值法的算式：

式中 S_i为第i次采样值，S为信号滤波后的输出，N为采样次数。其中，N的选择应按具体情况决定。N越大，平滑度越高，灵敏度越低，但是计算量越大。对于不同的类型的信号，可以取不同的N值，例如，流量信号可以取N=12，压力信号可以取N=4。

2）中值滤波法

中值滤波法是通过连续检测三个采样信号，从中选择居中的数据作为有效信号。采用这种方法可以滤除三个采样信号中的一次干扰信号，当三个采样信号中包含两次异向干扰信号时，也能保证正确选择有效信号。但是，对于两次干扰信号为同向信号，或者三个采样信号同为干扰信号的情况，中值滤波法则无能为力。中值滤波法能够滤除脉冲干扰，常用于缓慢变化过程的滤波，不适用于快速变化过程的滤波。

3）防脉冲干扰平均值法

该方法结合了算术平均值法和中值滤波法，该方法的原理是先运用中值滤波法滤除脉冲干扰，然后对剩下的采样信号进行算术平均。

若S₁≤S₂≤…≤S_N，则

S=(S₁+S₂+…+S_N)/(N-2) （4-27）

式中，一般取3≤N≤14，当N等于3时，式（4-27）等同于中值滤波法。

防脉冲干扰平均值法综合了算术平均值法和中值滤波法的优点，具有较好的滤波质量。

除了以上三种基本的数字滤波方法之外，还有惯性滤波、程序判断滤波等许多类型的滤波方法，可以查阅相应的著作进一步深入了解和研究。