时序逻辑电路及其状态方程与状态表分析

组合逻辑电路的输出只与当时的输入有关，而与电路以前的状态无关。时序逻辑电路则是一种与时序有关的逻辑电路，它以组合电路为基础，又与组合电路不同。时序逻辑电路的特点是在任何时刻电路产生的稳定输出信号不仅与该时刻电路的输入信号有关，而且还与电路过去的状态有关。时序逻辑电路是由组合电路和存储电路两部分组成。

时序电路可以分为同步时序电路和异步时序电路两大类。在同步时序电路中，电路的状态仅仅在统一的时钟信号控制下同时变化，如果没有时钟信号，即使输入信号发生变化，电路的输出可能会被影响，但电路的状态不会被改变；在异步时序电路中，存储电路的状态变化不是同时发生的，这种电路中没有统一的时钟信号，任何输入信号的变化都可能立刻引起异步时序电路状态的变化。

此外，有时还根据输出信号的特点将时序电路划分为米利（Mealy）型和穆尔（Moore）型两种。其中米利型电路的输出信号不仅取决于存储电路的状态，而且还取决于输入变量，即该电路的输出是输入变量和现态的函数。而在穆尔型电路中，输出信号仅仅取决于存储电路的状态。可见，穆尔型电路只不过是米利型电路的一种特例而已。

鉴于时序电路在工作时是在电路的有限个状态之间按一定规律转换的，因此在有些文献中又将时序电路称为有限状态机（Finite State Machine）或算法状态机（Algorithmic State Machine）。它是一个从实际中抽象出来的数学模型，用来描述一个系统的操作特性。

由于时序逻辑电路与组合逻辑电路在结构和性能上存在不同，因此在研究方法上两者也有所不同。组合电路的分析和设计主要用到的工具是真值表，而时序电路的分析和设计主要用到的工具是状态转换表（简称状态表）和状态图。

时序电路中用“状态”来描述时序问题。使用“状态”概念后，我们就可以将输入和输出中的时间变量去掉，直接用表达式来说明时序逻辑电路的功能。所以“状态”是时序电路中非常重要的概念。

我们把正在讨论的状态称为“现态”，用符号Q表示；把在时钟脉冲CP作用下将要发生的状态称为“次态”，用符号Q^∗表示。描述次态的方程称为状态方程，一个时序电路的主要特征是由状态方程给出的，因此，状态方程在时序逻辑电路的分析与设计中十分重要。

用于描述时序电路状态转换全部过程的工具主要有状态表和状态图。它们不但能说明输出与输入之间的关系，同时还表明了状态的转换规律。这两种方法相辅相成，经常配合使用。

在时序电路中用表格方式表示的状态转换关系，称为状态表。具体做法是将任意一组输入变量及存储电路的初始状态取值，代入状态方程和输出方程表达式进行计算，可以求出存储电路的下一状态（次态）和输出值；把得到的次态又作为新的初态，和这时的输入变量取值一起，再代入状态方程和输出方程进行计算，又得到存储电路新的次态和输出值。如此继续下去，将全部的计算结果列成真值表的形式，就得到了状态表。

例3-7 用状态表来表示图3-46所示米利型时序电路。

解：该电路的输入为x，输出为y=xQ₂，设触发器Q₂和Q₁的初始状态为Q₂Q₁=00。若x=0，则当第一个CP脉冲到来时，由于T₁=1，触发器Q₁翻转为1，而T₂=0，触发器Q₂保持0不变，即Q₂Q₁转换为01，输出y=0；同理，第二个CP脉冲到来时，Q₂Q₁转换为10，y=0；第三个脉冲到来时，Q₂Q₁转换为11，y=0。依次类推，当x=0时，Q₂Q₁的状态转换规律为00→01→10→11→00→…，输出y总为0。

同理可以分析出，当x=1时，Q₂Q₁的状态转换规律为00→11→10→01→00→…，输出y相应为1→0→0→1→1→…。

该电路内部状态有四个：00，01，10和11，分别用状态q₀，q₁，q₂和q₃来表示。由此列出状态表如表3-9所示。

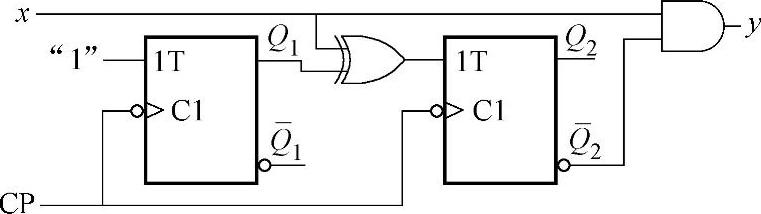
图3-46 例3-7的米利型时序电路

表3-9 例3-7的状态表

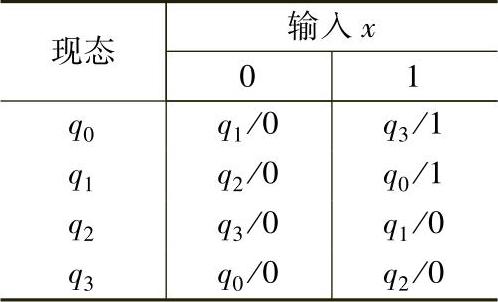
表格上方从左到右列出输入的全部组合，表格左边从上到下列出电路的全部状态作为现态，表格的中间列出对应不同输入和现态下的次态和输出。如表格中间部分的第二行第一列的单元格表示，处于状态q₁（Q₂Q₁=01）的时序电路，当输入x=0时，输出y=0，在时钟脉冲CP的作用下，电路进入次态q₂（Q₂Q₁=10）。(www.xing528.com)

例3-8 用状态表来表示图3-47所示穆尔型时序电路。

解：该电路的工作情况与图3-45相同。输出y=Q₂Q₁，它与电路的输入x无关，而只与电路的状态有关，因此这是一个穆尔型时序电路。当输入x=0时，Q₂Q₁的状态转换规律为00→01→10→11→00→…，相应的输出y为0→0→0→1→0→…；当输入x=1时，Q₂Q₁的状态转换为00→11→10→01→00→…，相应的输出y为0→1→0→0→0→…。同样，该电路内部状态有四个：00，01，10和11，分别用状态q₀，q₁，q₂和q₃来表示。

由此列出状态表，如表3-10所示。

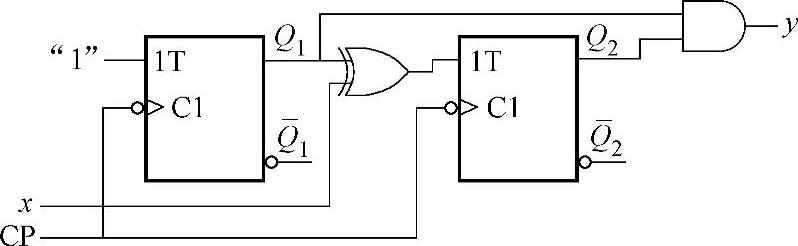
图3-47 例3-8的穆尔型时序电路

表3-10 例3-8的状态表

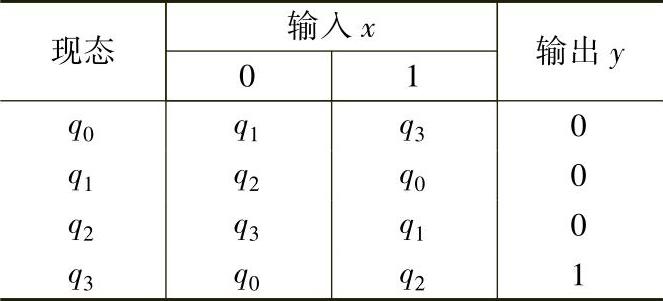
由于穆尔型时序电路的输出y仅与电路的状态有关，所以将输出单独作为一列，其值完全由现态确定。以表3-10中第二行（现态为q₁的行）为例说明时序电路状态表的读法：当电路处于状态q₁（Q₂Q₁=01）时，输出y=0。若输入x=0，在时钟脉冲CP的作用下，电路进入次态q₂（Q₂Q₁=10）；若输入x=1，则在时钟脉冲CP的作用下，电路进入次态q₀（Q₂Q₁=00）。

在时序逻辑电路中用图形方式表示的状态转换关系，称为状态图（或状态转换图）。米利型时序电路的状态图如图3-48所示。在状态图中，每一个状态q_i用一个圆圈表示，用带箭头的直线或弧线表示状态的转换方向，并把引起这一转换的输入条件和相应的输出条件标注在有向线段的旁边（x/y）。例如，可将图3-46所示电路的状态表描述为图3-49所示的状态图。

穆尔型时序电路的状态图中，输出y与状态q写在一起，表示y只与状态有关，即在圆圈内标以q/y；输入仍标在有向线段的旁边。上例图3-47电路的状态图如图3-50所示。

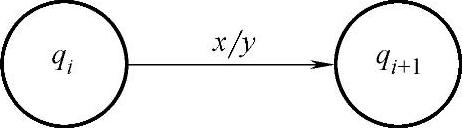
图3-48 米利型时序电路状态图

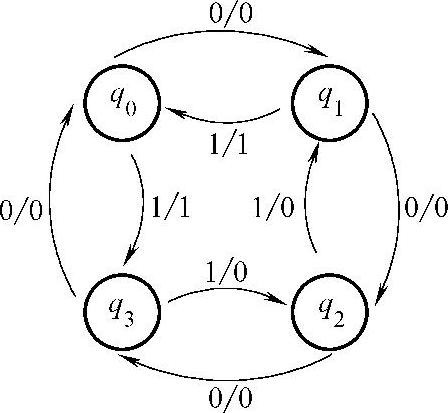
图3-49 例3-7电路的状态图

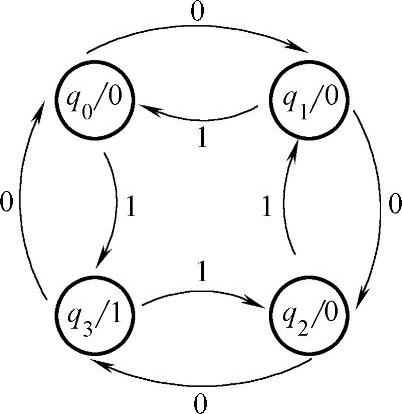
图3-50 例3-8电路的状态图