信号处理中的滤波器设计与应用

（1）滤波电路

在电子技术和控制系统领域中，广泛使用着滤波电路。它的作用是让负载需要的某一频段的信号顺利通过电路，而其他频段的信号被滤波电路滤除，即过滤掉负载不需要的信号。

对于幅频特性，通常把能够通过的信号频率范围定义为通带，而把受阻或衰减的信号频率范围称为阻带，通带与阻带的界限频率称为截止频率。按照通带与阻带的相互位置不同，滤波电路通常可分为四类，即低通滤波（LPF）电路、高通滤波（HPF）电路、带阻滤波（BEF）电路和带通滤波（BPF）电路。四类滤波电路的幅频特性如图3-17所示，其中实线为理想特性，虚线为实际特性。各种滤波电路的实际幅频特性与理想情况是有差别的，设计者的任务是力求向理想特性逼近。

1）无源滤波电路

无源滤波电路是由无源元件（电阻、电容及电感）组成。由于此类滤波电路不用加电源，因而称为无源滤波电路。图3-18所示的是无源低通滤波电路和无源高通滤波电路。

对于图3-18a和3-18b所示电路，滤波的截止频率均为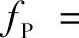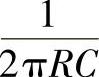。当信号频率等于截止频率时，也就是电容的容抗等于电阻阻值时，有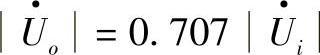。对于频率f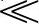f_P的信号，有容抗X_C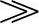R，信号能从图3-18a电路通过，但不能从图3-18b电路通过；对于频率f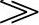f_P的信号，有容抗X_C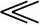R，信号不能从图3-18a电路通过，但能从图3-18b电路通过。幅频特性如图3-19所示。

图3-17 四类滤波电路的幅频特性

a）低通滤波 b）高通滤波 c）带阻滤波 d）带通滤波

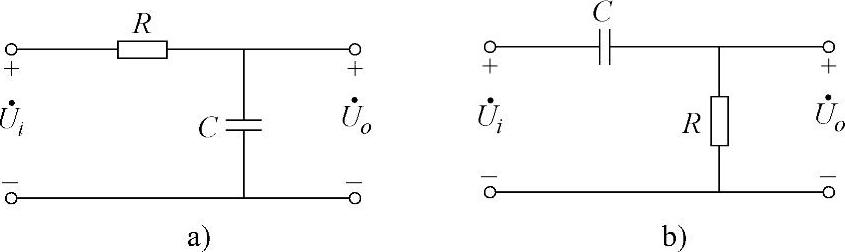
图3-18 无源滤波电路

a）低通滤波 b）高通滤波

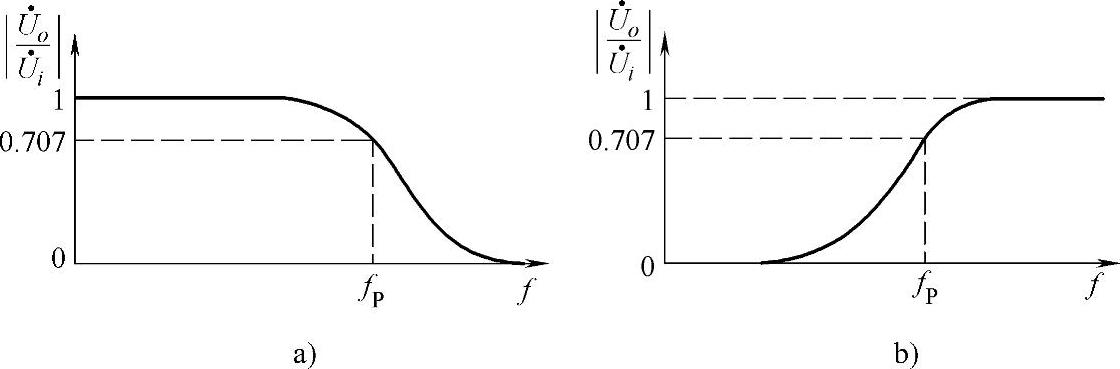
图3-19 无源滤波幅频特性

a）低通滤波 b）高通滤波

无源滤波电路的优点是结构简单，无需外加电源。但有以下缺点：R和C上有信号电压降，故要消耗信号能量；带负载能力差，当在输出端接入负载R_L时，滤波特性随之改变；滤波性能也不大理想，通带与阻带之间存在着一个频率较宽的过渡区。

图3-20 有源滤波电路的构成

2）有源滤波电路

如果在无源滤波电路之后，加上一个放大环节，则构成一个有源滤波电路，如图3-20所示。有源滤波电路的放大环节可由分立元件电路组成，也可以由集成运算放大器组成。若引入电压串联负反馈，以提高输入电阻、降低输出电阻，则可克服无源滤波带负载能力差的缺点。若适当地将正反馈引入滤波电路，则可以提高截止频率附近的电压放大倍数，以补偿由于滤波阶次上升给滤波截止频率附近的输出信号所带来的过多衰减。由此可见，有源滤波将大大提高滤波性能。

①有源低通滤波

a.一阶电路：电路如图3-21a所示，它由一节RC低通滤波电路及同相比例放大电路组成。它不仅使低频信号通过，还能使通过的信号得到放大。

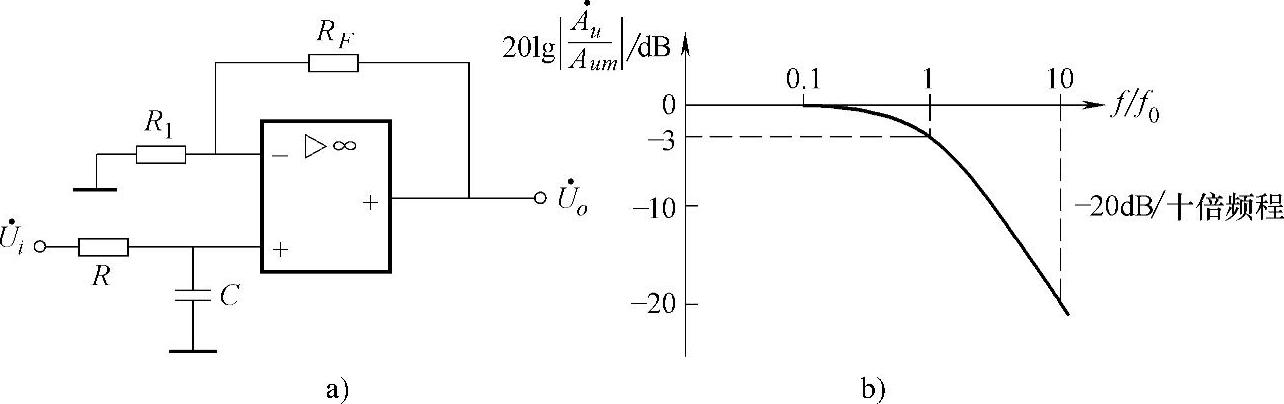
图3-21 同相输入一阶有源低通滤波电路及幅频特性曲线

a）电路 b）幅频特性

根据虚断特性，有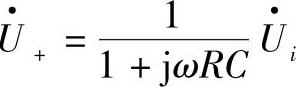。根据虚短特性，又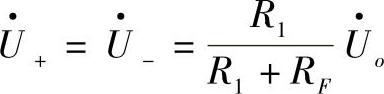有。因此有：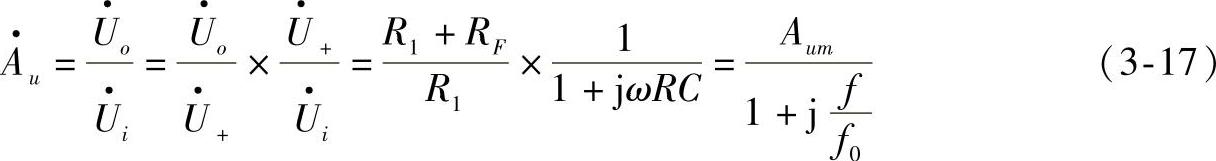

式（3-17）中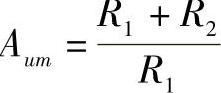，，为通带电压放大倍数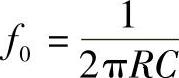；，为特征频率。由于式（3-17）中分母f的最高次幂为一次，故称为一阶滤波器，其幅频特性表达式为：

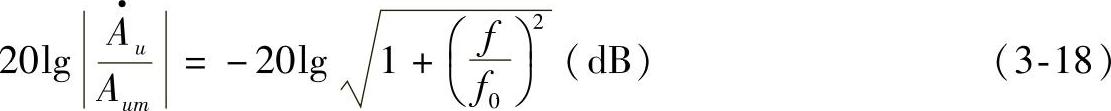
幅频特性曲线如图3-21b所示。当f=f₀时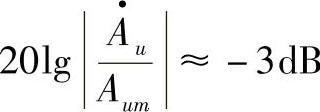，，所以通带的截止频率f_P=f₀。当f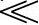f_P时，。当ff_P时，特性曲线按-20dB/十倍频程的速率下降。

一阶低通滤波的滤波特性与其理想特性相比，差距很大。在理想情况下，希望当f＞f_P后，电压放大倍数立即下降到零，使大于截止频率的信号完全不能通过低通滤波器。但是，一阶低通滤波的对数幅频特性只是以每十倍频程-20dB的速率缓慢下降。为了使滤波特性接近于理想情况，可采用二阶低通滤波电路。

b.简单的二阶电路：如图3-22a所示，它由两节RC低通滤波电路及同相比例放大电路组成。经推导，电压放大倍数表达式为：

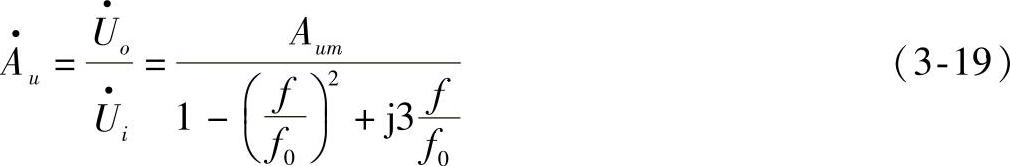(www.xing528.com)

式（3-19）中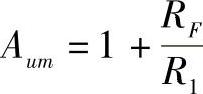，，为通带电压放大倍数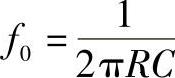；，为特征频率。由于式3-19分母中f的最高次幂为二次，故称为二阶滤波器。若令式（3-19）分母的模等于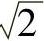，则可求出低通的截止频率为：

f_P≈0.37f₀ （3-20）

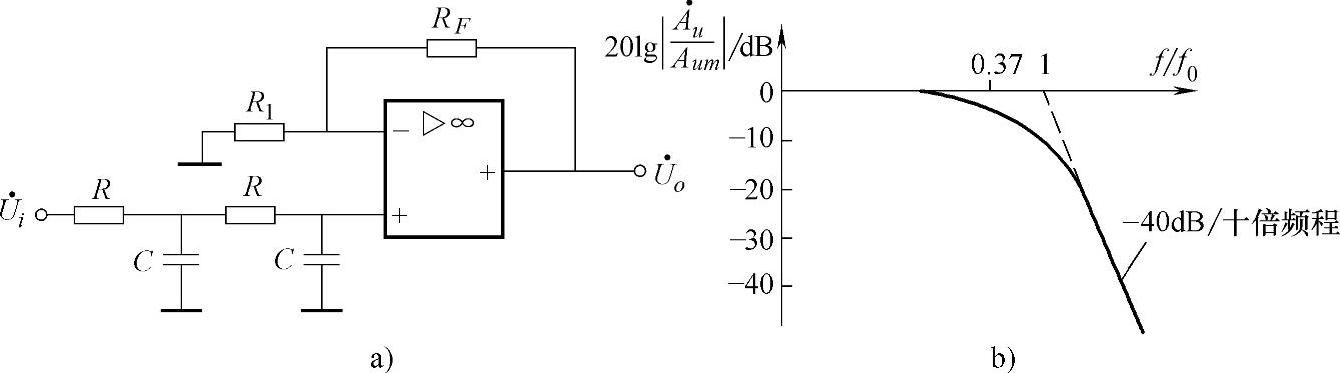
图3-22 简单二阶有源低通滤波电路及幅频特性曲线

a）电路 b）幅频特性

幅频特性如图3-22b所示。虽然衰减斜率达-40dB/十倍频程，但是f_P远离f₀。若使f=f₀附近的电压放大倍数数值更大，则可使f_P接近于f₀，滤波特性趋于理想。

c.压控电压源二阶电路：电路及幅频特性如图3-23所示，因同相端电位控制由运算放大器和R_F及R₁组成的电压源来完成，故称为压控电压源二阶低通滤波电路。与图3-22所示电路不同的是，滤波电容C₁由原来接地改接到集成运算放大器的输出端，从而引入正反馈。若C₁=C₂=C，则滤波的特征频率。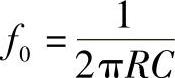

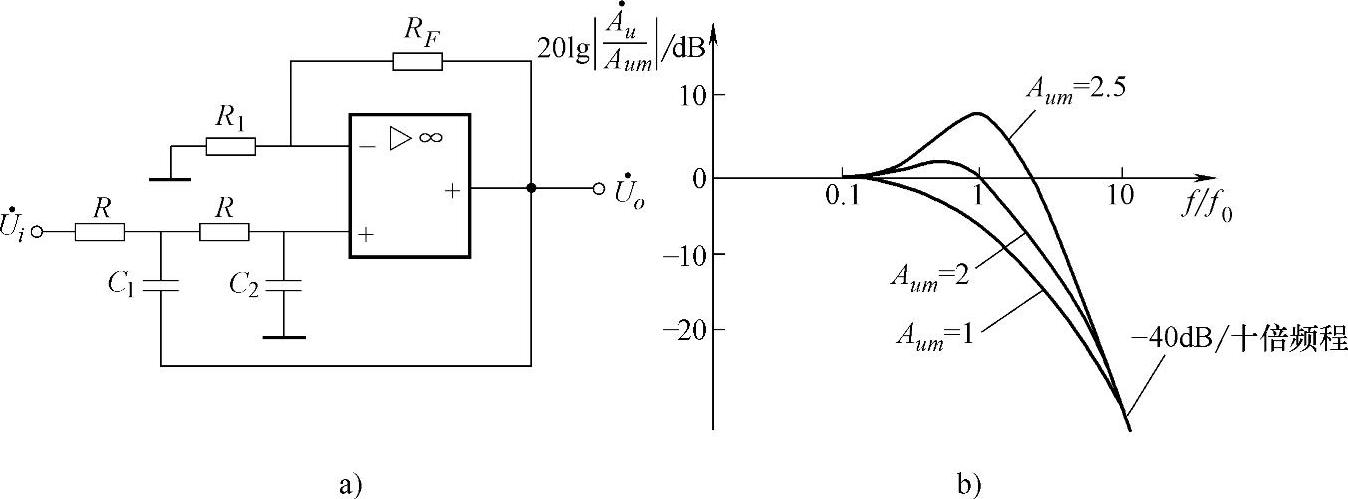
图3-23 压控电压源二阶低通滤波电路及幅频特性曲线

a）电路 b）幅频特性

当f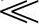f₀时，由于C₁容抗趋于无穷大，正反馈很弱；又C₂容抗趋于无穷大，输入信号没有被衰减；此时通带电压放大倍数为A_um=1+R_F/R₁。当f=f₀时，每级RC低通移相为-45°，两级RC低通移相为-90°。因此，当f接近于f₀时，由C₁引回来的反馈基本上是正反馈，从而使f₀频率附近的放大倍数增大，并随着A_um的增大而出现峰值，如图3-23b所示。

当ff₀时，由于C₂容抗趋于零，输入信号被衰减到零；而且C₁和C₂各自移相近似为-90°，则总移相趋于-180°，于是C₁引回来的反馈成为负反馈，使放大倍数按-40dB/十倍频程速率下降。

经推导，电压放大倍数可写成

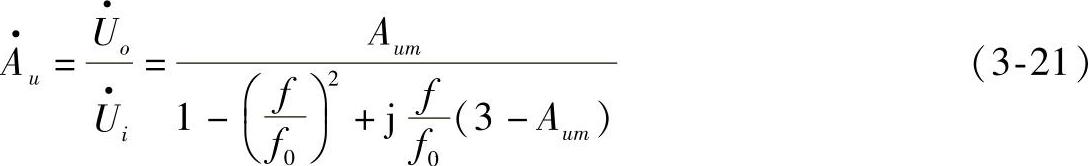
式（3-21）表明，电路应避免A_um=3的情况，否则电路将产生自激振荡。

②有源高通滤波

高通滤波电路与低通滤波电路具有对偶性，如果将图3-21和图3-22所示电路中的滤波环节的电容换成电阻，电阻换成电容，则可分别得到同相输入一阶3-24a、同相简单二阶3-24b电路。

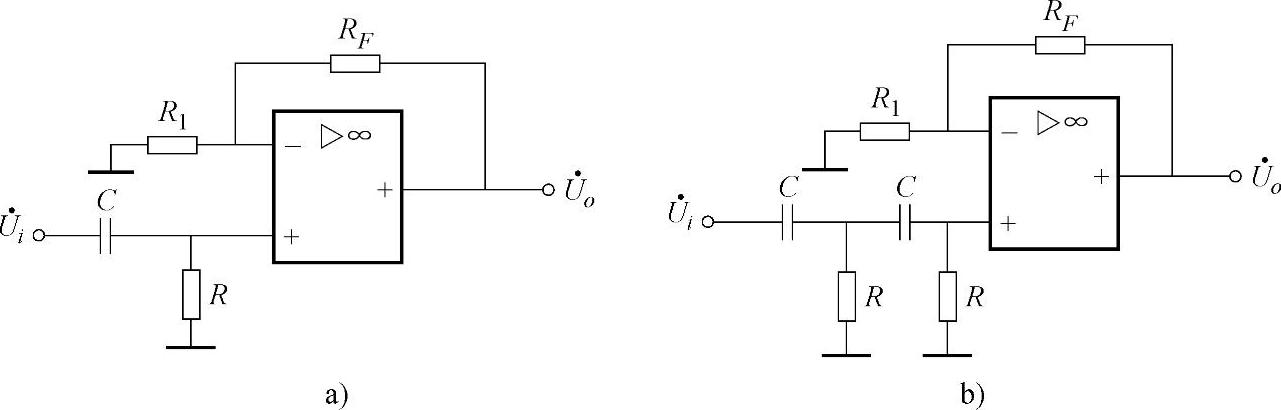
图3-24 有源高通滤波电路

a）同相一阶 b）同相简单二阶

③有源带通滤波

带通滤波电路仅让某一频段的信号通过，而让该频段以外的所有信号被阻断。实现带通滤波的方法很多，将低通滤波电路与高通滤波电路串联，就可以得到带通滤波电路，如图3-25所示。要求低通滤波的截止频率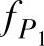应大于高通滤波的截止频率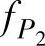，通带为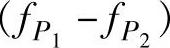。将带通滤波电路与放大环节结合，就得到有源带通滤波电路。

④有源带阻滤波

带阻滤波电路又称陷波电路，与带通滤波电路相反，带阻滤波电路阻止或衰减某一频段的信号，而让该频段以外的所有信号通过。实现带阻滤波的方法很多，将输入信号同时作用在低通滤波电路和高通滤波电路上，再将两个电路的输出信号相加，就可以得到有源带阻滤波电路，如图3-26所示。要求低通滤波的截止频率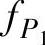小于高通滤波的截止频率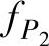，则阻带为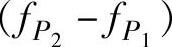。将带阻滤波电路与放大环节结合，就得到有源带阻滤波电路。

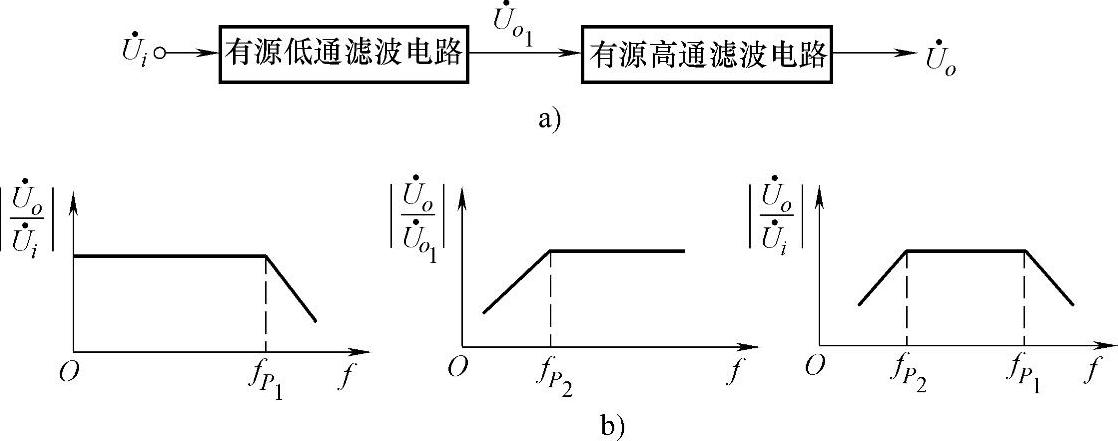
图3-25 带通滤波电路的组成及相应幅频特性曲线

a）电路 b）幅频特性

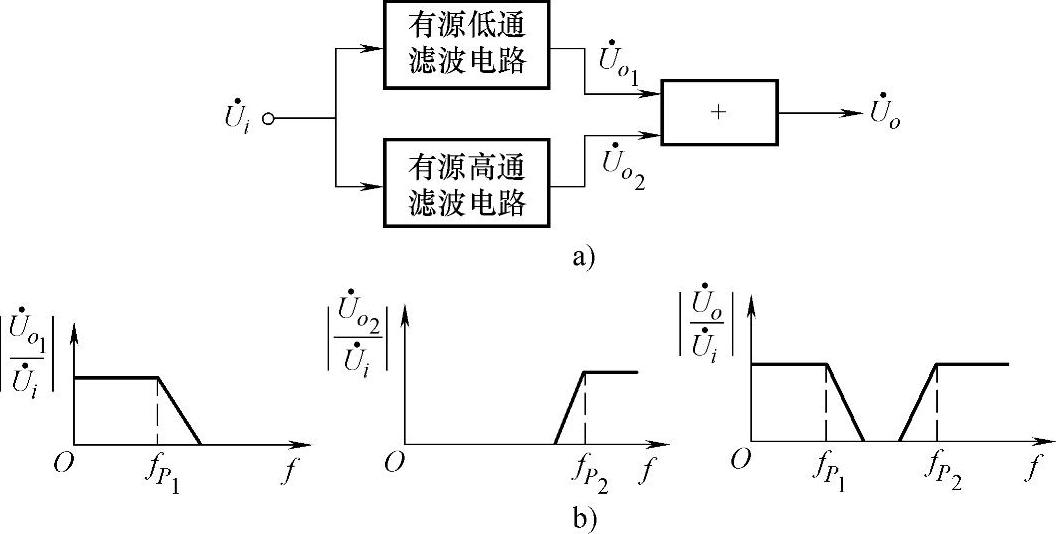
图3-26 带阻滤波电路的组成及相应幅频特性曲线

a）电路 b）幅频特性