信号运算电路实现多种数学运算方法

（1）比例放大电路

1）反相比例放大电路

图3-4所示为反相比例放大电路。输入信号u_i经过电阻R₁加到集成运算放大器的反相端，反馈电阻R_F接在输出端和反相输入端之间，构成电压并联负反馈，则集成运算放大器工作在线性区；同相端加平衡电阻R₂，主要是使同相端与反相端外接电阻相等，即R₂=R₁//R_F，以保证运算放大器处于平衡对称的工作状态，从而消除输入偏置电流及其温度漂移的影响。

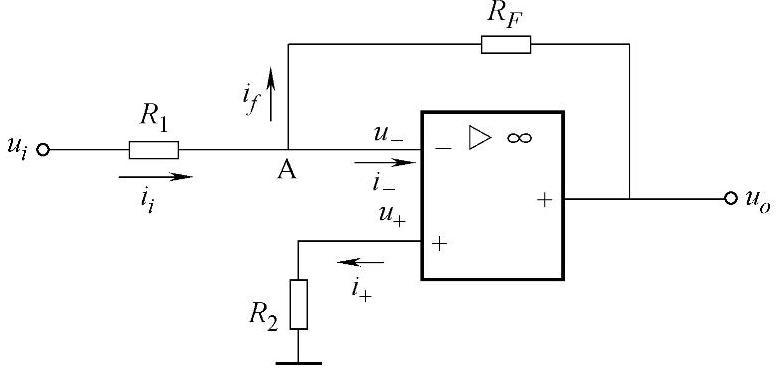
图3-4 反相比例放大电路

根据虚断的概念，i₊=i_-≈0，得u₊=0，i_i=i_f。又根据虚短的概念，u_-≈u₊=0，故称A点为虚地点。虚地是反相输入放大电路的一个重要特点。又因为有

所以有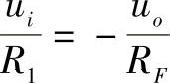移项后得电压放大倍数

式（3-4）表明，电压放大倍数与R_F成正比，与R₁成反比，式中负号表明输出电压与输入电压相位相反。当R₁=R_F=R时，u_o=-u_i，输入电压与输出电压大小相等、相位相反，反相比例放大电路成为反相器。

2）同相比例放大电路

图3-5所示为同相比例放大电路。输入信号u_i经过电阻R₂接到集成运算放大器的同相端，反馈电阻接到其反相端，构成了电压串联负反馈。根据虚断概念，i₊≈0，可得u₊=u_i。又根据虚短概念，有u₊≈u_-，于是有

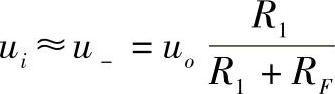
移项后得电压放大倍数

或

当R_F=0或R₁→∞时，如图3-6所示，此时u_o=u_i，即输出电压与输入电压大小相等、相位相同，该电路称为电压跟随器。

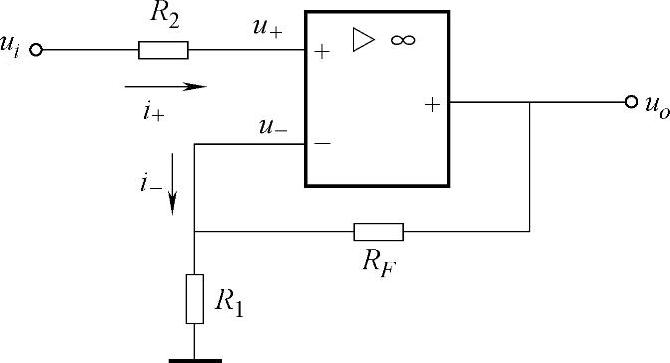
图3-5 同相比例放大电路

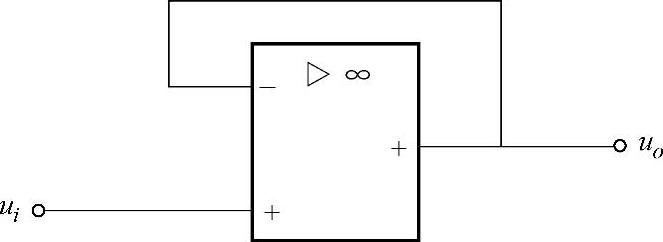
图3-6 电压跟随器

例3-1 电路如图3-7所示，试求当R₅的阻值为多大时，才能使u_o=-55u_i。

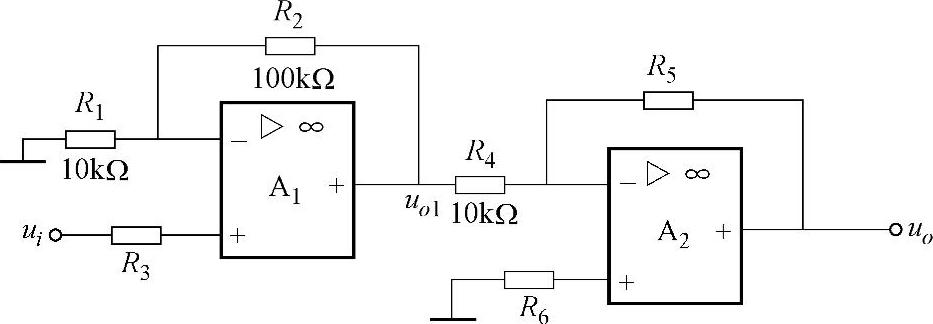
图3-7 例3-1的电路图

解：在图3-7电路中，A₁构成同相比例放大电路，A₂构成反相比例放大电路，因此有

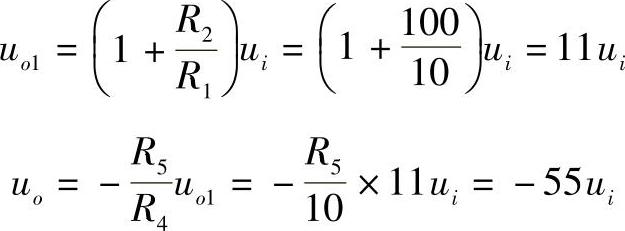
化简后得R₅=50kΩ。

（2）加、减法运算电路

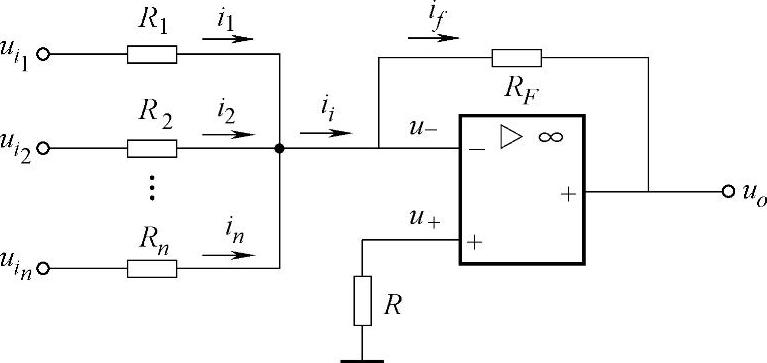
图3-8 加法运算电路

1）加法运算电路

在自动控制电路中，往往需要将多个采样信号按一定的比例叠加起来输入到放大电路中，这就需要用到加法运算电路，如图3-8所示。根据虚断的概念及结点电流定律，可得i_f=i_i=i₁+i₂+…+i_n。再根据虚短的概念可得

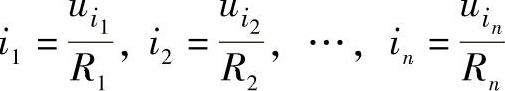
则输出电压为：

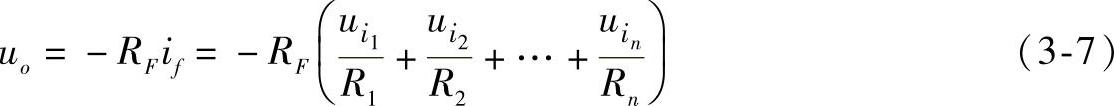
式（3-7）实现了各信号的比例加法运算。如取R₁=R₂=…=R_n=R_F，则有

2）减法运算电路

①利用反相求和实现减法运算，其电路如图3-9所示。第一级为反相比例放大电路，若取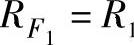，则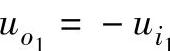。第二级为反相加法运算电路，可导出：

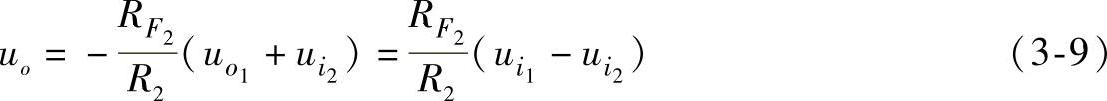
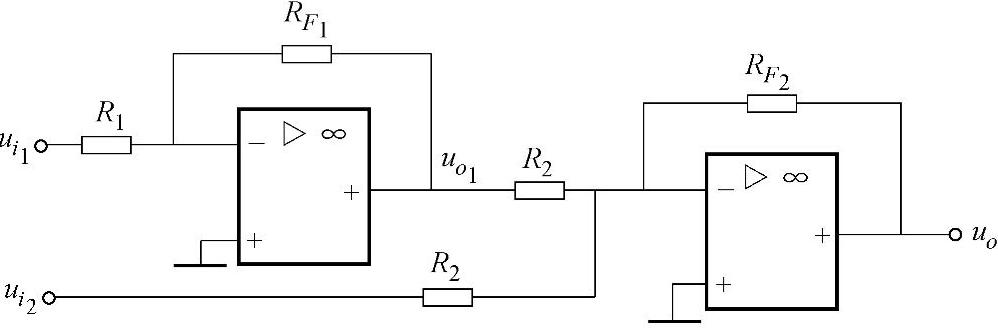
图3-9 利用反相求和实现减法运算电路

若取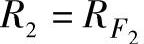，则有：

即实现了两信号的减法运算。

②利用差分式电路实现减法运算，其电路如图3-10所示。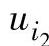经R₁加到反相输入端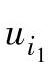，经R₂加到同相输入端。根据叠加定理，首先令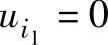，当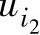单独作用时，电路成为反相放大电路，其输出电压为

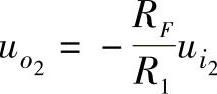
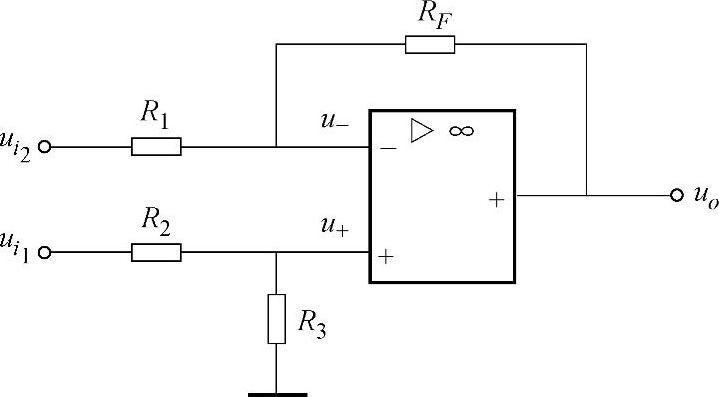
图3-10 利用差分式电路实现减法运算

再令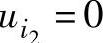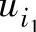，单独作用时，电路成为同相放大电路，同相端电压为

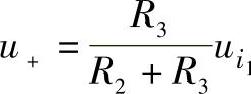
则输出电压为(www.xing528.com)

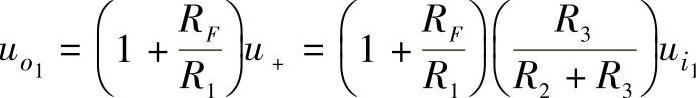
这样，当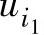和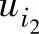同时输入时，有：

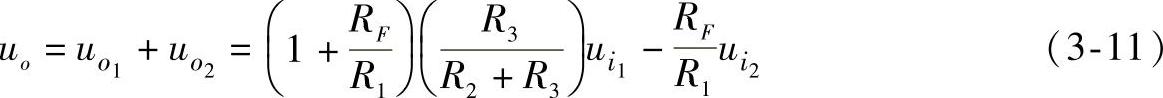
若取R₁=R₂=R₃=R_F时，有：

即实现了两信号的减法运算。

例3-2 加减法运算电路如图3-11所示，求输出与各输入电压之间的关系。

解：本题输入信号共有四个，可利用叠加法求解。

①当u_i1单独输入、其他输入端接地时，有。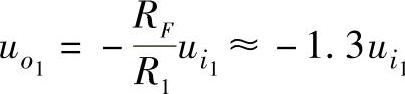

②当u_i2单独输入、其他输入端接地时，有。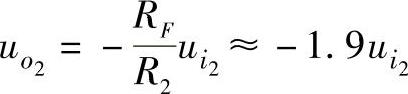

③当u_i3单独输入、其他输入端接地时，有。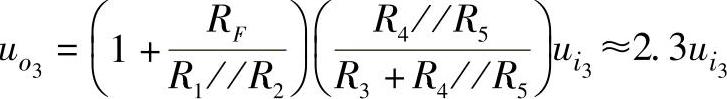

④当u_i4单独输入、其他输入端接地时，有。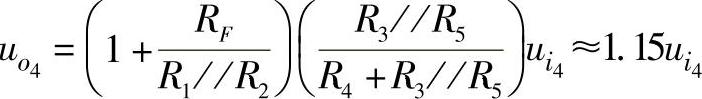

由此可得到。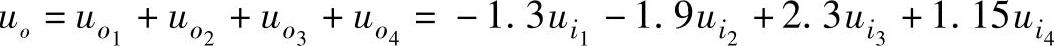

（3）积、微分运算电路

1）积分运算电路

图3-12所示为积分运算电路。根据虚地的概念，u_A≈0，i_R=u_i/R。再根据虚断的概念，有i_c≈i_R，即电容C以i_c=u_i/R进行充电。假设电容C的初始电压为零，那么

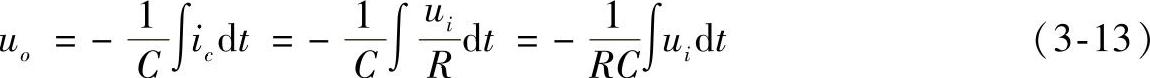
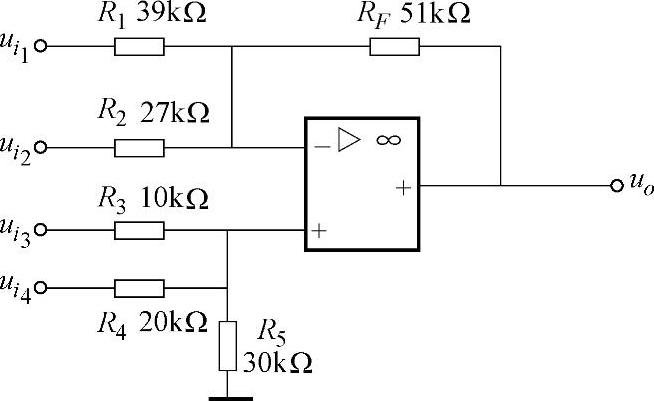
图3-11 例3-2的电路图

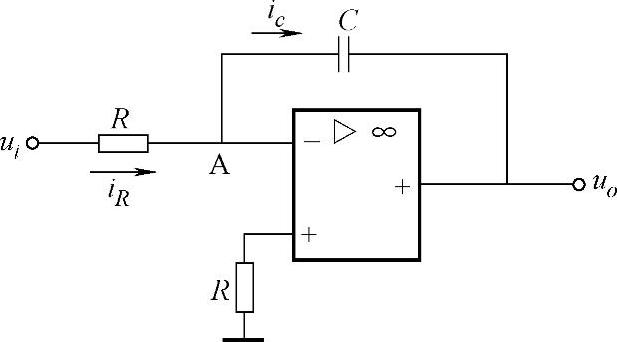
图3-12 积分运算电路

式（3-13）表明，输出电压正比于输入电压对时间的积分，且相位相反。当求解t₁到t₂时间段的积分值时，有

式（3-14）中，u_o（t₁）为积分起始时刻t₁的输出电压，即积分的起始值；积分的终值是t₂时刻的输出电压。当u_i为常量U_i时，有

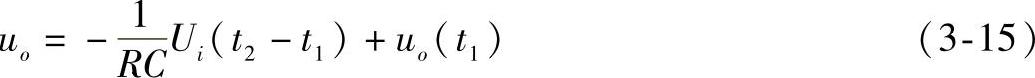
积分电路的波形变换作用如图3-13所示。当输入为阶跃波时，若t₀时刻电容上的电压为零，则输出电压波形如图3-13a所示。当输入为方波和正弦波时，输出电压波形分别如图3-13b和3-13c所示。

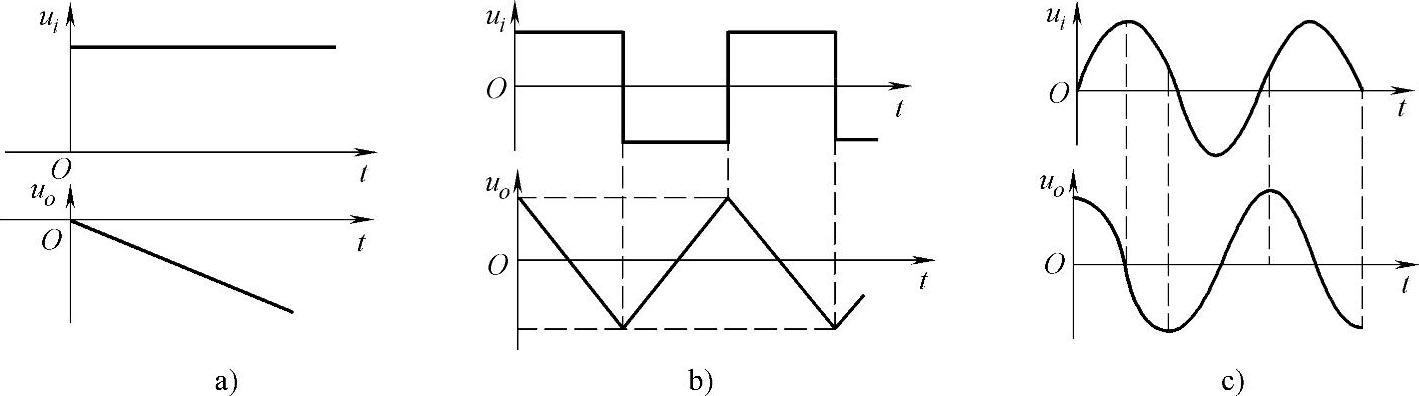
图3-13 积分电路的波形变换作用

a）输入为阶跃波 b）输入为方波 c）输入为正弦波

例3-3 电路及输入电压分别如图3-14a和3-14b所示，电容器C的初始电压u_c（0）=0，试画出输出电压u_o稳态的波形，并标出u_o的幅值。

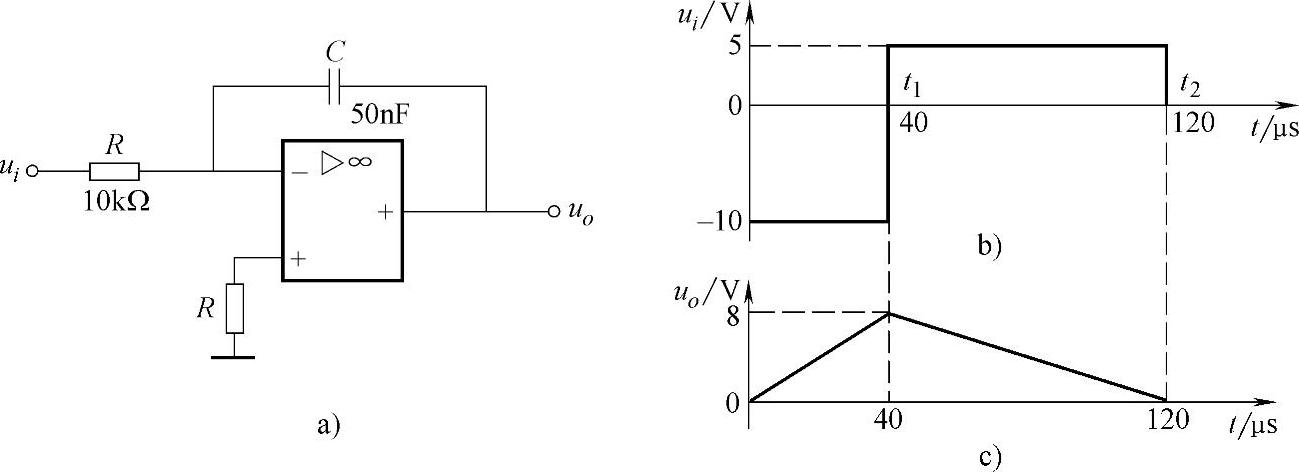
图3-14 例3-3的电路及输入/输出电压图

解：当t=t₁=40μs时，有

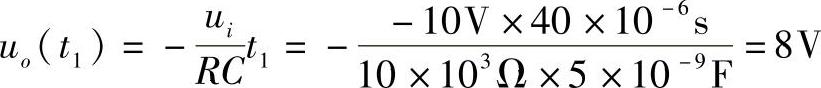
当t=t₂=120μs时，有

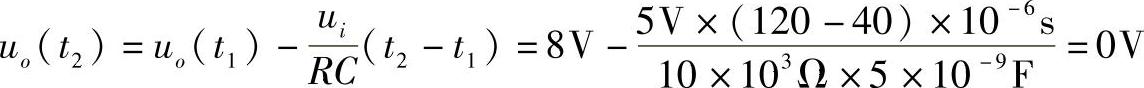
得输出波形如图3-14c所示。

2）微分运算电路

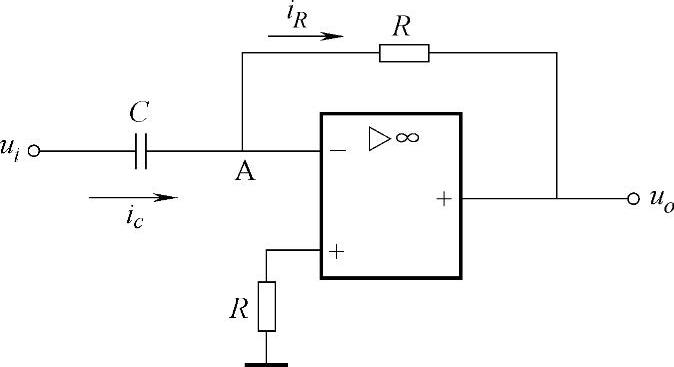
图3-15 微分运算电路

将积分电路中的R和C位置互换，就可得到微分运算电路，如图3-15所示。在这个电路中，A点为虚地，即u_A≈0。再根据虚断的概念，则有i_R≈i_c。假设电容C的初始电压为零，那么有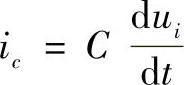，则输出电压为：

式（3-16）表明，输出电压正比于输入电压对时间的微分，且相位相反。

但如图3-15所示的电路实用性差，当输入电压产生阶跃变化时，i_c电流极大，会使集成运算放大器内部的放大管进入饱和或截止状态，使输入信号消失，放大管仍不能恢复到放大状态，也就是电路不能正常工作。同时，由于反馈网络为滞后移相，它与集成运算放大器内部的滞后附加移相相加，易满足自激振荡条件，从而使电路不稳定。

实用微分电路如图3-16a所示，它在输入端串联了一个小电阻R₁，以限制输入电流；同时在R上并联稳压二极管，以限制输出电压，这就保证了集成运算放大器中的放大管始终工作在放大区内。另外，在R上并联小电容C₁，起相位补偿作用。该电路的输出电压与输入电压近似为微分关系，当输入为方波，且RC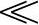T/2时，则输出为尖顶波，波形如图3-16b所示。

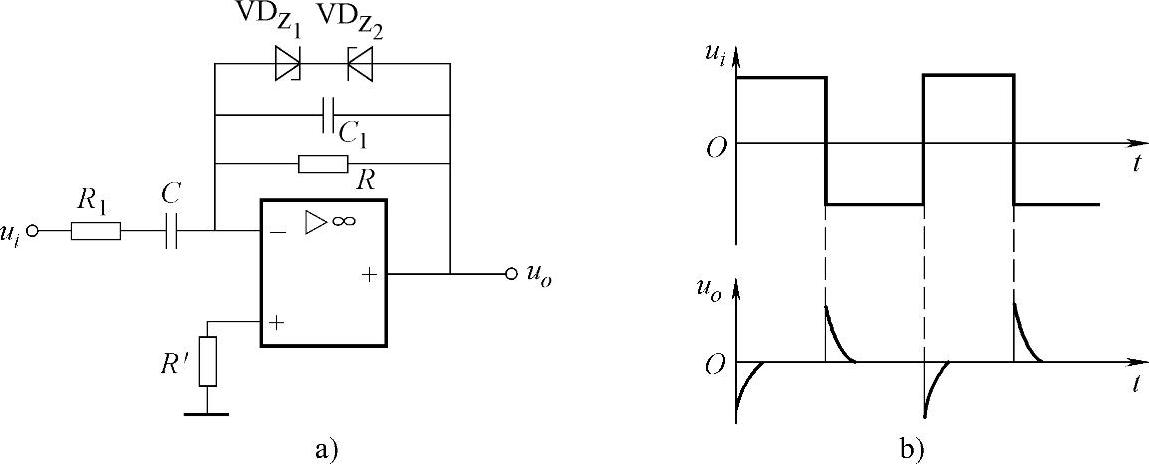
图3-16 实用微分电路及输入/输出电压波形

a）实用微分电路 b）输入和输出波形