工业机器人的高效控制技术

控制系统是机器人的重要组成部分，使机器人按照指令要求去完成所希望的作业任务。如图4-4所示，机器人控制系统通常包括控制计算机、示教盒、操作面板、存储器、检测传感器、输入输出接口、通信接口等部分。

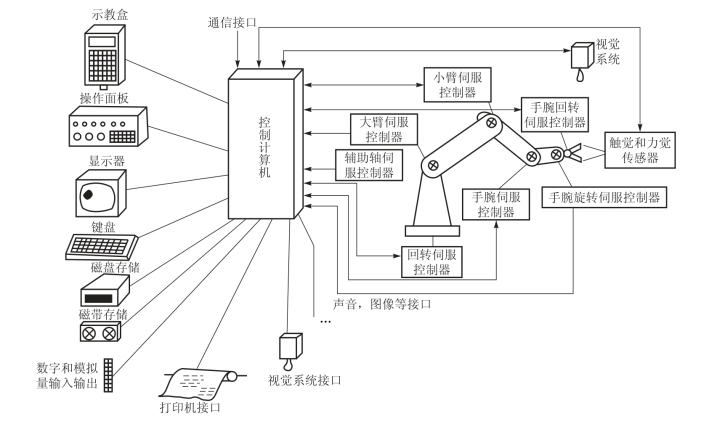
图4-4　工业机器人控制系统的组成框图

1.工业机器人控制系统的分类

由于机器人的类型较多，其控制系统的形式也是多种多样。

1）按照控制回路的不同分，可将机器人控制系统分为开环系统和闭环系统。闭环系统比开环系统多了一个检测反馈装置。对于闭环系统而言，由系统发出一个位置控制指令，它与来自位置传感器的反馈信号进行比较，得到一个位置差值，将其差值加以放大驱动伺服电动机，控制机器人完成相应的运动和动作。

2）按照控制系统的硬件分，有机械控制、液压控制、射流控制、顺序控制和计算机控制等。自20世纪80年代以来，机器人的控制一般采用了计算机控制形式。

3）按自动化控制程度分，机器人控制系统又分为顺序控制系统、程序控制系统、自适应控制系统、人工智能系统。

4）按编程方式分，有物理设置编程控制系统、示教编程控制系统、高线编程控制系统。所谓物理设置编程控制是由操作者设置固定的限位开关，实现启动、停车的程序操作，用于简单的抓取和放置作业；示教编程控制是通过人的示教来完成操作信息的记忆，然后再现示教阶段的动作过程；离线编程控制是通过机器人语言进行编程控制。

5）按机器人末端运动控制轨迹分，有点位控制和连续轮廓控制之分。在点位控制中，机器人每个运动轴单独驱动，不对机器人末端操作的速度和运动轨迹作出要求，仅要求实现各个坐标的精确控制。机器人的轮廓控制与CNC系统有所不同，在机器人控制系统中没有插补器，在示教编程时要求将机器人轮廓轨迹运动中的各个离散坐标点以及运动速度同时存储于控制系统存储器，再现时按照存储的坐标点和速度控制机器人完成规定的动作。

2.工业机器人的位置伺服控制

图4-5给出了机器人位置伺服控制系统的构成示意图。对于机器人运动，常关注的是手臂末端的运动，而末端运动往往又是以各关节的合成来实现的，因而必须关注手臂末端的位置和姿态与各关节位移的关系。在控制装置中，手臂末端运动的指令值与手臂的反馈信息作为伺服系统的输入，不论机器人采用什么样的结构形式，其控制装置都是以各关节当前位置q和速度q′作为检测反馈信号，直接或间接地决定伺服电动机的电压或电流向量，通过各种驱动机构达到位置矢量r控制的目的。

图4-5　刚性臂控制系统的构成

机器人的位置伺服控制，大体上可分为关节伺服和坐标伺服两种类型。

（1）关节伺服控制(www.xing528.com)

关节伺服控制是以大多数非直角坐标机器人为控制对象。图4-6给出了关节伺服控制的构成，它把每一个关节作为单独的单输入单输出系统来处理。令各关节位移指令目标值为qd=［qd1，qd2，…，qdn］T，且独立构成一个个伺服系统。每个指令目标值qd与实际末端位置值rd都存在对应关系：qd=R（rd）。对于每一个末端位置rd，均能求取一个指令值qd与之对应。这种关节伺服系统结构十分简单，目前大部分关节机器人都由这种关节伺服系统来控制。以往这类伺服系统通常用模拟电路构成，而随着微电子和信号处理技术的发展，已普遍采用了数字电路形式。

图4-6　关节伺服控制的构成

（2）坐标伺服控制

尽管关节伺服控制结构简单，被较多的机器人所采用，但在三维空间对手臂进行控制时，很多场合都要求直接给定手臂末端运动的位置和姿态，例如将手臂从某一点沿直线运动到另一点就是这种情况。此外，关节伺服控制系统中的各个关节是独立进行控制的，难以预测由各关节实际控制结果所得到的末端位置状态的响应，且难以调节各关节伺服系统的增益。因而，将末端位置矢量rd作为指令目标值所构成的伺服控制系统，称为作业坐标伺服系统。这种伺服控制系统是将机器人手臂末端位置姿态矢量rd固定于空间内某一个作业坐标系来描述的。

3.工业机器人的自适应控制

自适应控制是由Dubowsky等于1979年用于机器人的。至20世纪80年代中期，在机器人控制领域基本形成了模型参考自适应控制和自校正适应控制两种流派。

（1）模型参考自适应控制

这种方法控制器的作用是使得系统的输出响应趋近于某指定的参考模型，因而必须设计相应的参数调节机构，如图4-7所示。Dubowsky等在这个参考系统中采用二维弱衰减模型，然后采用最陡下降法调整局部比例和微分伺服可变增益，使实际系统的输出和参考模型的输出之差为最小。然而，该方法从本质上忽略了实际机器人系统的非线性项和耦合项，是对单自由度的单输入单输出系统进行设计的。此外，该方法也不能保证用于实际系统时调整律的稳定性。

（2）自校正适应控制

在自适应控制方法中，除模型参考自适应之外，还有自校正方法。如图4-8所示，这种方法由表现机器人动力学离散时间模型各参数的估计机构与用其结果来决定控制器增益或控制输入的部分组成，采用输入输出数与机器人自由度相同的模型，把自校正适应控制法用于机器人。

图4-7　模型参考自适应控制系统

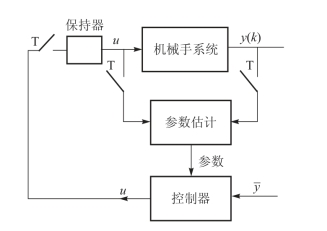
图4-8　自校正适应控制系统