矩阵基础：行列式、单位矩阵和逆矩阵

A.1 矩阵的定义

1.矩阵的定义

m×n阶矩阵是一个有m行和n列的长方形数表，用符号A来表示

矩阵中的每个数a_jk称为矩阵元，矩阵元的下标j和k分别指明该元素位于矩阵中的行号和列号。

2.矩阵相等

两个同阶的矩阵A和B，当且仅当a_jk=b_jk时相等。A.2 矩阵的运算

1.矩阵加法

若A和B矩阵有相同的阶，则矩阵加法C=A+B的运算为

C=A+B=（a_jk+b_jk）

矩阵相加的公式说明：相同位置的矩阵元相加的和为和矩阵的矩阵元。

2.数与矩阵相乘

若矩阵A=（a_jk），而λ为任一常数，则矩阵A乘以λ的定义为

C=λA=λ（a_jk）

数与矩阵相乘的公式说明：数乘矩阵元的积为数乘矩阵的矩阵元。

3.矩阵与矩阵相乘

若矩阵A=（a_jk）的列数与矩阵B=（b_jk）的行数相等，则矩阵A乘以B的定义为

注意：矩阵相乘不满足交换律，即AB≠BA。

4.矩阵的转置

把一个矩阵A的行和列交换以后所得到的矩阵称为矩阵A的转置，用符号A^T来表示。即，A=（a_kj），则，A^T=（a_kj）。

例如，，则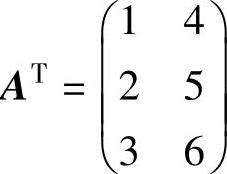A.3 行列式

如果矩阵A是一个方阵，则同A相联系的一个数Δ为

称为A的n阶行列式。对于一个2×2的矩阵A的行列式为(www.xing528.com)

A.4 单位矩阵和逆矩阵

1.单位矩阵

一个方阵如果主对角线上的所有元素都是1，其余的元素都是0，则该矩阵称为单位矩阵，用符号I来表示。

单位矩阵在矩阵代数中所起的作用类似于数1在普通代数中所起的作用。

2.逆矩阵

若给定的方阵A，存在一个矩阵B，使得AB=I，则称B是A的逆（矩阵），用符号A^-1来表示，用行列式和余因子的概念还可以将A^-1表示成下面的形式：

A.5 线性方程组和矩阵

1.将方程组写成矩阵

形如

的方程组是有n个未知数x₁，x₂，x₃，…，x_n的m个线性方程的组，若r₁，r₂，r₃，…，r_n全部为零，则称方程组是齐次的，如果不全部为零，就称为非齐次的，任何一组满足方程组的x₁，x₂，x₃，…，x_n称为方程组的解。线性方程组可以表示成矩阵

或简写为

AX=R

2.解方程组的克拉默法则

若m=n，在A^-1存在的条件下，线性方程组的解为

X=A^-1R

根据逆矩阵和余因子的公式可得

式中的Δ_k（k=1，2，3…，n）是用列向量R替换Δ中的第k个列向量后所得到的行列式，上述求解未知数的公式就是克拉默法则。

例如，已知二端口网络的Z参数方程为

根据克拉默法则可得电流i₁和i₂的解为

在电路分析的课程中所用到的矩阵知识主要就是这些，关于矩阵的运算可以用MATLAB编程来实现。