谐振功率放大器余弦脉冲电流分解优化研究

在图11-12中，设输入信号为

u_i=U_mcos（ωt）

则基极回路的电压为

u_be=U_be+u_i=U_bb+U_mcos（ωt） （11-13）

在U_bb=0、U_on=0的前提下，图11-12所示电路的集电极电流信号的波形与乙类放大器相同，都是如图11-2所示的单向脉动信号，导通角为180°。在U_bb等于负值，且U_on也不等于0，并用折线代替晶体管输入特性曲线的情况下，图11-12所示电路的集电极电流信号的波形，虽然还是单向脉动信号，但导通角小于180°，如图11-13所示。

设在图11-13中，晶体管输入特性曲线的折线斜率为g，电流放大倍数为β，折线起点处的电压为U_on，根据图11-13所示的折线可得集电极电流的表达式为

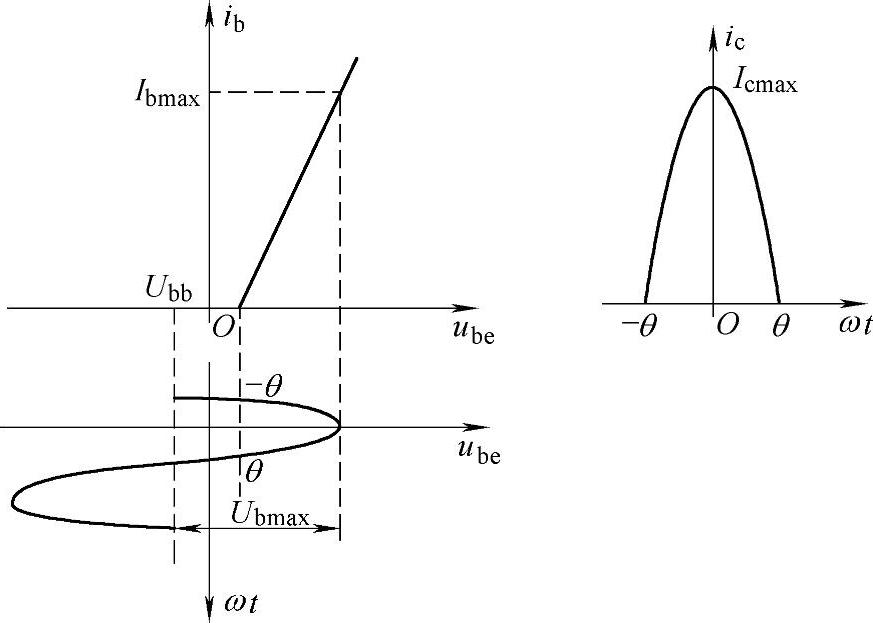
图11-13 集电极电流的波形

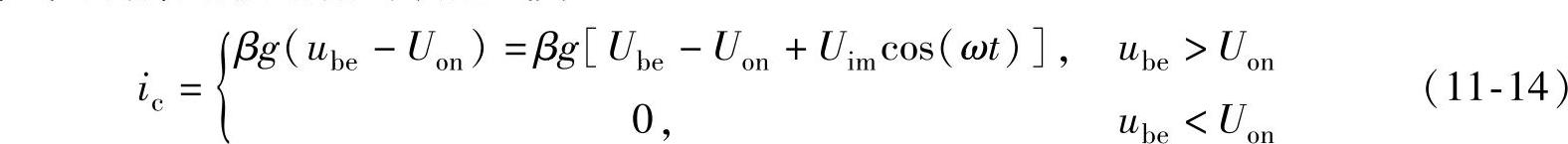
在图11-13中，i_c=0的点对应的ωt=±θ，将该结论代入式（11-14）中可得

将式（11-15）代入式（11-14）可得集电极电流的表达式为

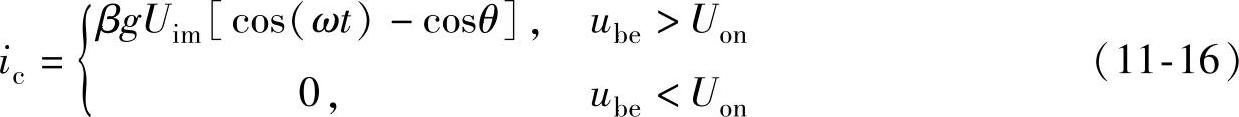
ωt=0的点，对应于集电极电流的最大值I_cmax，根据式（11-16）可得I_cmax为

I_cmax=βgU_im（1-cosθ） （11-17）

将式（11-17）代入式（11-16）可得集电极电流的表达式为

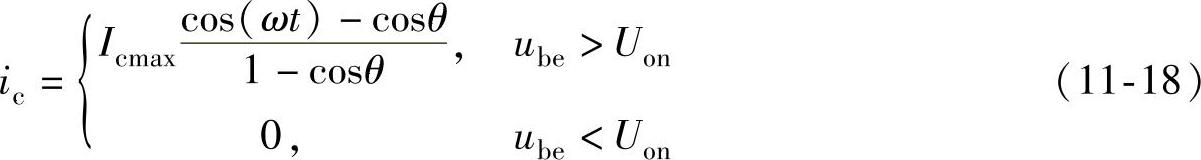
式（11-18）的波形是如图11-13所示的余弦脉动电流，随着周期信号的输入，式（11-18）所表示的余弦脉动电流也呈现出周期性，利用傅里叶级数的理论可以将式（11-18）写成傅里叶级数的形式为(www.xing528.com)

式中的I_c0、I_c1、I_c2、I_cn分别称为余弦脉冲的直流、基波和n次谐波的系数。根据傅里叶级数求系数的公式可得

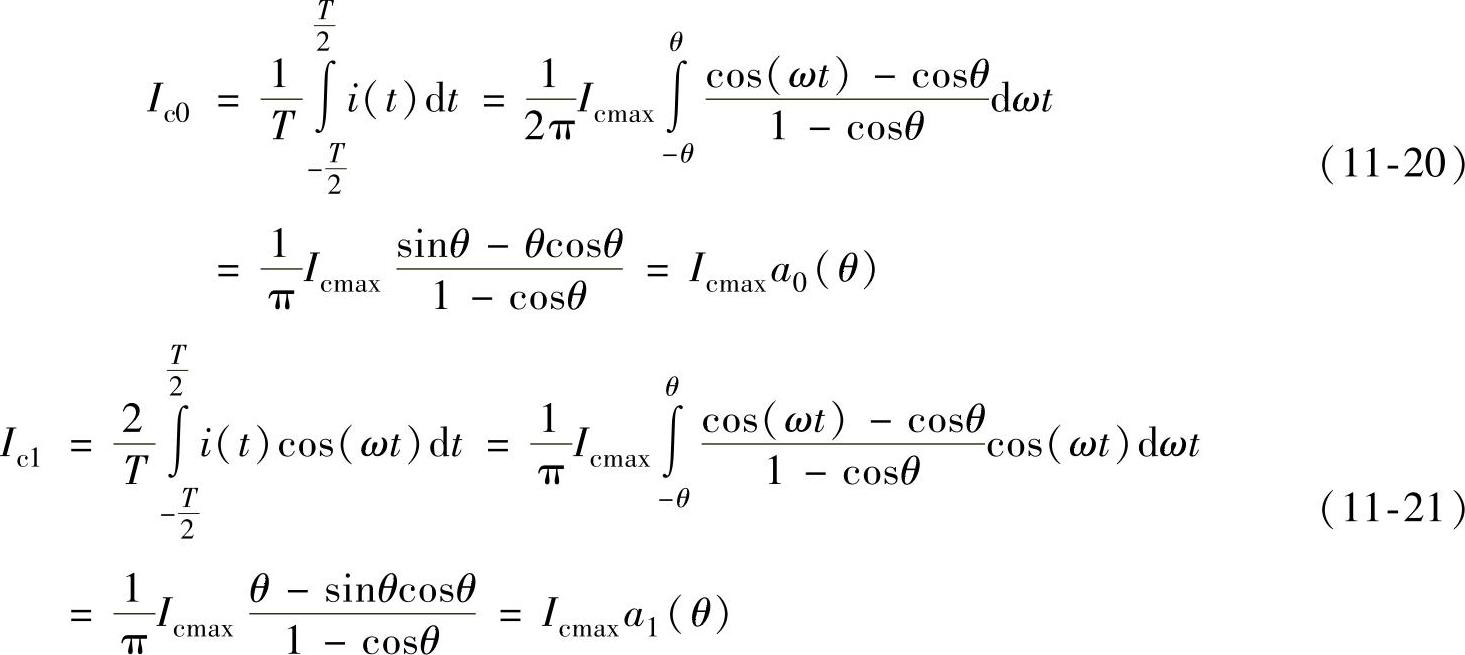
用相同的方法可以求出式（11-19）中的各项系数，用MATLAB求I_cn的程序为

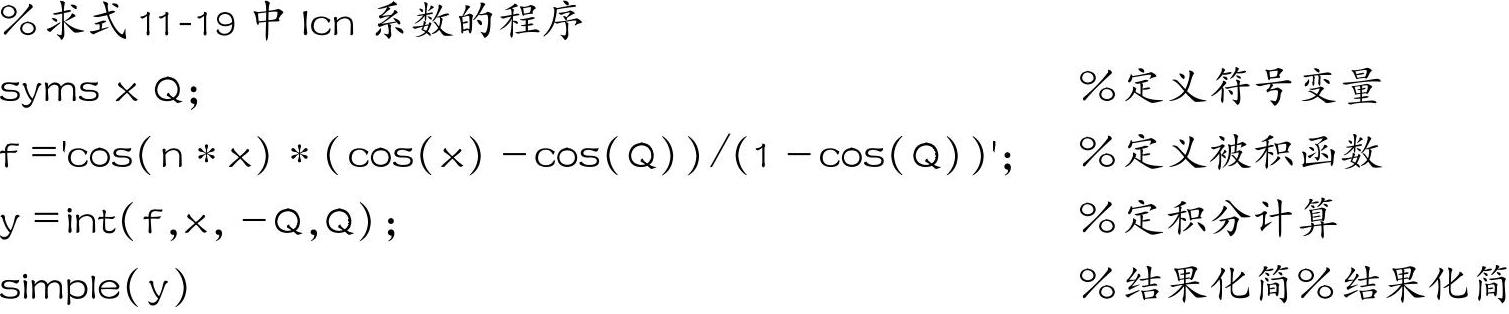
该程序运行的结果为

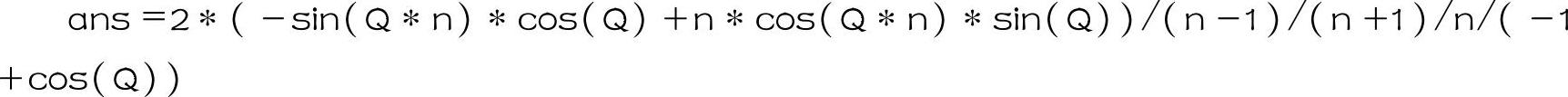
将被积函数中省略的参数代入可得I_cn的表达式为

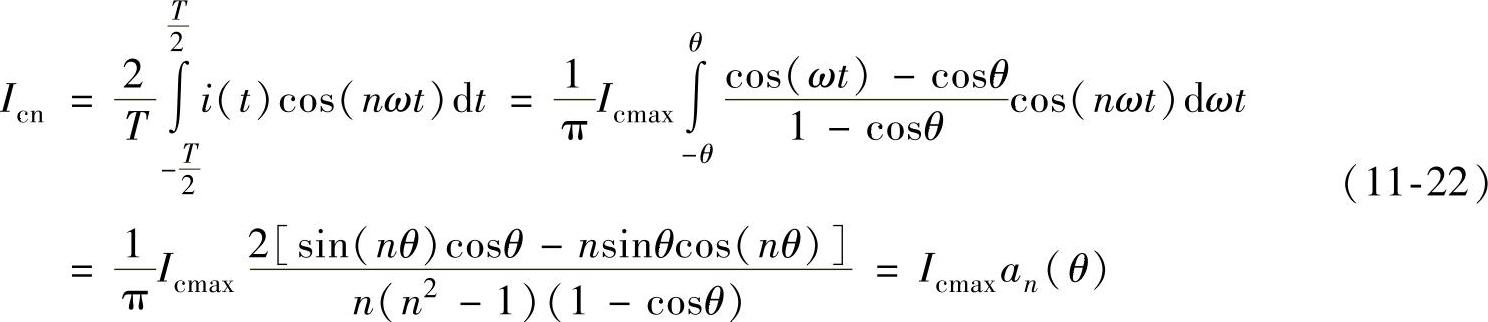
改变程序中的参数n，可求出式（11-19）中各次谐波的系数，当n=1时，计算谐波系数的程序为

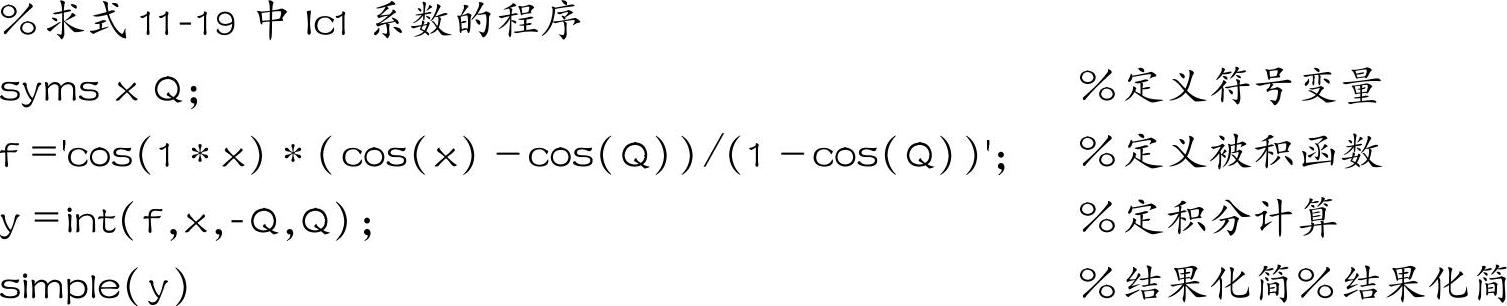
该程序运行的结果为

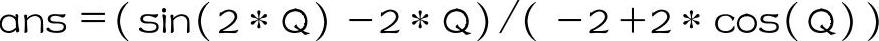
将被积函数中省略的参数代入可得I_c1的表达式为

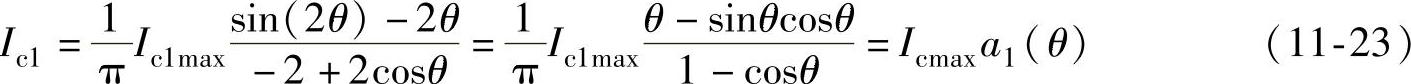
式（11-23）与式（11-21）相同。式中的a（θ）称为余弦脉冲电流的分解系数，将θ的值代入上面的各个计算式子，可以计算出各次谐波分解系数的值，这些值已经被制成余弦脉冲分解系数表，感兴趣的读者可参阅相关的参考书。