正弦波振荡器电路的构成优化

1.产生正弦振荡的条件

负反馈放大器的组成框图如图9-1所示，根据负反馈放大器的知识可知，在电路中引入负反馈，可以改变放大器的放大倍数，负反馈对放大器放大倍数影响的关系满足下式：

在式（9-1）中，若-1＜AF＜0，则|A_f|＞|A|，即闭环放大倍数大于开环放大倍数，说明负反馈放大器变成了正反馈放大器。特别是当AF=-1时，反馈放大器的闭环放大倍数|A_f|=∞，此时的放大器在没有输入信号的情况下，仍然有输出信号输出，反馈放大器将转变成振荡器。由此可得反馈放大器产生振荡要满足的条件是

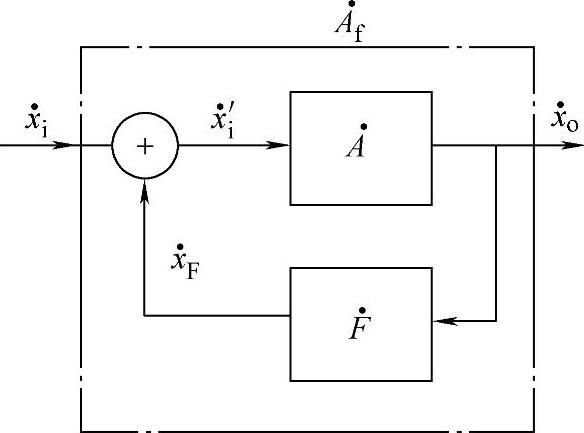
图9-1 负反馈放大器的组成框图

ϕ=ϕ_A+ϕ_F=2nπ （9-2）

AF=-1 （9-3）

式（9-2）称为反馈放大器产生振荡的相位条件，式中的ϕ_A为基本放大器的相移，ϕ_F为反馈网络的相移，两个相移的和为2nπ，说明反馈放大器在引入正反馈之后有可能成为振荡器，该条件是振荡器产生振荡的必要条件。

式（9-3）称为反馈放大器产生振荡的振幅条件，说明反馈放大器在引入正反馈之后要产生振荡，环路放大倍数的值要满足的条件，该条件是振荡器产生振荡的充分条件。式（9-2）和式（9-3）称为反馈放大器产生振荡的充分必要条件。

2.正弦波振荡器的组成和分类(www.xing528.com)

由上面的分析可知，反馈放大器在满足振荡的充分必要条件后将转变成振荡器，该振荡器可输出各种频率的正弦波信号。利用第2章介绍的选频网络可以从不同频率的信号中取出所需要的正弦波信号，利用稳幅网络可以稳定正弦波振荡器输出信号的幅度。

由此可得，正弦波振荡器应该由基本放大器、反馈网络、选频网络和稳幅网络4个部分组成，缺一不可。这4个部分的作用分别是：放大器和反馈网络组成正反馈放大器；选频网络用来提取特定频率的正弦波信号；稳幅网络用来稳定正弦波振荡器输出信号的幅度。在实际的振荡器电路中，反馈网络和选频网络通常是由同一个电路组成的。

根据选频网络的不同，可将正弦波振荡器分成RC正弦波振荡器、LC正弦波振荡器和石英晶体正弦波振荡器3种类型。在低频的情况下，通常用RC正弦波振荡器，在高频的情况下通常用LC正弦波振荡器，在振荡频率要求非常稳定的场合应选用石英晶体振荡器。

3.判断电路是否会产生振荡的方法

由上面的分析可知，正弦波振荡器由基本放大器、反馈网络、选频网络和稳幅网络4部分组成。且选频网络和反馈网络通常是由同一个电路组成，所以正弦波振荡器在电路组成的形式上与反馈放大器非常相似。下面来讨论如何区分反馈放大器和振荡器及判断振荡器是否会产生振荡的方法。

反馈放大器和振荡器的主要区别是反馈的极性，反馈放大器为了改善电路的性能，通常引入负反馈，而振荡器引入的反馈必须是正反馈。若给定一个电路的反馈极性是负反馈，则该电路肯定是负反馈放大器。若给定一个电路的反馈极性是正反馈，则该电路在满足式（9-3）条件的情况下是振荡电路；在不满足式（9-3）条件的情况下，是反馈放大器。

例如，在图9-2所示的电路中，有两个反馈网络，其中电阻R₁和R₂组成运算放大器的负反馈网络，电容C和电阻R的串、并联电路组成运算放大器的正反馈网络。当负反馈网络的反馈量大于正反馈网络的反馈量时，电路总的反馈是负反馈，结果为负反馈放大器；当负反馈网络的反馈量小于正反馈网络的反馈量时，电路总的反馈是正反馈，结果可能是振荡器。下面的讨论证明该电路为RC正弦波振荡器。

图9-2 RC正弦波振荡器