其他形式的滤波电路解析

1.同相输入一阶高通滤波电路

（1）电路的组成

有源高通滤波器电路的组成与低通滤波电路一样，将高通滤波器和同相比例运算放大器串接起来，即可组成一阶高通滤波器，如图8-52所示。

（2）电压放大倍数

根据高通滤波器频响特性的表达式和同相比例运算放大器电压放大倍数的表达式可得一阶高通滤波器电压放大倍数的表达式为

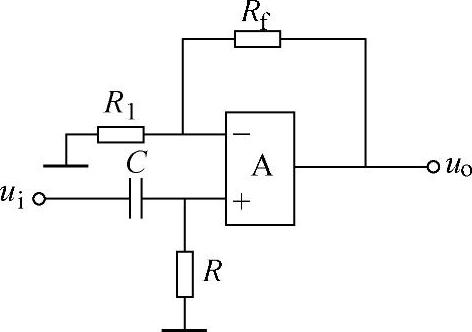
图8-52 高通滤波器

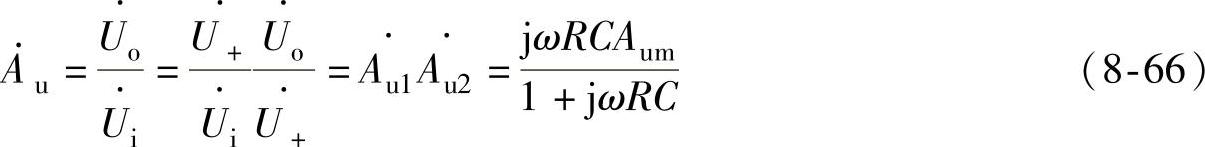
该电路的幅频特性和相频特性分别为

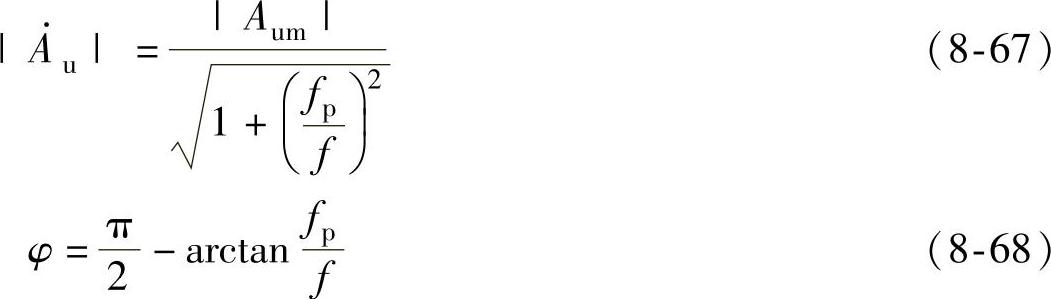
该电路的通带截止频率称为下限截止频率，用符号f_L来表示，由式（8-67）可得f_L为

将式（8-67）写成分贝的形式为

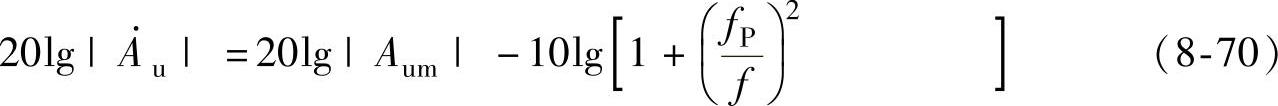
根据式（8-67）和式（8-68）也可画出有源高通滤波器的波特图，所画的波特图与第3章介绍的无源高通滤波器的波特图相类似。用仿真软件测量的有源高通滤波器的波特图如图8-53所示，用二阶滤波器同样可以改善滤波的效果。

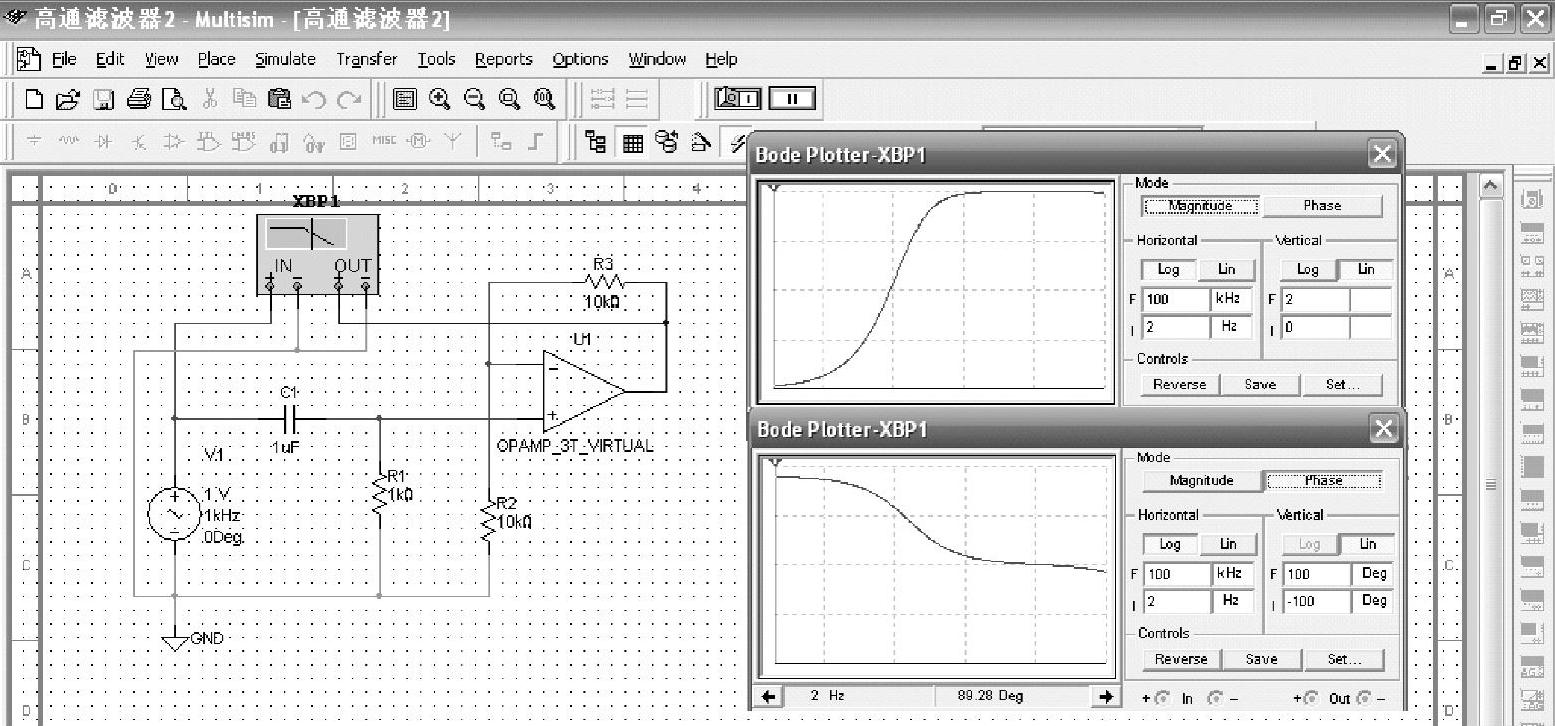
图8-53 有源高通滤波器波特图测量的结果

在图8-53中，第一个波特图屏幕上的波形是有源高通滤波器的幅频特性，第二个波特图屏幕上的波形是相频特性，这些波形清晰地显示出图8-52所示的电路是有源高通滤波器。

2.二阶高通滤波器

（1）电路的组成

将两个一阶的高通滤波器串联起来即可组成二阶高通滤波器，为了改善二阶高通滤波器的通带宽度，也是采用正反馈技术将f₀点附近的A_u值提高，形成压控电压源高通滤波器。二阶压控电压源高通滤波器的电路组成如图8-54所示。

（2）高通滤波器电压放大倍数

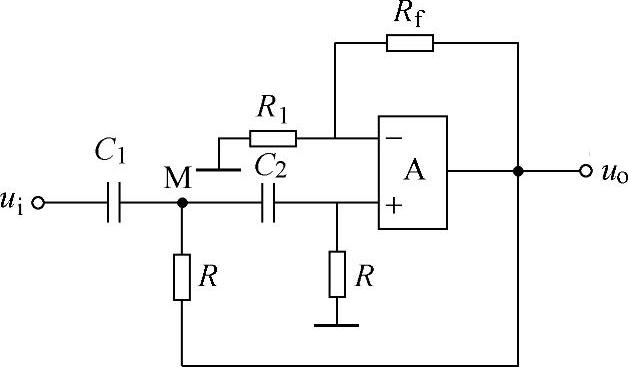
图8-54 二阶高通滤波器

为了讨论问题的方便，令C₁=C₂=C，根据“虚短”、“虚断”的概念和节点电位法可得

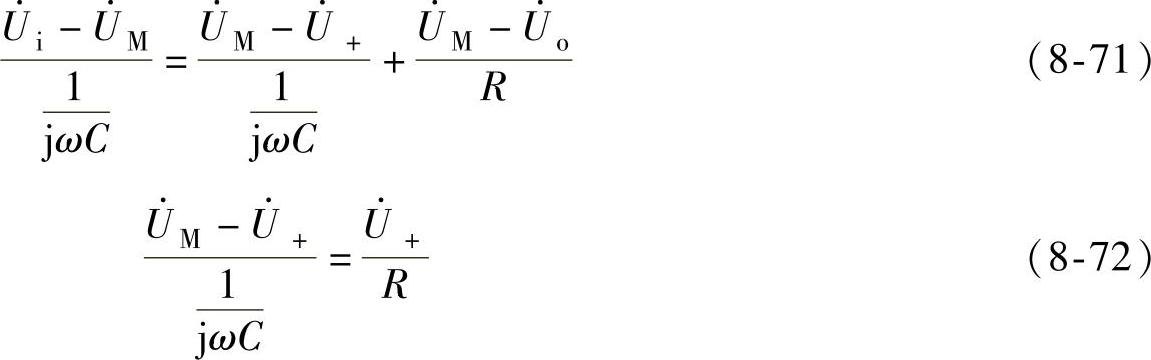
联立求解可得

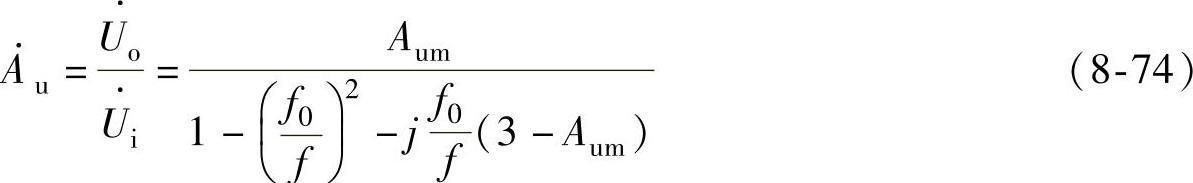
该电路的幅频特性为

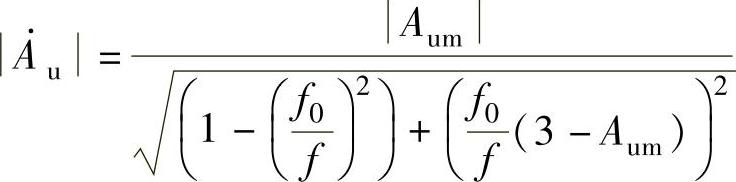
在A_um=2的情况下，用MATLAB画幅频特性曲线的程序为

该程序运行的结果如图8-55所示。

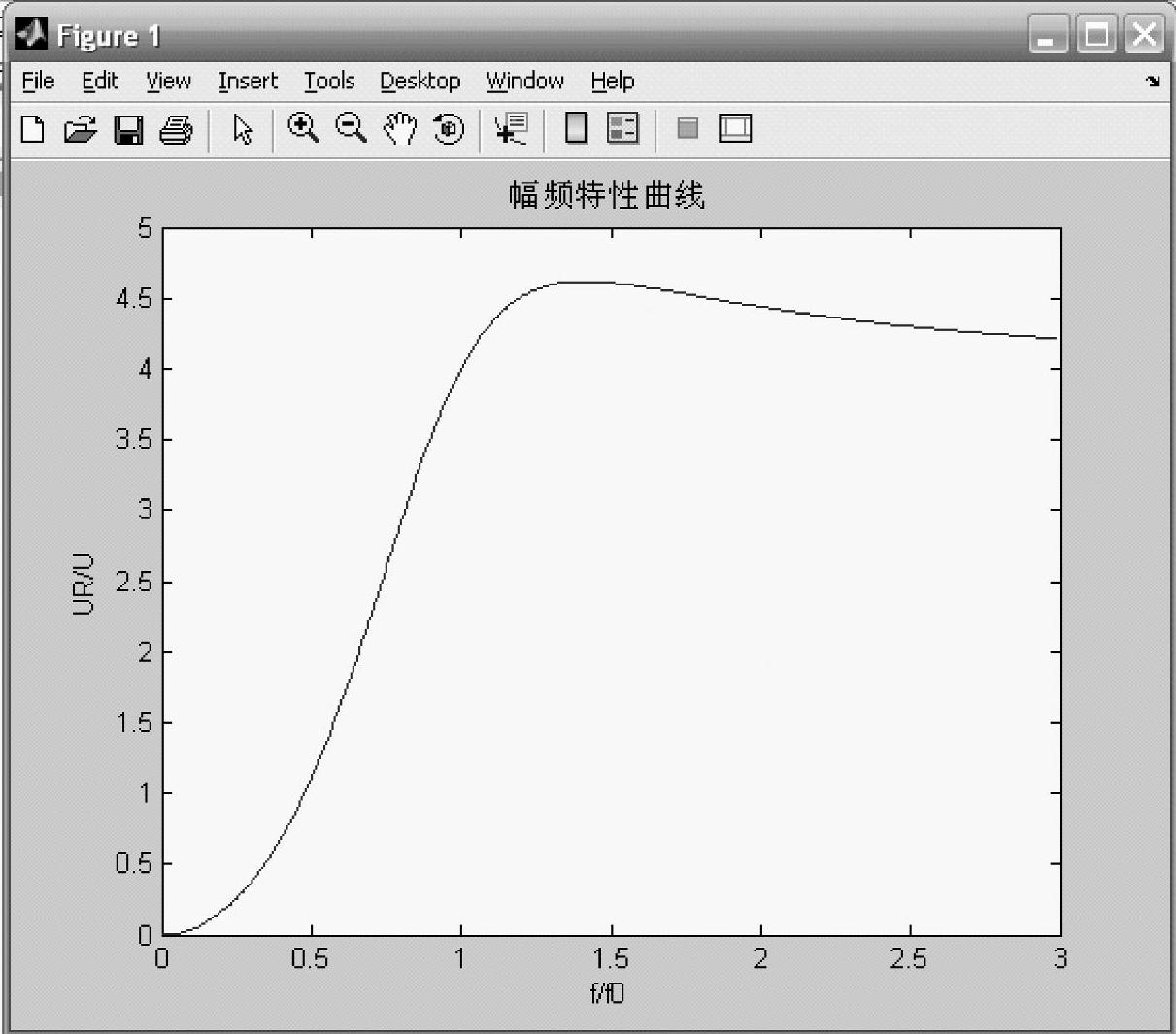
图8-55 二阶高通滤波器的幅频特性曲线

【例8-8】 求如图8-56所示电路的电压放大倍数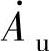，并说明该电路可实现的功能。

解 根据节点电位法和“虚短”、“虚断”的概念可得

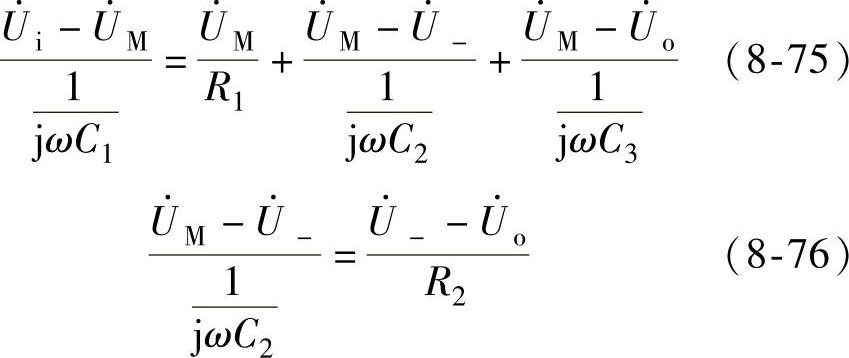
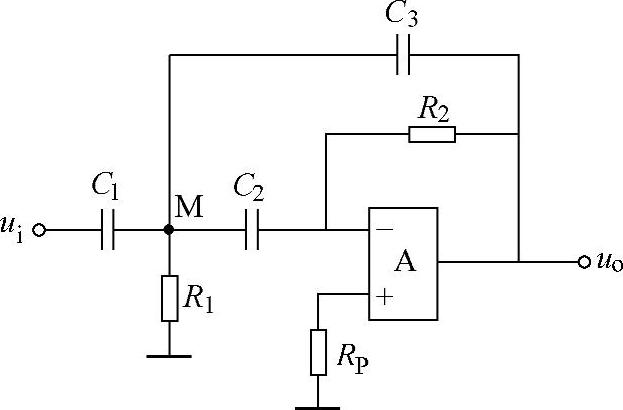
图8-56 例8-8图

联立求解得

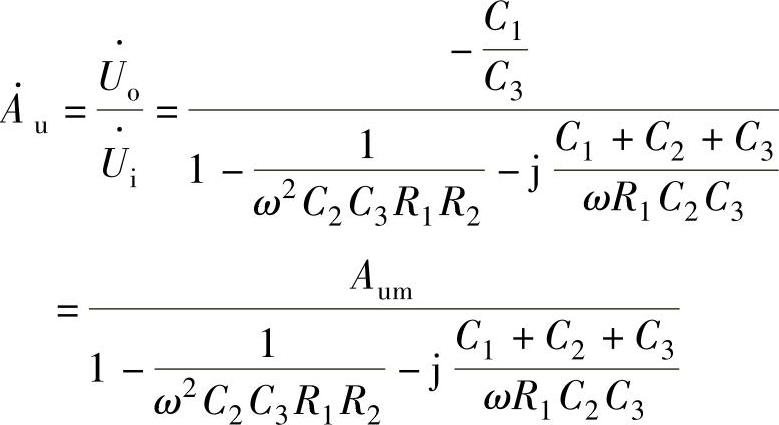
式中，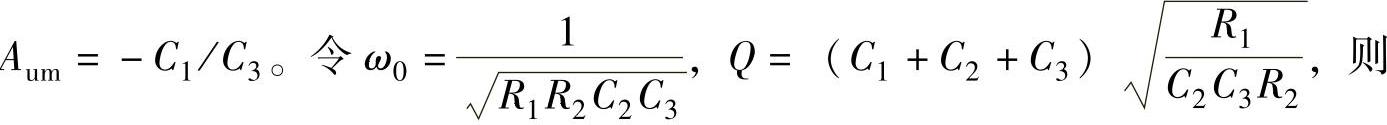

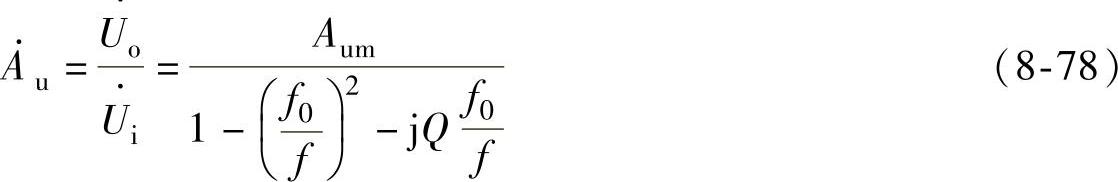
式（8-78）与式（8-74）的形式相同，说明该电路也可以实现二阶高通滤波器的功能。因为该电路的输入信号是从运算放大器的反相输入端输入的，所以该电路称为反相输入的二阶高通滤波电路。

3.带通滤波器

（1）电路的组成

允许某一段频率范围内的信号通过的电路称为带通滤波器。带通滤波器电路的组成如图8-57所示。

图8-57所示的电路说明，将低通滤波器、高通滤波器和运算放大器串联起来，即可组成带通滤波器，图8-57中的R₄为压控电压源电路的反馈网络，用来改善带通滤波器的带宽。

（2）电压放大倍数

根据节点电位法和“虚短”、“虚断”的概念可得

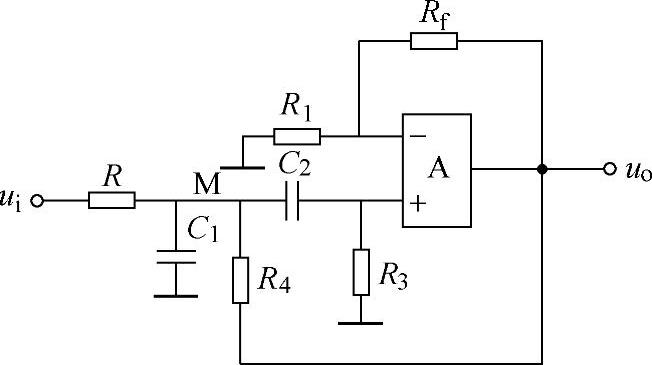
图8-57 带通滤波器

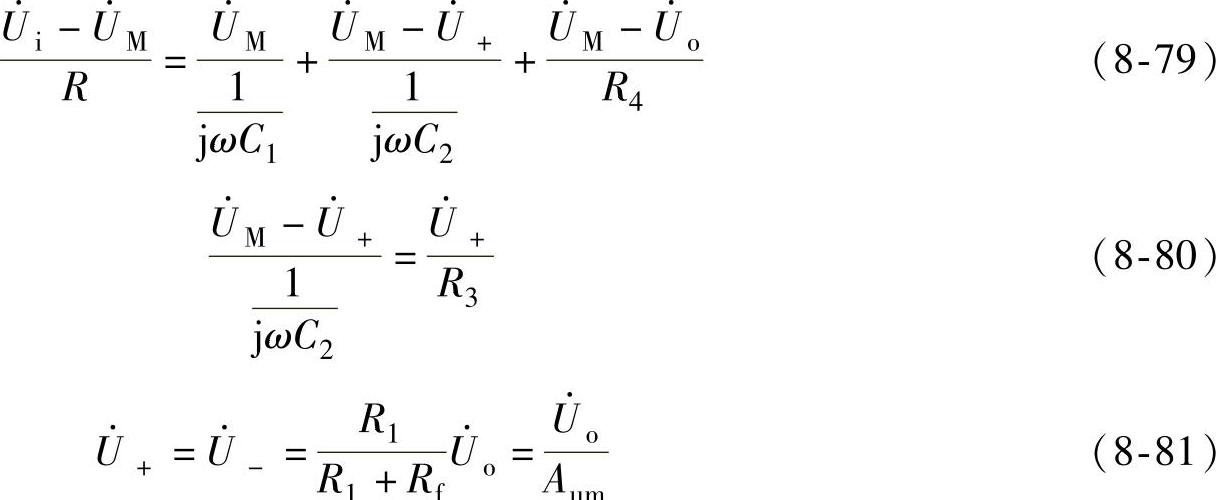
在R₃=2R，R₄=R，C₁=C₂=C的条件下，联立求解得

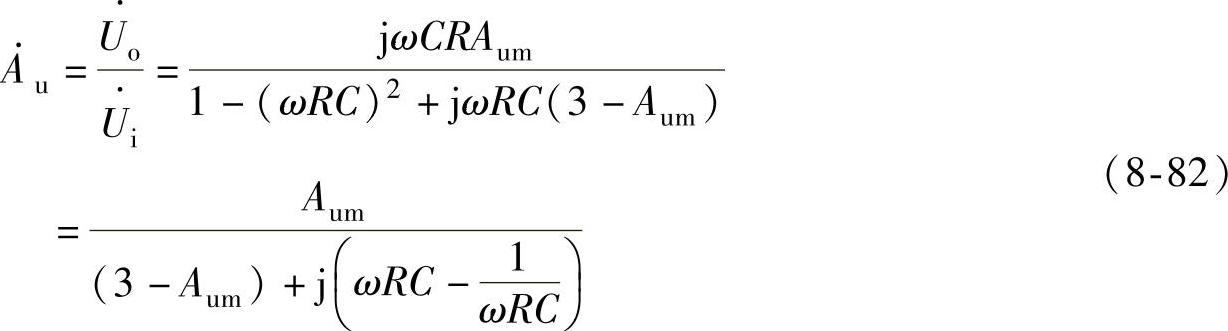
将带通滤波器中心频率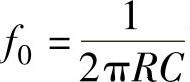的关系代入上式可得

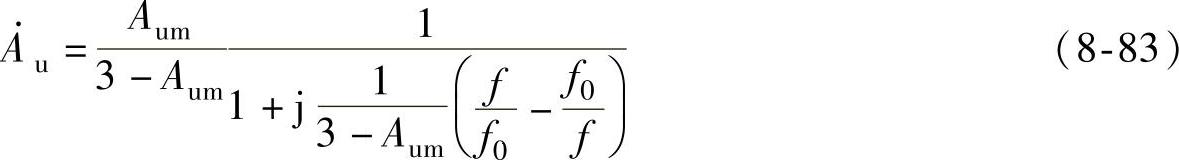
f=f₀时的电压放大倍数称为电路的通带放大倍数A_uP，即

式中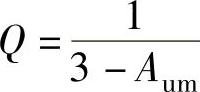，，它为电路的品质因数，将上式代入式（8-83）可得

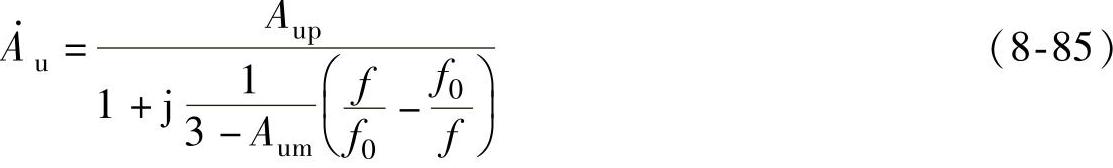
根据截止频率的定义式可得截止频率f_p所满足的方程为

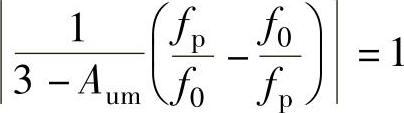
解方程，并取正数解可得

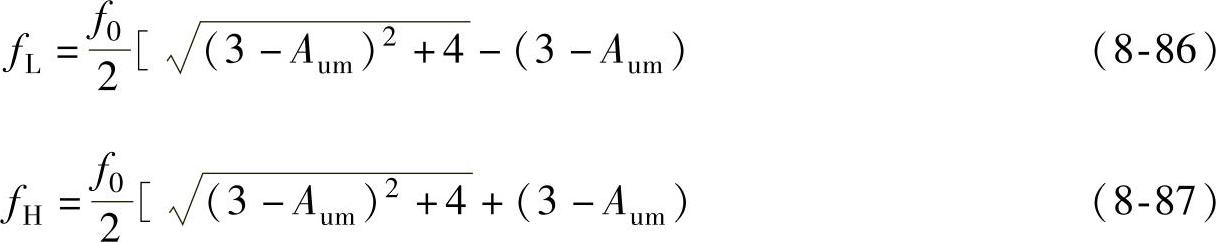
该电路的通带宽度为

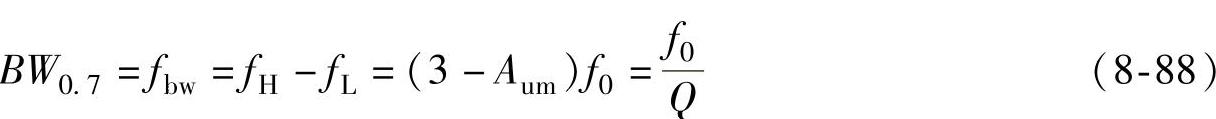
该电路的幅频特性为

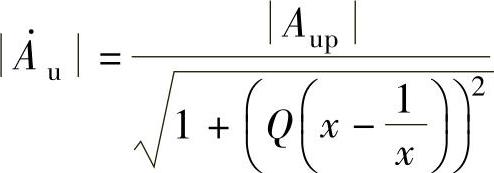
用MATLAB画带通滤波器幅频特性曲线的程序为

(https://www.xing528.com)

该程序运行的结果如图8-58所示。

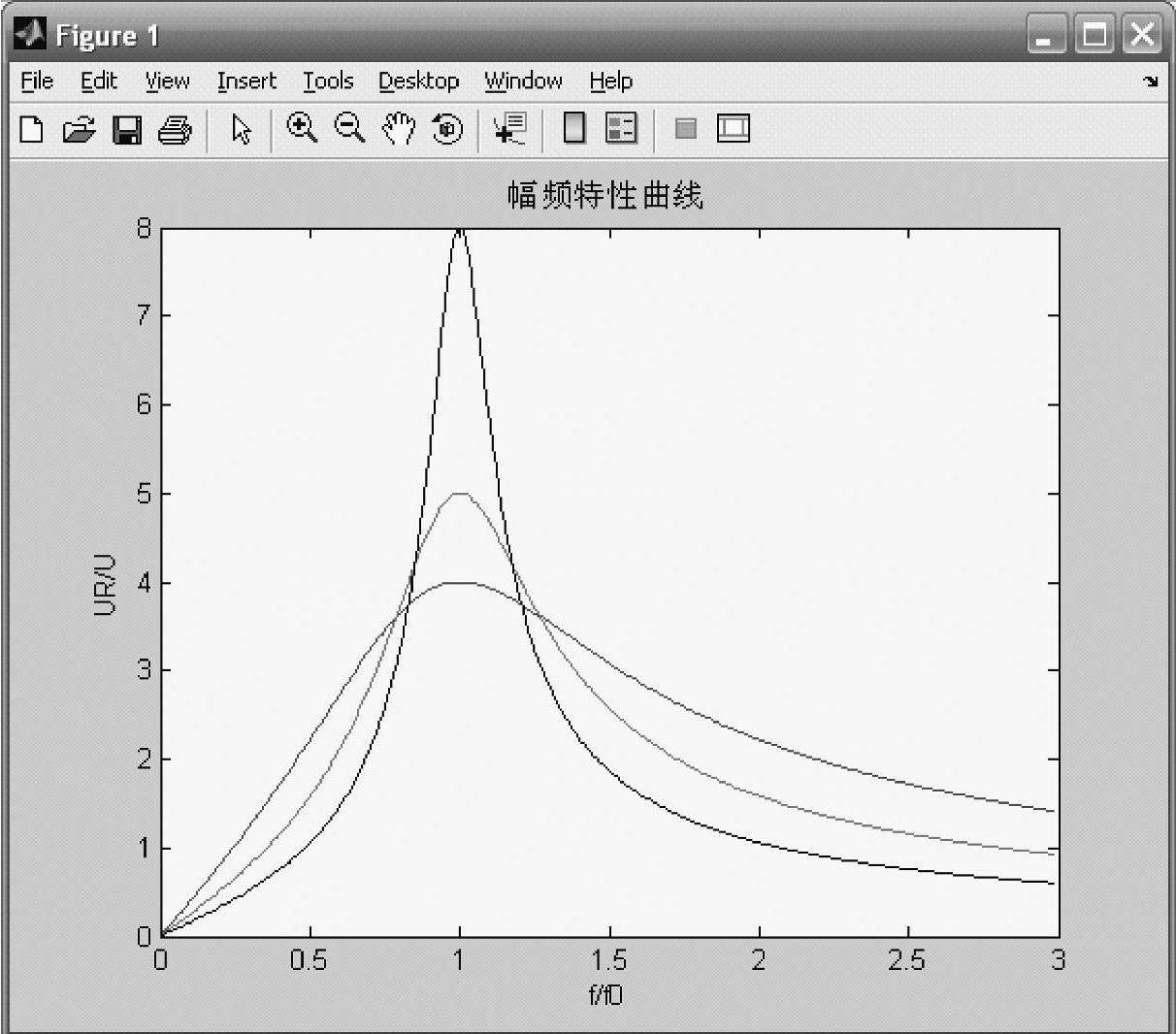
图8-58 不同Q值的带通滤波器幅频特性曲线

由图8-58可见，Q值越大，带宽越窄，选择性越好，通过调整电路的A_um，可以调节电路的Q值，改善电路的通频带宽度和选择性。

带通滤波器的信号输入端也可以是运放的反相输入端，组成反相输入的带通有源滤波器电路，如图8-59所示。图8-59说明，用RLC并联谐振电路替代反相比例运算放大器的反馈电阻R_f，即可组成反相输入的带通滤波器。

用仿真软件的波特图仪，可以测量图8-59所示电路的波特图如图8-60所示。

图8-60波特图仪屏幕上的第一个波形是图8-59所示电路波特图的幅频特性，第二个波形是图8-59所示电路波特图的相频特性。因为图8-60所显示的波特图与第6章介绍的选

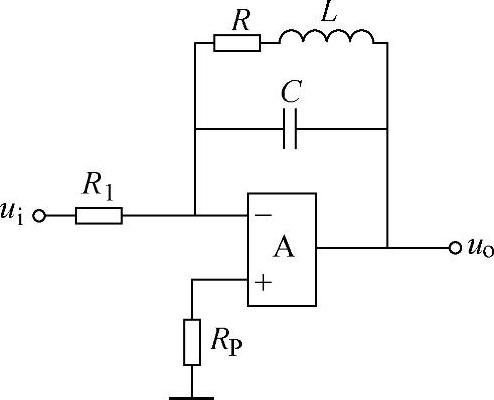
图8-59 反相输入的带通滤波器

频放大器的波特图相同，所以带通有源滤波器也可以称为选频放大器。

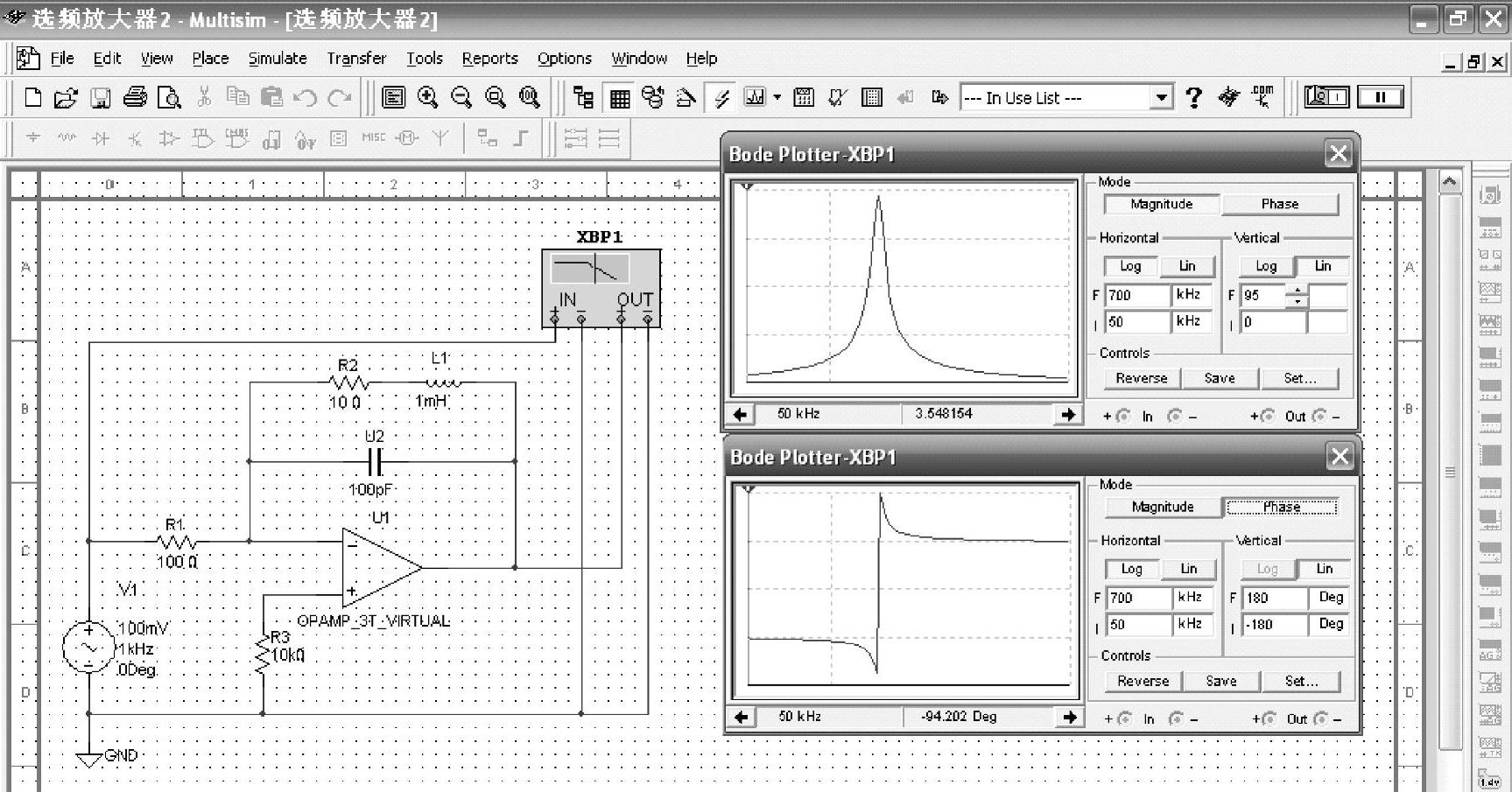
图8-60 选频放大器的波特图

根据反相比例运算放大器电压放大倍数的公式，可以推导出图8-59所示电路输出与输入信号的关系。由反相比例运算放大器电压放大倍数的公式可得

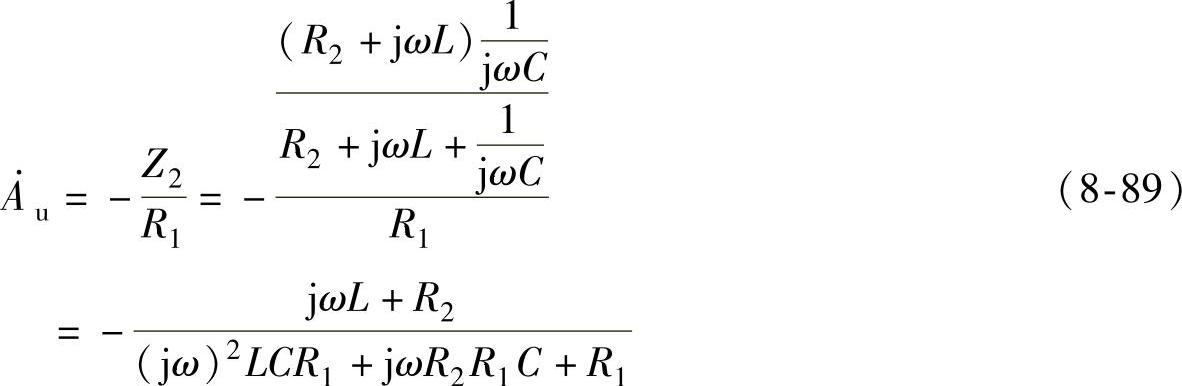
将图8-60电路中各器件的参数代入式（8-89）中，并用复变量s替代式（8-89）中的jω，就得到电压放大倍数的拉氏变换式。电压放大倍数的拉氏变换式在电路分析课程中称为象函数，式（8-89）的象函数为

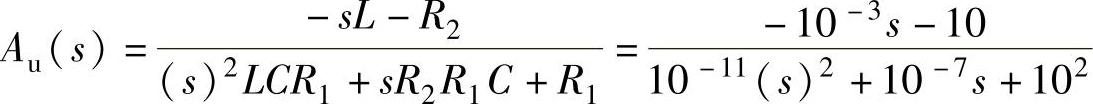
调用MATLAB画波特图的函数可以画出图8-59所示电路的波特图，画波特图的程序为

该程序运行的结果如图8-61所示。

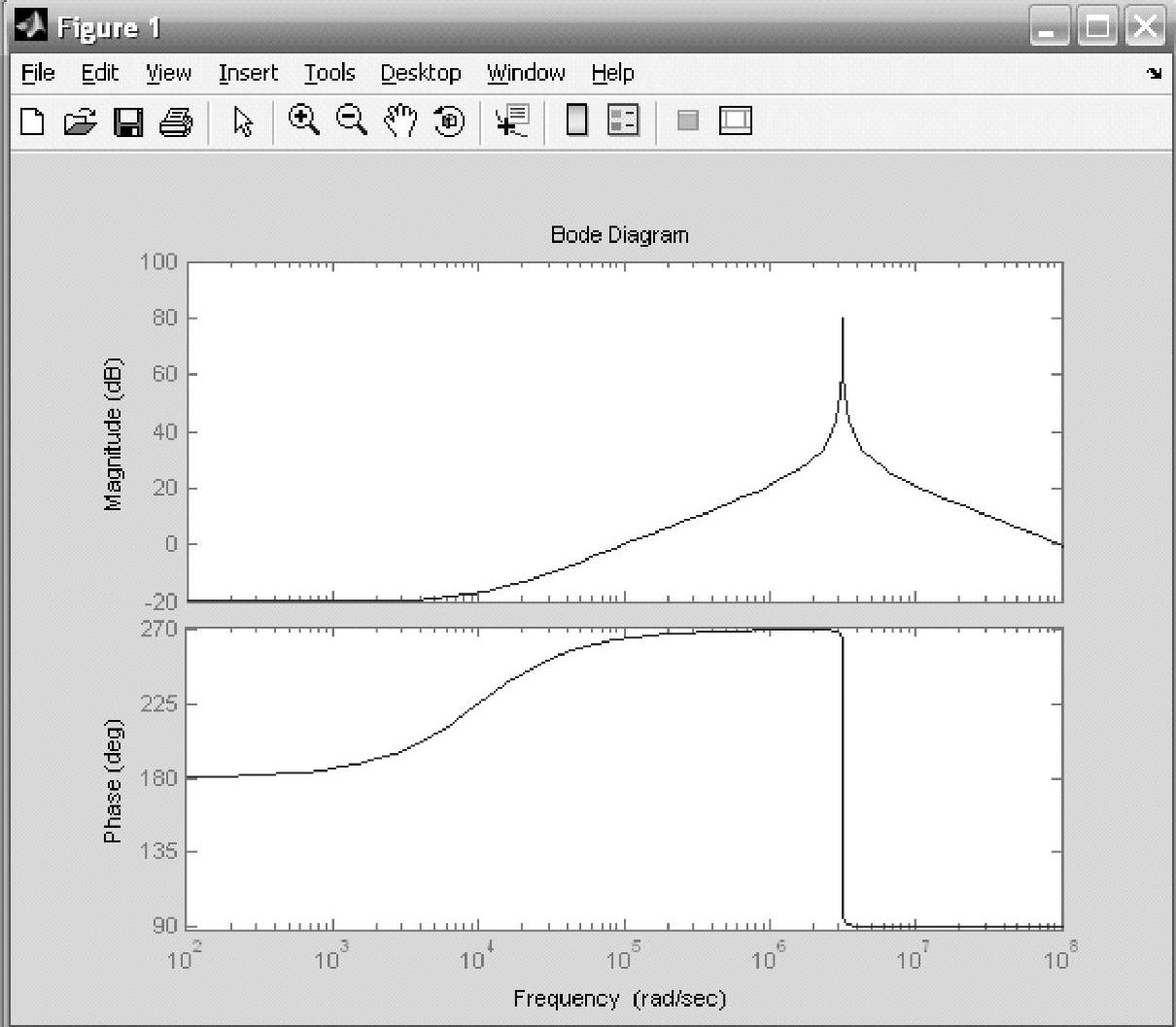
图8-61 图8-59所示的带通滤波器的波特图

图8-61的幅频特性与图8-60波特图仪上的图形相同，说明图8-59所示的电路是选频放大器。图8-61的相频特性曲线与图8-60波特图仪上的相频特性曲线的差别是由于纵轴的标度不同引起的，用三角函数的诱导公式改变标度后两张相频特性曲线将相同。

4.带阻滤波器

允许某一频段信号通过的电路称为带通滤波器，不允许某一频段信号通过的滤波器称为带阻滤波器，组成带阻滤波器的电路如图8-62所示。

图8-62说明，将低通滤波器和高通滤波器相并联后与运算放大器串联即可以组成带阻滤波器。

根据节点电位法和“虚短”、“虚断”的概念可得

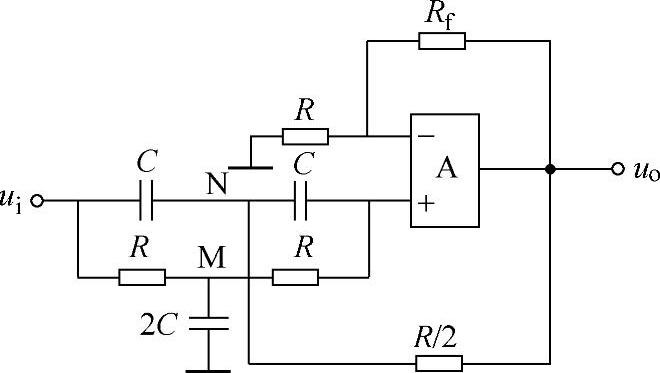
图8-62 带阻滤波器

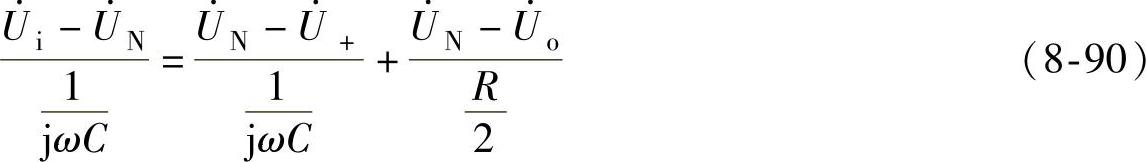
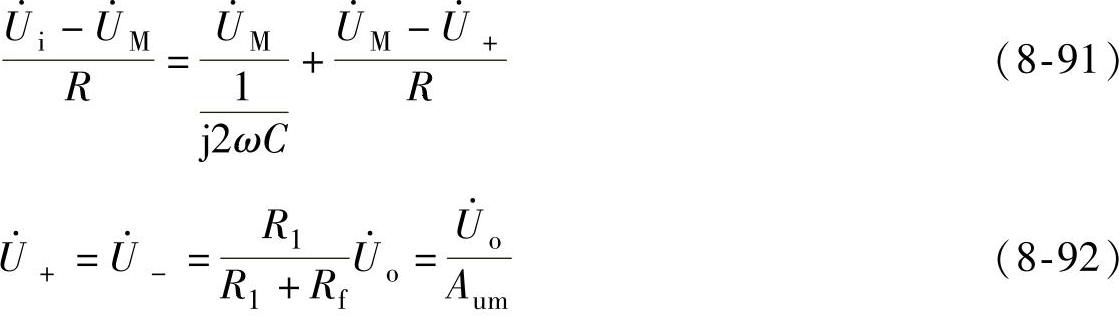
联立求解得

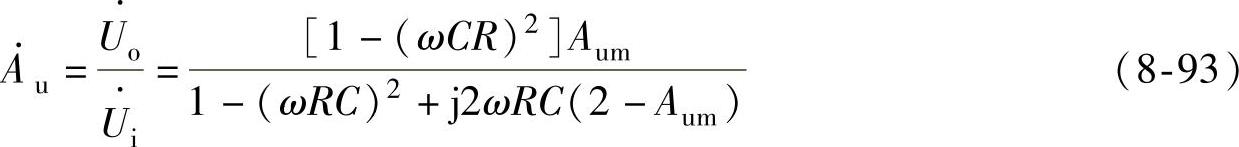
将带阻滤波器中心频率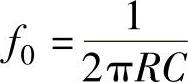的关系代入上式可得

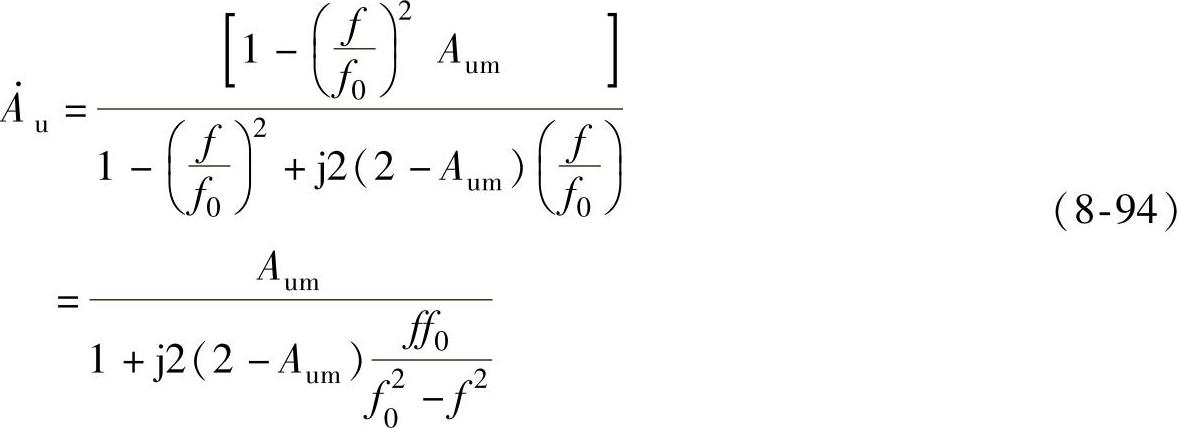
通带截止频率f_P所满足的方程为

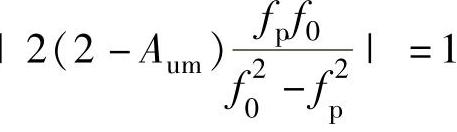
解方程，并取正数解可得

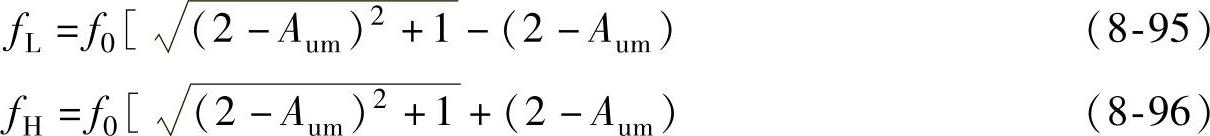
该电路的阻带宽度为

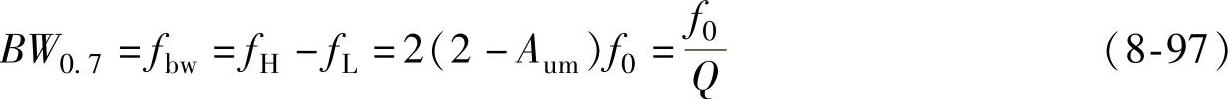
式中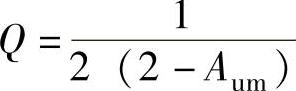，，它为电路的品质因数。在Multisim上得到的波特图如图8-63所示。

图8-63中的波特图清晰地显示出图8-62所示的电路不允许某些频段的信号通过，是带阻滤波器。

5.全通滤波器

（1）电路的组成

允许所有频率信号通过的电路称为全通滤波器，全通滤波器电路的组成如图8-64所示。

（2）电压放大倍数

根据“虚短”和“虚断”的概念可得

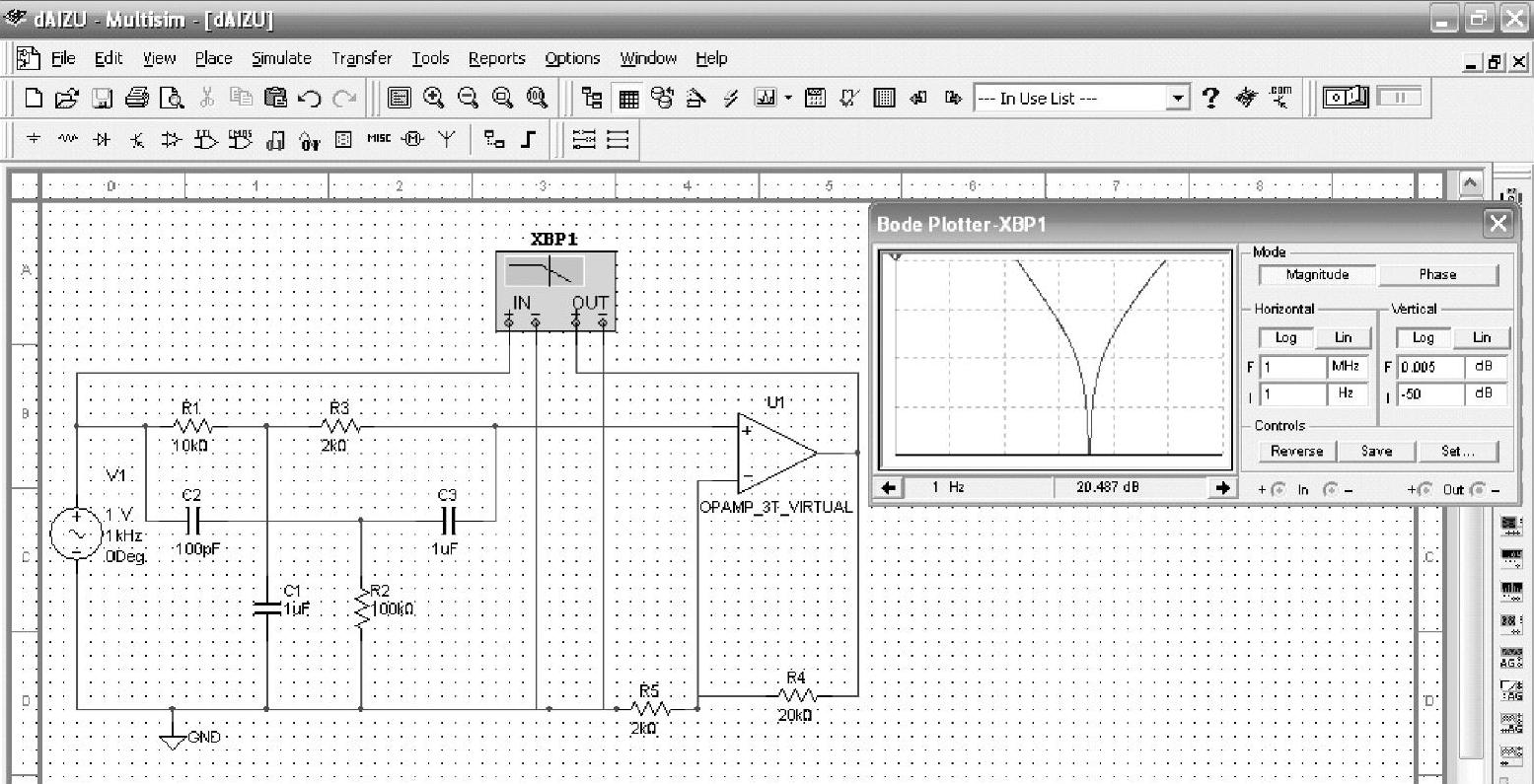
图8-63 带阻滤波器的幅频特性曲线

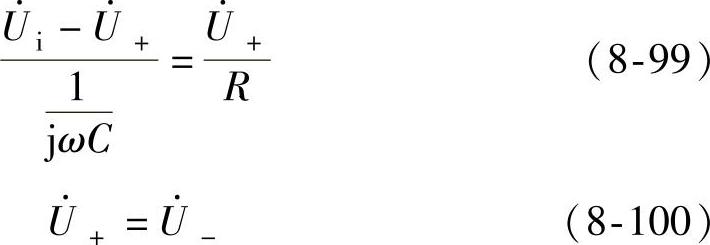
在R₁=R_f=R的条件下联立求解得

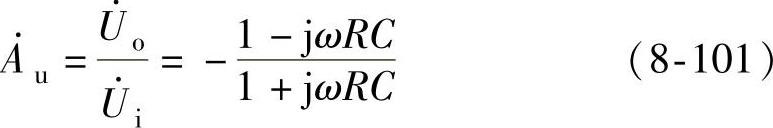
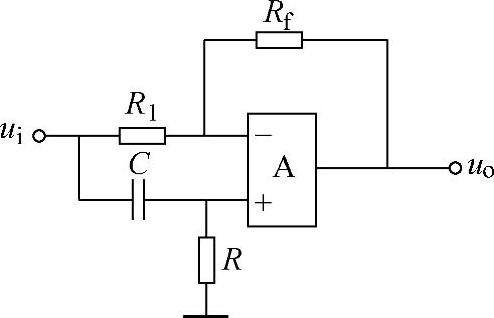
图8-64 全通滤波器

该电路的幅频特性为

式（8-102）说明该电路的幅频特性为常数，与频率无关，显示出全通滤波器的特征。全通滤波器电路的电压放大倍数的象函数为

【例8-9】 列出求解如图8-65所示电路的输出信号u_o1、u_o2和u_o3与输入信号u_i之间关系的矩阵。

解 根据节点电位法、“虚短”、“虚断”和“虚地”的概念可得

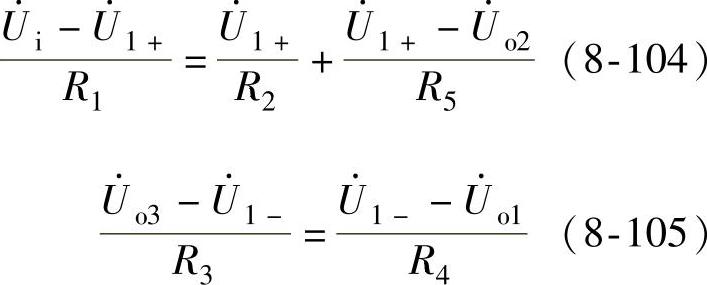
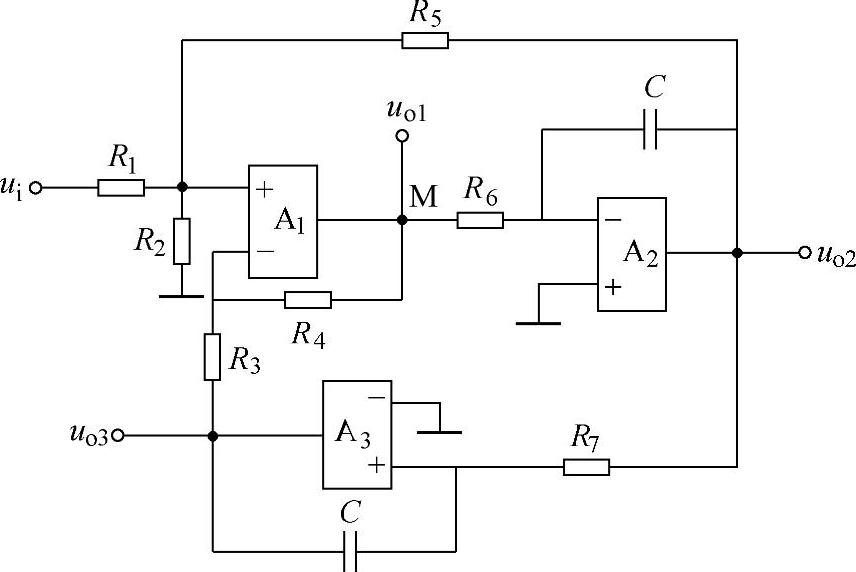
图8-65 例8-9图

联立式（8-104），式（8-105）和式（8-108）可得

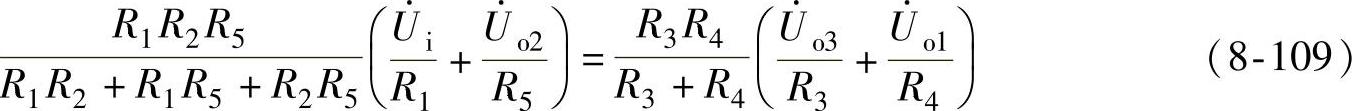
利用R_1P=R_1N的条件可得

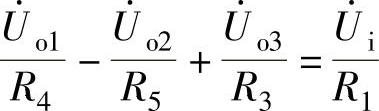
整理可得矩阵为

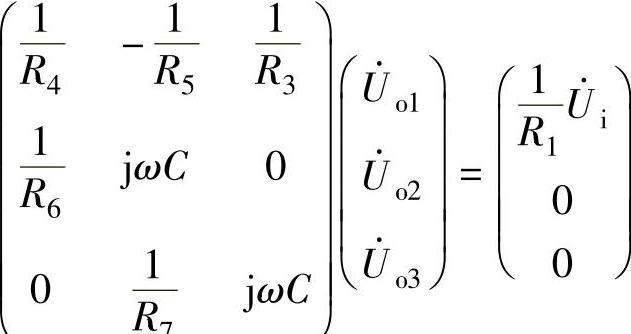
用MATLAB可求解各输出信号与输入信号之间的关系，根据这些关系可得不同的输出端所具有的滤波特性。