比例运算电路设计技巧

1.反相比例运算电路

（1）电路的组成

反相比例运算电路的组成如图8-12所示。在图8-12所示的电路中，输入电压u_i通过电阻R₁加在运放的反相输入端。R_f是沟通输出和输入的通道，是电路的反馈网络。

因该网络的两个端子分别与输出和输入端子接在一起，根据反馈组态的判别方法，可得该电路的反馈组态是：电压并联负反馈。

同相输入端所接的电阻R_P称为电路的平衡电阻，该电阻等于从运放的同相输入端往外看除源以后的等效电阻，为了保证运放电路工作在平衡的状态下，R_P的值应等于从运放的反相输入端往外看除源以后的等效电阻R_N，即

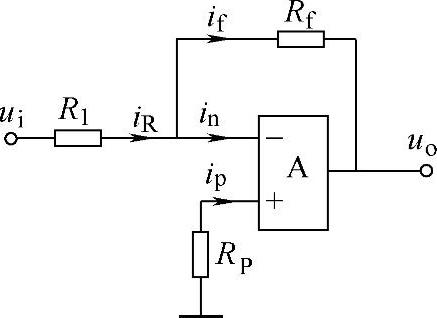
图8-12 反相比例运算电路

R_P=R_N （8-10）

式（8-10）是选择平衡电阻的基本关系式，对任何形式的运放电路均适用，但不同形式的运算放大器R_P和R_N的组态不相同，在本电路中R_N=R₁∕∕R_f=R_P。

（2）电压放大倍数

由上面的分析可知，反相比例运算放大器是属于电压并联负反馈放大器，根据第7章的知识可知，电压并联负反馈放大器的电压放大倍数是指电路的闭环源电压放大倍数，即A_usf。今后为了叙述的方便，将其简称为电压放大倍数，并用符号A_u来表示。

因为反相比例运算电路带有负反馈网络，所以集成运放工作在线性工作区。利用“虚断”和“虚短”的概念可以分析输出电压和输入电压的关系。根据“虚断”的概念可得

i_P=i_N=0 （8-11）

将“虚断”的关系代入KCL可得

i_R=i_f （8-12）

根据“虚短”的概念可得

u_-=u₊=0 （8-13）

式（8-13）说明，运放的反相输入端没有接地，却因同相输入端接地，使反相输入端也具有与“地”相同的电位，反相输入端的这种状态称为“虚地”。

注意：“虚地”和接地是不同的两个概念，“虚地”的特征是电位与地相同，但不接地，它是“虚短”在同相输入端的电位为零时的特例。利用“虚地”的概念可得

u_i=i_RR₁ （8-14）

u_o=-i_fR_f （8-15）

所以电压放大倍数A_u为

式（8-16）说明，输出电压和输入电压的大小成比例关系，且相位相反（式中的负号说明输出电压和输入电压相位相反），这也是反相比例运算放大器名称的由来。

反相比例运算放大器因引入电压负反馈，且反馈深度1+AF=∞，所以该电路的输出电阻r_o为

r_o=0 （8-17）

式（8-17）说明，反相比例运算放大器带负载的能力很大，带负载和不带负载时的运算关系保持不变。

根据“虚地”的概念可得反相比例运算电路的输入电阻r_i为

r_i=R₁ （8-18）

式（8-18）说明，虽然理想运放的输入电阻为无穷大，由于引入并联负反馈后，电路的输入电阻减少了，变成R₁，要提高反相比例运算放大器的输入电阻，需加大电阻R₁的值。R₁的值越大，R_f的值也必须加大，电路的噪声也将加大，稳定性变差。将图8-12电路中的电阻R_f改成T形网络就可以解决由于R_f电阻太大而影响电路性能的问题。

2.T形网络反相比例运算电路

（1）电路的组成

T形网络反相比例运算电路的组成如图8-13所示。由图8-13可见，反相比例运算放大器电路中的电阻R_f被R₂、R₃和R₄电阻所组成的T形网络替代，所以该电路称为T形网络反相比例运算放大器。

（2）电压放大倍数

利用“虚断”、“虚地”的概念和节点电位法可求得该电路输出电压和输入电压的关系，根据“虚断”和“虚地”的概念可得

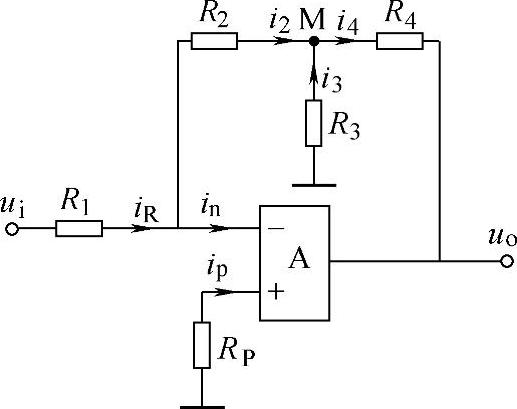
图8-13 T形网络反相比例运算电路

根据节点电位法可得

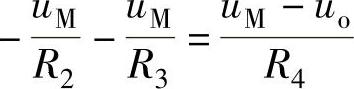
将式（8-19）的结果代入可得

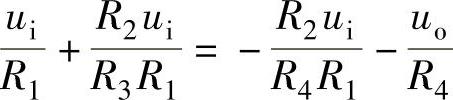
移项整理可得

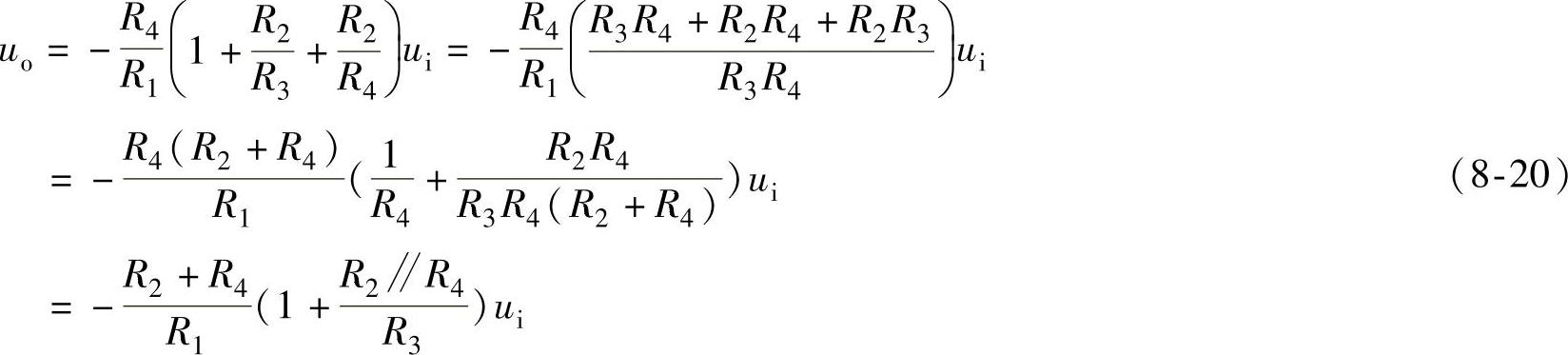
式（8-20）表明，当R₃=∞时，式（8-20）与式（8-16）的结论相同。T形网络电路的输入电阻也是R₁，但引入R₃以后，使电路的反馈系数减小，电压放大倍数增加，用较小的反馈电阻，可以得到较大的电压放大倍数。同时也解决了由于R_f电阻太大而影响电路性能的问题。

T形网络反向比例运算电路中的平衡电阻为

R_P=R_N=R₁∥（R₂+R₃∥R₄）

利用第7章介绍的深度负反馈放大器的分析方法也可得到式（8-16）的结论。分析的方法是：设电路各电流的参考方向如图8-13所示，根据反馈网络单向化处理的原则和反馈系数的定义式可得

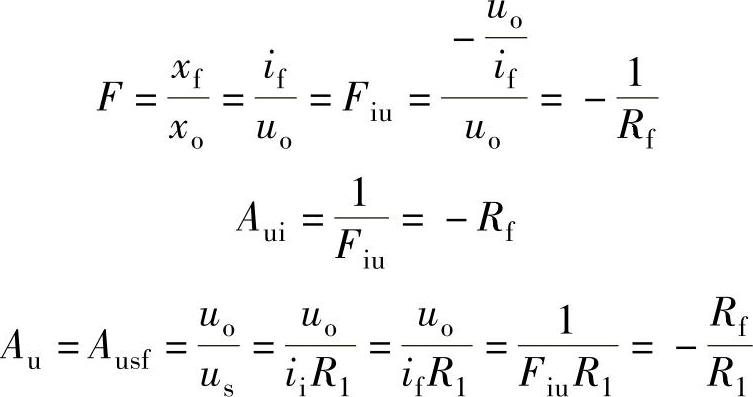
与式（8-16）的结论相同。反相比例运算放大器电压放大倍数仿真测试的结果如图8-14所示。

图8-14 反相比例运算放大器电压放大倍数计算公式仿真测试的结果

图8-14左边的电路R₁=10kΩ，R_f=100kΩ，A_u=-10；右边的电路R₁=R₃=10kΩ，R₂=R₄=20kΩ，A_u=-8。在图8-14中示波器的屏幕上，第一个波形是电压幅度为10mV的输入信号；第二个波形是相位与输入信号相反，幅度为100mV的输出信号，证明左边的电路A_u=-10；第三个波形是相位与输入信号相反，幅度为80mV的输出信号，证明右边的电路A_u=-8。

3.同相比例运算电路

（1）电路的组成(www.xing528.com)

同相比例运算电路的组成如图8-15所示。在图8-15所示的电路中，输入电压u_i通过电阻R_P加在运放的同相输入端。R_f是沟通输出和输入的通道，是电路的反馈网络。

因该网络的一个端子与输出端子接在一起，另一个端子没有与输入端子接在一起，根据反馈组态的判别方法，可得该电路的反馈组态是电压串联负反馈。

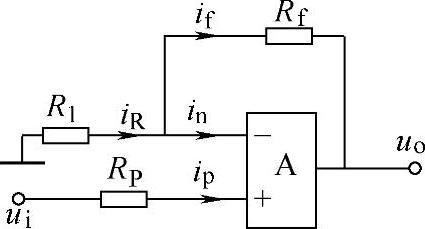
图8-15 同相比例运算电路

（2）电压放大倍数

利用“虚断”和“虚短”的概念可分析同相比例运算电路输出电压和输入电压的关系。根据“虚断”的概念可得

i_P=i_N=0 （8-21）

根据“虚短”的概念可得

根据电压放大倍数的表达式可得

式（8-23）说明输出电压和输入电压的大小成比例关系，且相位相同，这也是同相比例运算放大器名称的由来。

为了电路的对称性和平衡电阻调试的方便，同相比例运算放大器通常还接成如图8-16所示的形式。因该电路的u+为

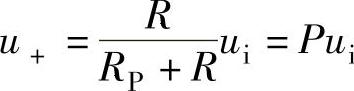
式中，P为串联电路的分压比，所以该电路的电压放大倍数为

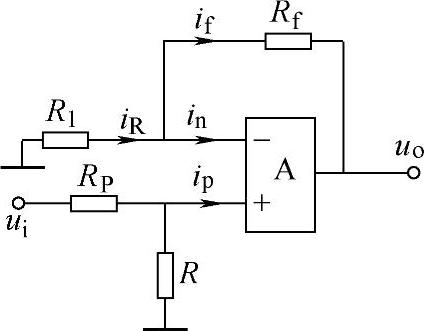
图8-16 同相比例运算电路

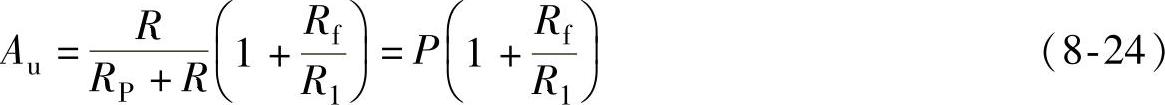
式（8-24）说明，两种形式的同相比例运算电路，电压放大倍数的公式仅相差一个分压比P。

4.电压跟随器

在图8-15所示的电路中，若令R_f=0，则电路变成如图8-17a所示的形式，图8-17b为R₁=∞的特例。

根据式（8-23）可得

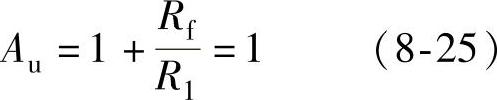
式（8-25）说明图8-17所示电路的电压放大倍数等于1，输出电压随着输入电压的变化而变化，具有这种特征的电路称为电压跟随器。

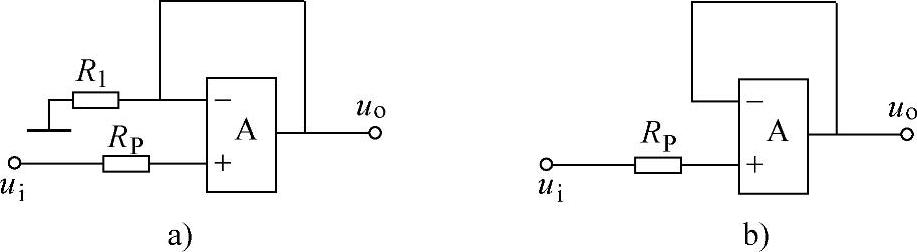
图8-17 电压跟随器

【例8-1】 图8-18所示的同相比例运算电路，已知A_v=10，且R₁=R₂。

（1）求R₃和R₄与R₁的关系。

（2）当输入电压u_i=2mV时，R₁的接地点因虚焊而开路，求输出电压u_o的值。

解 根据式（8-24）和式（8-10）可得

R_P=R₂∥R₄=R_N=R₁∥R₃（8-27）

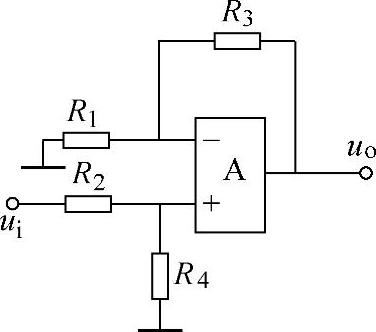
图8-18 例8-1图

已知R₁=R₂，根据式（8-27）可得R₃=R₄。将结果代入式（8-26）可得

R₃=R₄=10R₁

当R₁的接地点断开时，相当于式（8-26）中的R₁=∞，电路变成电压跟随器。根据电压跟随器输出电压与输入电压相等的特征可得

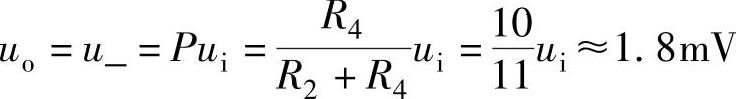
上述解的过程仿真实验的结果如图8-19所示。

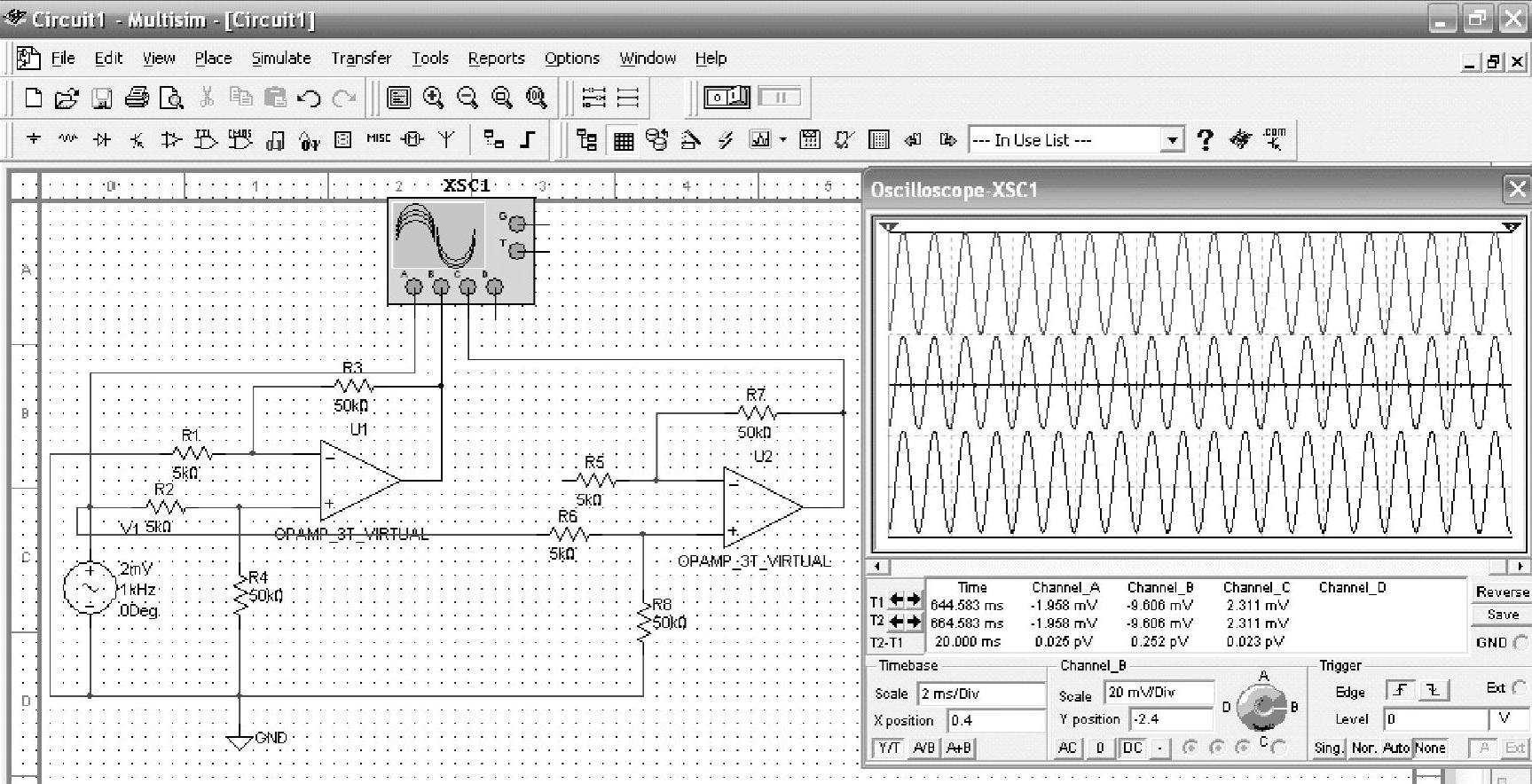
图8-19 例8-1解仿真实验的结果

图8-19左边所示的电路是解（1）的仿真电路，右边的电路是解（2）的仿真电路。示波器屏幕上的第一个波形是输入信号的波形，第二个波形是右边电路输出信号的波形，第三个波形是左边电路输出信号的波形，根据示波器满刻度的数值可验证解的正确性。

【例8-2】 如图8-20所示的比例运算电路，已知A_u=-33，且R₁=10kΩ，R₂=R₄=100kΩ，求R₅和R₆的阻值。

解 该运算电路由两级运算电路组成，第一个运放A₁组成同相比例运算放大器，第二级A₂组成反相比例运算放大器，根据多级放大器电压放大倍数的公式可得

图8-20 例8-2图

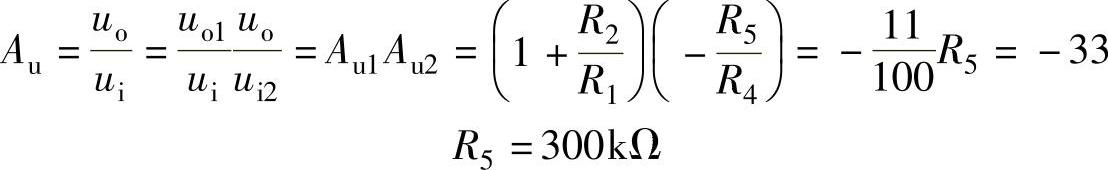
根据R_P=R_N的关系可得R₆的值为

R₆=R₄∥R₅=75kΩ

上述解的过程仿真实验的结果如图8-21所示。

图8-21 例8-2解仿真实验的结果

图8-21中示波器屏幕上的波形清晰地显示出，图8-21所示电路的输出信号与输入信号反相，且电压放大倍数为33。