晶体管高频等效模型简介及优化

晶体管低频等效模型，即晶体管的微变等效电路不考虑晶体管结电容的作用，将晶体管的输入端等效成一个电阻r_be，输出端等效成一个受控电流源βi_b。在高频电路中，晶体管结电容的效应不能忽略，晶体管内部有两个PN结，存在着两个结电容，考虑结电容效应后的晶体管等效电路模型称为晶体管高频等效模型，又称为混合π参数模型。晶体管混合π参数模型的电路如图6-65所示。

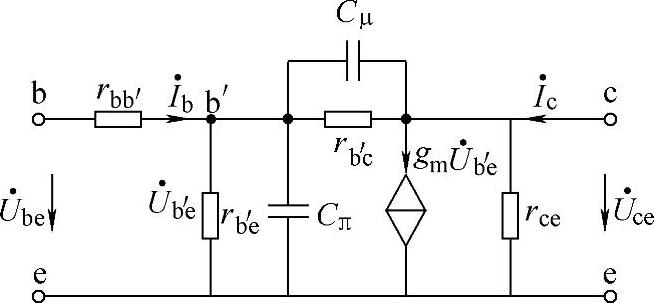
图6-65 混合π参数模型

由图6-65可见，在低频小信号微变等效电路的基础上，考虑发射结电容C_π和集电结电容C_μ的作用，就可得到晶体管混合π参数模型电路。图6-65中的r_bb′是晶体管基极的体电阻，r_b′e是发射结的结电阻，r_b′c是集电结的结电阻，r_ce是晶体管集电极和发射极之间的电阻。

在晶体管混合π参数模型中，因C_π和C_μ的存在，使i_b和i_c的大小和相角均与频率有关，即β是频率的函数。又因为i_b随C_π的变化而变化，所以不能用i_c=βi_b的关系来描述受控电流源与激励源的关系。在这种情况下，因输入端是RC混联电路，该电路的输出信号是u_b′e，所以要用i_c=g_mu_b′e的关系来描述受控电流源与激励源的关系，式中的g_m称为跨导，它是描述输入电压对输出电流控制作用大小的物理量，即

在低频的情况下，g_m的表达式可写成

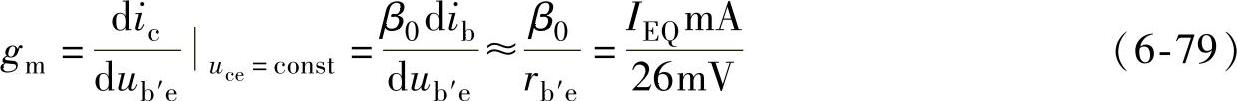
在图6-65所示的电路中，r_ce通常比与它并联的负载电阻R_L大很多，可忽略；r_b′c通常也比C_μ的容抗大很多，也可忽略。由此可得简化的混合π参数模型电路如图6-66a所示。

在图6-66a中，因C_μ跨接在输入和输出之间，给分析计算带来麻烦。为了解决这一问题，必须对C_μ进行单向化处理，单向化处理的办法是：将C_μ等效成一个并接在b′e间的电容C_μ′，和一个并接在ce间的电容C″_μ，如图6-66b所示。

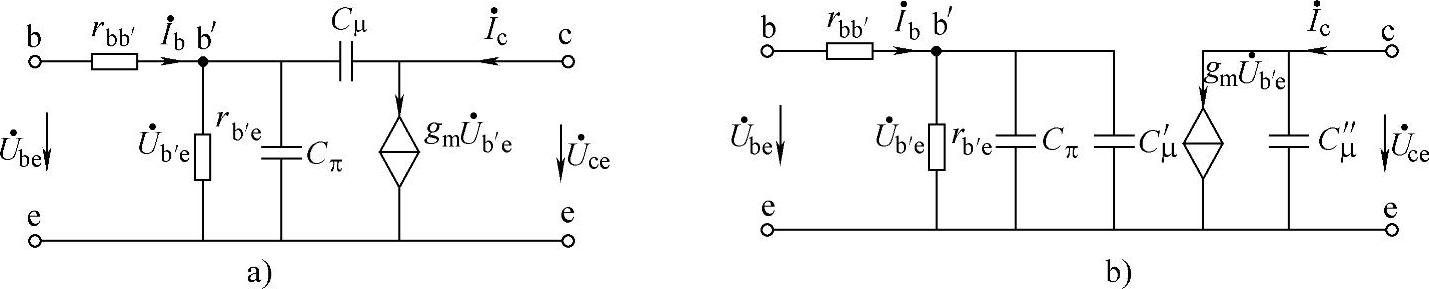
图6-66 简化的混合π参数模型

利用等效变换外特性相等的特点可确定等效电容C′_μ和C″_μ与原电容C_μ的关系。在图6-66a中流过电容C_μ的电流，应等于图6-66b中流过电容C_μ′的电流，即(www.xing528.com)

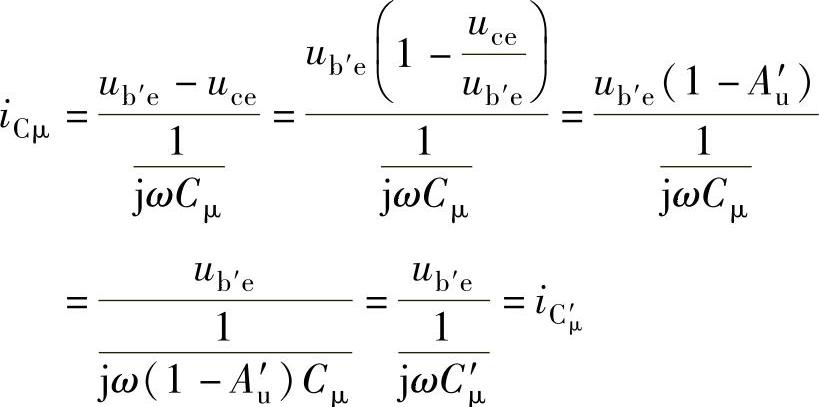
比较C_μ和C_μ′前的系数可得

C_μ′=（1-A_u′）C_μ （6-80）

式中

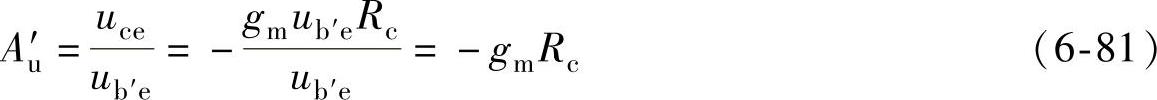
是电路处在中频时的电压放大倍数。根据图6-66b可得，并接在输入端b′e两端的总电容为

C_π′=C_π+C_μ′ （6-82）

同理可得C″_μ为

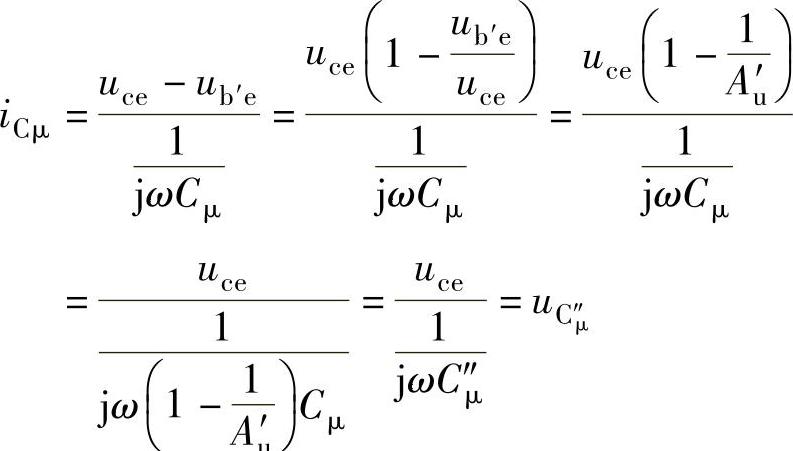
比较C_μ和C″_μ前的系数可得

由上式所确定的C″_μ通常很小可忽略，最后可得简化的混合π参数模型电路如图6-67所示。