二端口网络级联的原理与应用

在二端口网络的分析中，一个常见的问题是：给定二端口网络列参数方程和参数方程的转换。研究这一类问题的方法可以采用直流电路分析法的思路，将一个复杂的电路分解成几个简单电路的级联。二端口网络的级联有如图4-6所示的链联、串联和并联三种形式。

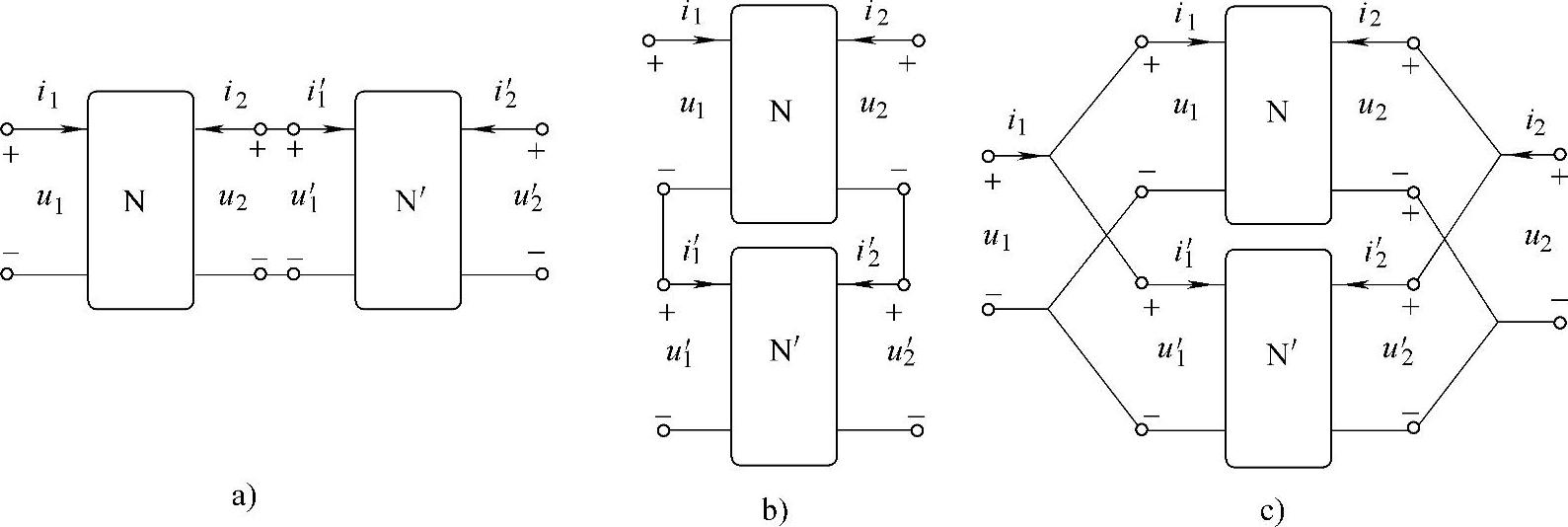
图4-6 二端口网络的级联

图4-6a是二端口网络的链联，图4-6b是二端口网络的串联，图4-6c是二端口网络的并联。

因为二端口网络链联的特点是第一级的输出等于第二级的输入，所以研究二端口网络链联的问题采用A参数方程比较方便。设第一级的A参数矩阵为A₁，第二级的A参数矩阵为A₂，二端口网络总的A参数矩阵为

A=A₁A₂ （4-31）

因为二端口网络串联的特点是阻抗相加，所以，研究二端口网络串联的问题采用Z参数方程比较方便。设两个相串联的Z参数矩阵分别为Z₁和Z₂，二端口网络相串联总的Z参数矩阵为

Z=Z₁+Z₂ （4-32）

因为二端口网络并联的特点是电导相加，所以，研究二端口网络并联的问题采用Y参数方程比较方便。设两个相并联的Y参数矩阵分别为Y₁和Y₂，二端口网络相并联总的Y参数矩阵为

Y=Y₁+Y₂ （4-33）

注意：上面的运算关系为矩阵的运算，利用线性代数的知识可以进行矩阵相乘和相加的运算。下面举几个求二端口网络参数方程的例子。

【例4-5】 用二端口网络级联的方法求图4-4所示电路的A参数方程。

解 图4-4a所示的二端口网络可以看成是例4-1所示的二端口网络的级联，级联的电路如图4-7a所示。

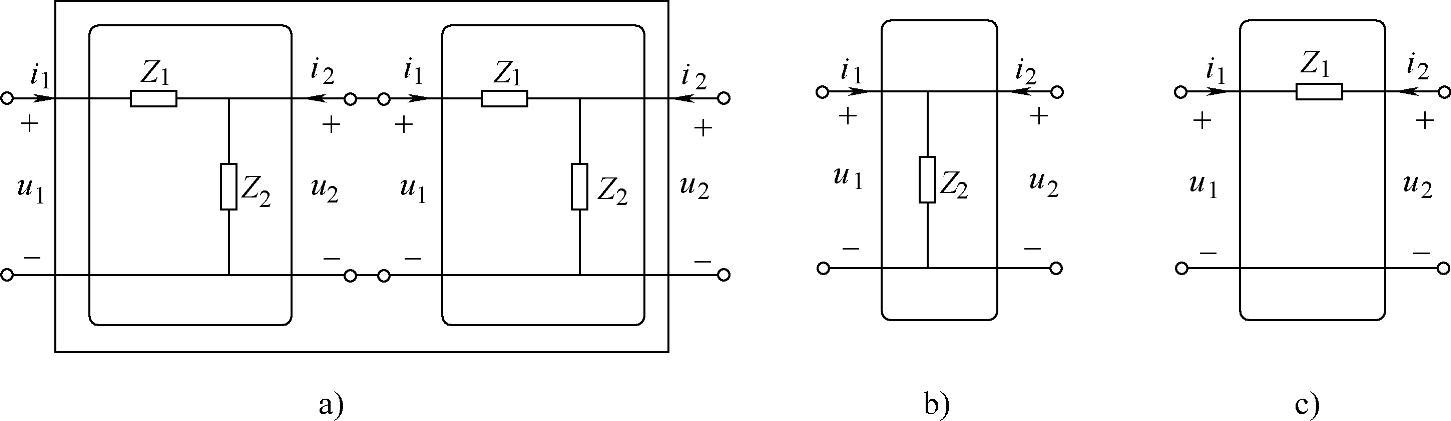
图4-7 例4-5解的电路

根据图4-7a可得，图4-4a所示的电路，可以看成第一个二端口网络Z参数的Z₁=0，Z₂=Z₃₁，等效的二端口网络如图4-7b所示，根据例4-1的结论可得

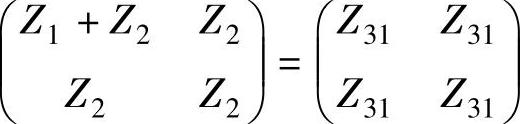
第二个二端口网络的Z参数为Z₁=Z₁₂，Z₂=Z₂₃。(www.xing528.com)

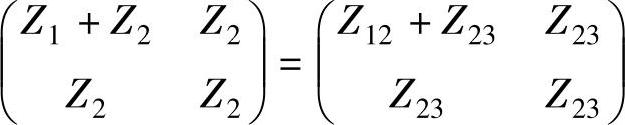
根据Z参数和A参数转换的公式可得两个二端口网络的A参数分别为

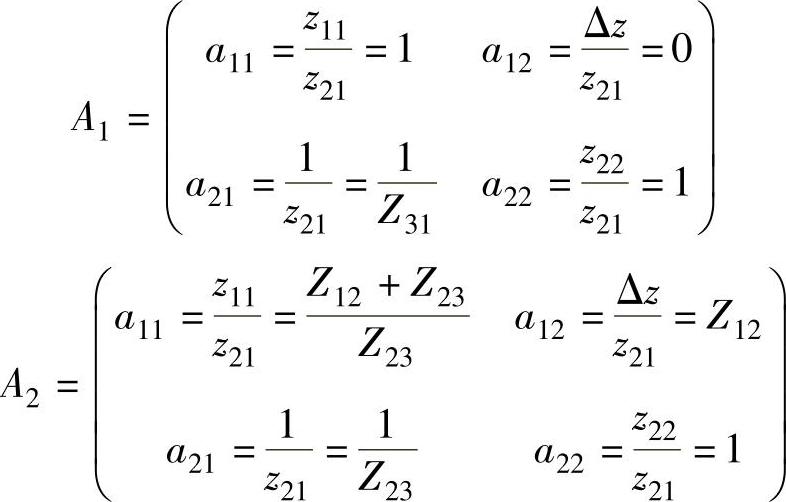
两个二端口网络级联的结果为

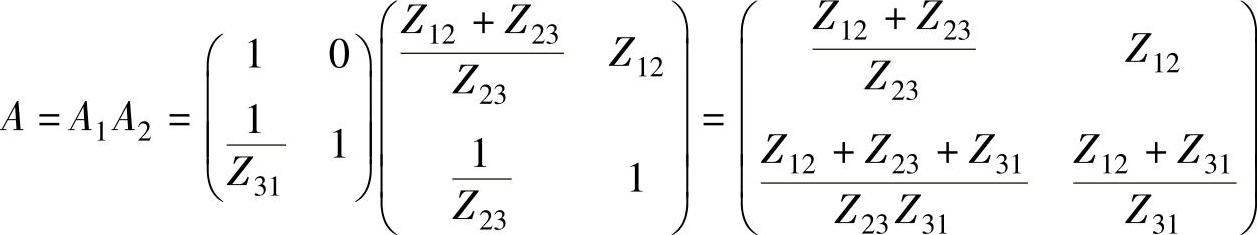
根据图4-7a可得，图4-4b所示的电路，可以看成第一个二端口网络Z参数的Z₁=Z₁，Z₂=Z₃，根据例4-1的结论可得

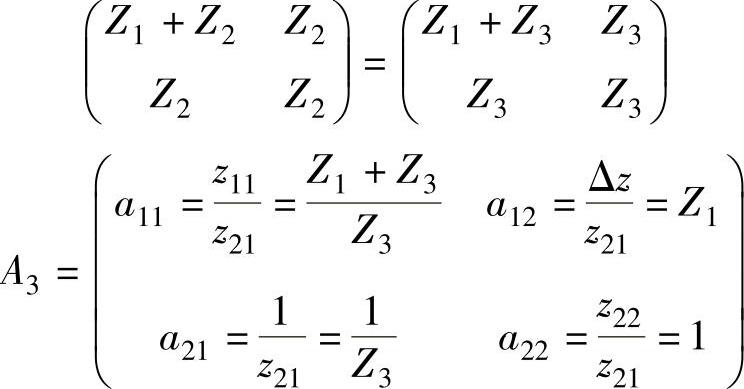
第二个二端口网络的Z参数为Z₁=Z₂，Z₂=∞，等效电路如图4-7c所示的二端口网络，该二端口网络的Z参数为∞，根据例4-1的结论可得

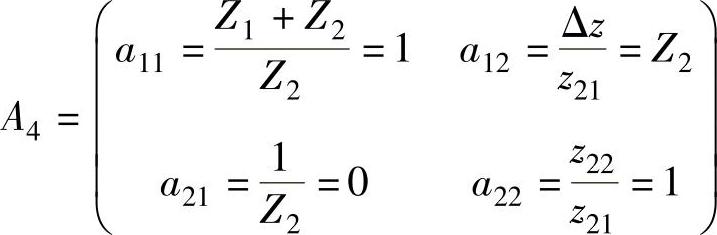
两个二端口网络级联的结果为

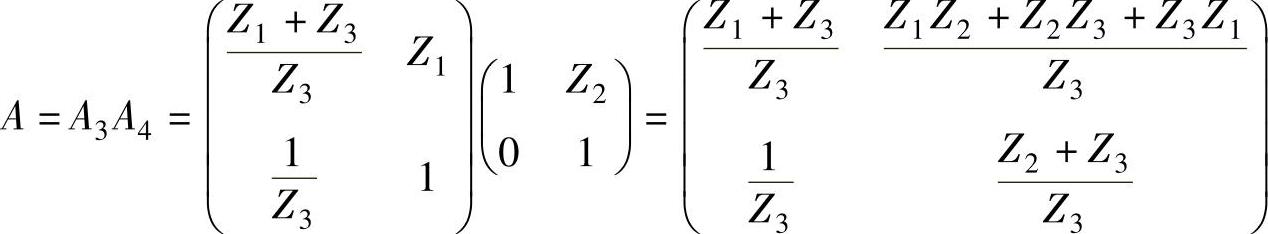
根据A参数相等的条件可得与例4-3相等的结论，用MATLAB计算的源程序为

该程序运行的结果为