二端口网络参数方程的转换方法

二端口网络的外特性当自变量和因变量的组合不同时，共有6个不同的方程组。但是同一个二端口网络的6个方程组不是独立的，只要知道其中的一个方程组就可以推出其他的5个，下面来讨论方程组转换的方法。

已知二端口网络的Z参数方程为

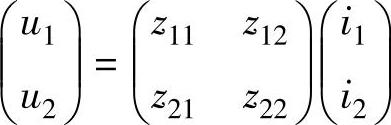
要将Z参数方程转换成A参数方程，必须先求解Z参数方程，根据线性代数的克拉默法则可得

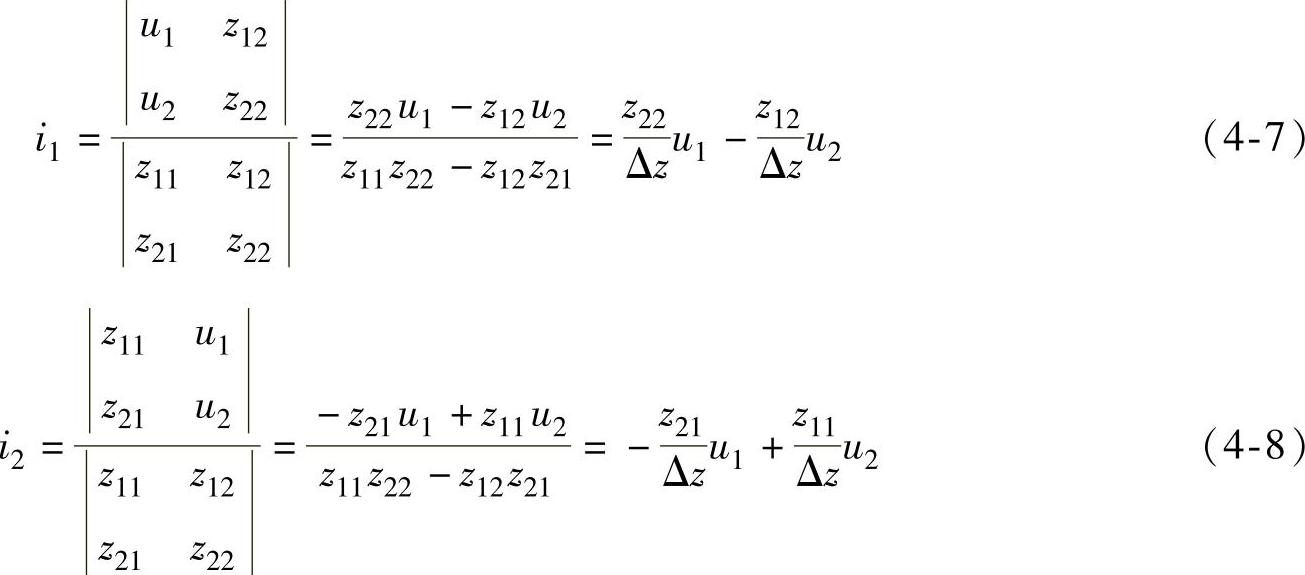
根据式（4-8）可得

将式（4-9）代入式（4-7）可得

将式（4-9）和式（4-10）写成矩阵可得

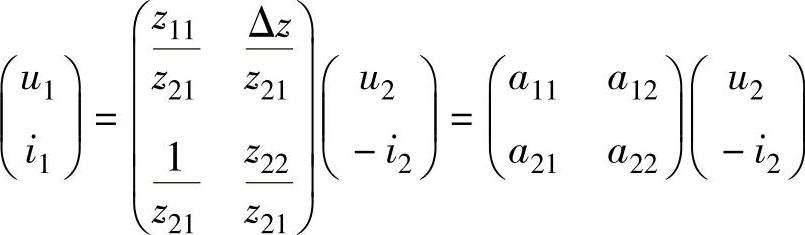
比较系数可得Z参数和A参数转换的公式为

用相同的方法也可以推出A参数和Z参数转换的公式为

移项整理式（4-10）可得

将式（4-13）代入式（4-9）可得

将式（4-13）和式（4-14）写成H参数方程的形式，比较系数可得Z参数和H参数转换的公式为

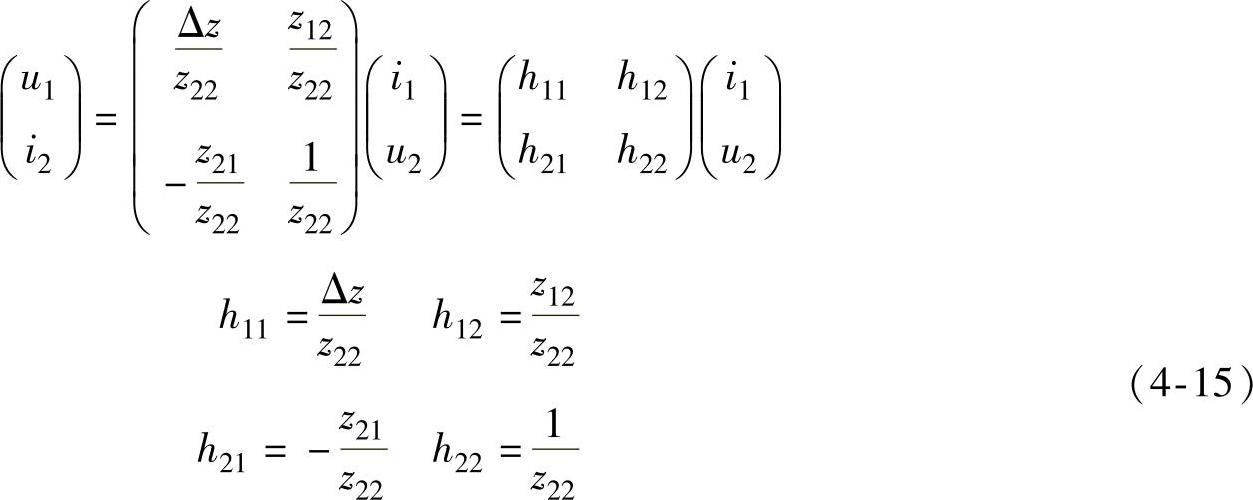
移项整理式（4-14）可得

将式（4-16）代入式（4-13）可得

将式（4-16）和式（4-17）写成Y参数方程的形式，比较系数可得Z参数和Y参数转换的公式为

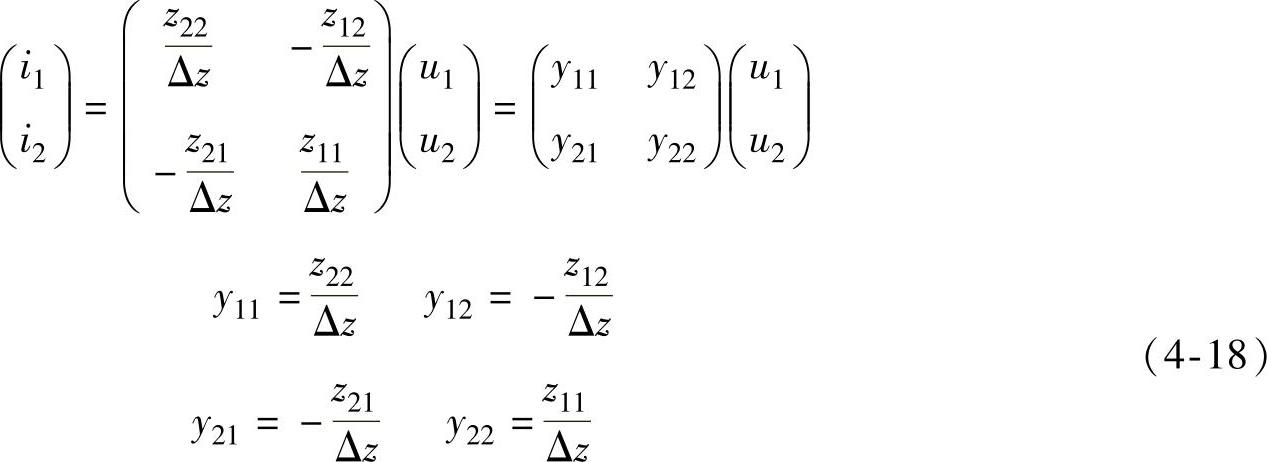
常用的变换公式就是这几个，用相同的方法也可以推出其他的变换公式留做习题请读者自己完成。

【例4-1】 已知图4-2所示电路的Z参数方程为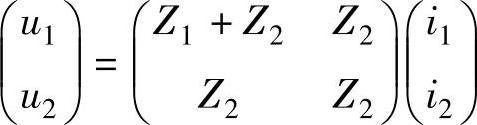，利用参数变换的公式求出该电路的A参数方程和H参数方程。

解 根据Z参数和A参数转换的公式可得

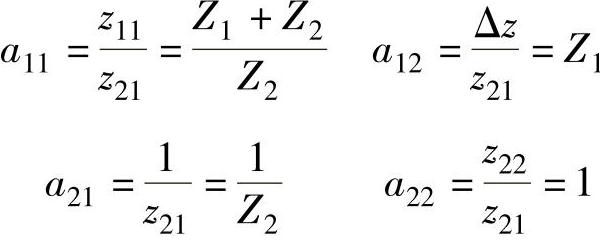
根据Z参数和H参数转换的公式可得

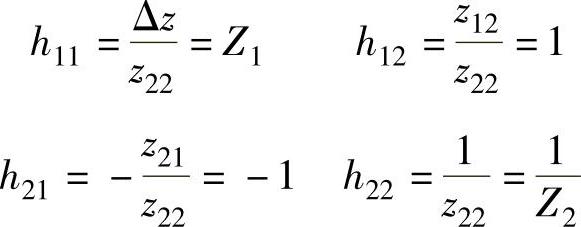
上述计算的过程可以用MATLAB编写的程序来完成，求解计算的程序为

与理论计算的结果相吻合。

【例4-2】 求图4-3所示电路的Z参数方程，并利用MATLAB求出该电路的A参数方程和H参数方程。

解 根据Z参数的定义可得图4-3所示二端口网络的Z参数方程为

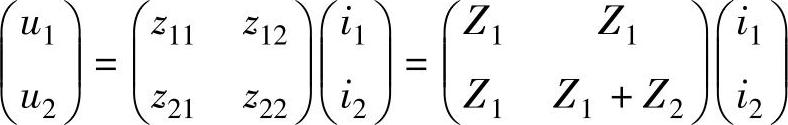
根据Z参数转A参数和Z参数转H参数的公式，用MAT-LAB编写的计算公式为

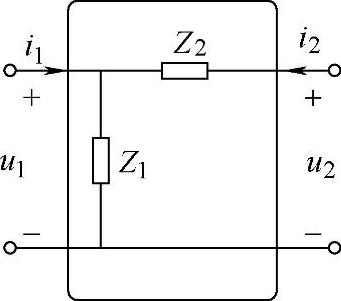
图4-3 例4-2图

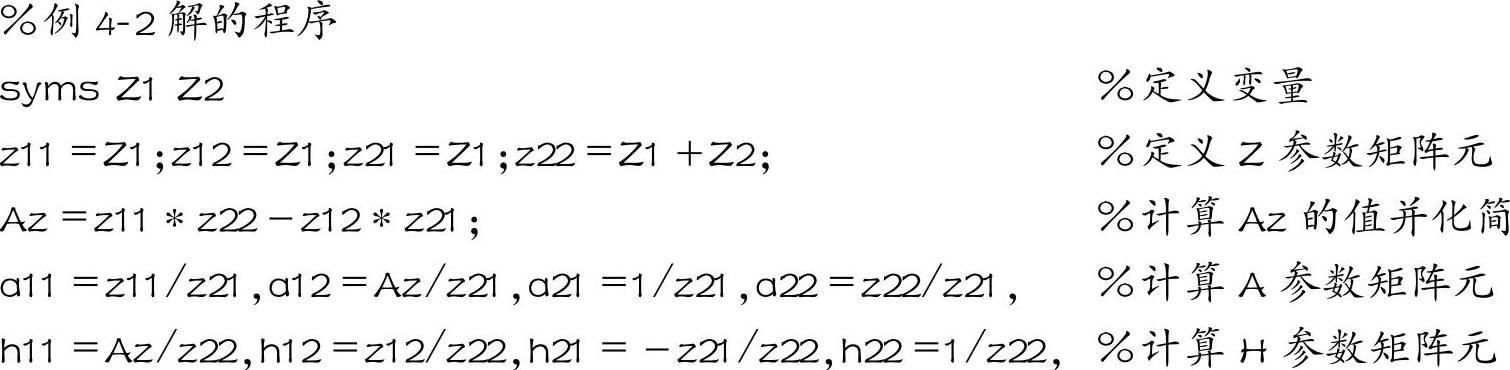
该程序运行的结果为

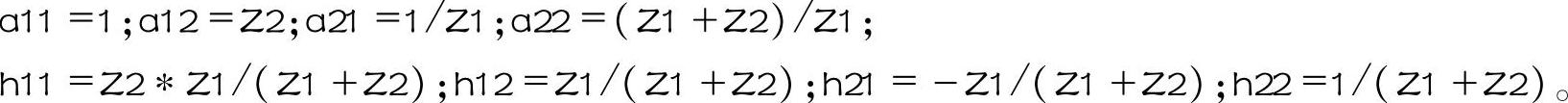
整理可得图4-3所示的二端口网络的A参数方程和H参数方程为

【例4-3】 求图4-4所示的二端口网络等效变换的关系。(www.xing528.com)

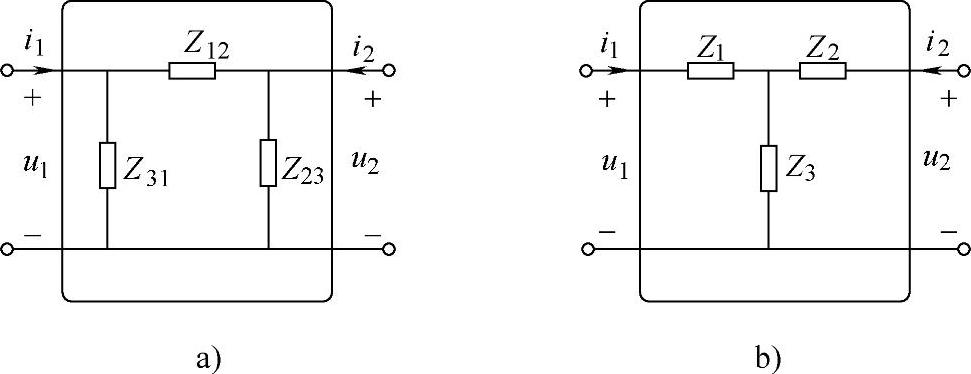
图4-4 例4-3的网络图

解 图4-4a所示的二端口网络称为л（Δ）形网络，图4-4b所示的二端口网络称为T（Y）形网络，用二端口网络的理论可以求出л形网络和T形网络等效变换的关系。根据叠加定理可得图4-4a所示电路的Z参数方程为

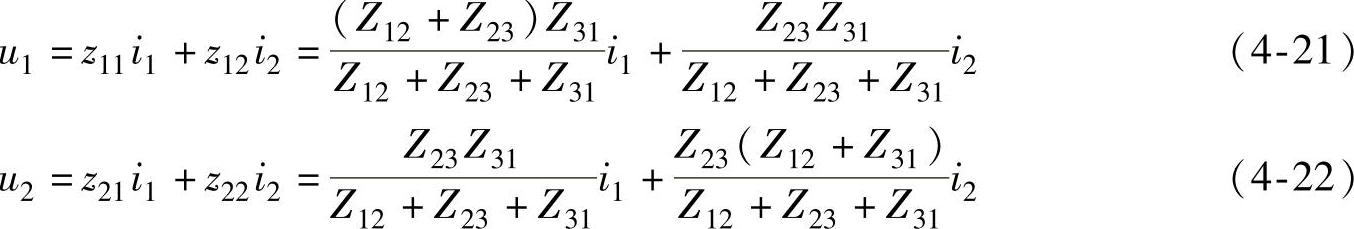
根据叠加定理可得图4-4b所示电路的Z参数方程为

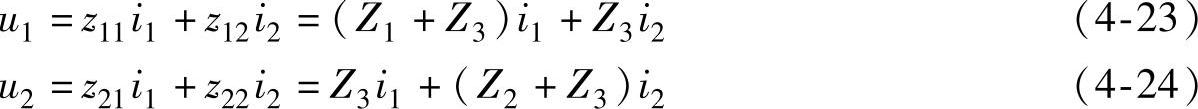
两个电路等效变换要满足的条件是Z参数相等，根据Z参数相等的条件可得

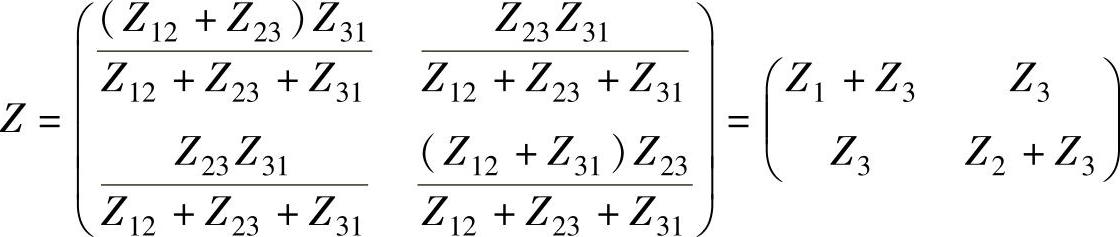
比较系数可得

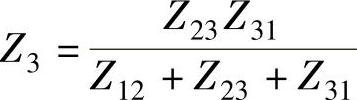
根据Z参数转A参数的公式可得

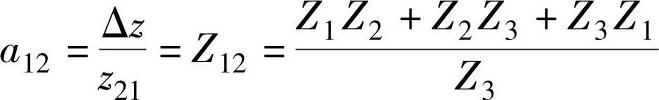
利用MATLAB编程计算可以求出其他电阻的转换关系，计算程序的源代码为

该程序运行的结果为

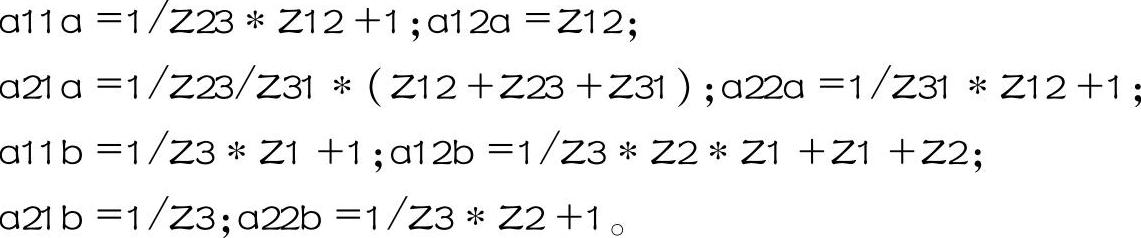
整理可得A参数矩阵相等的条件为

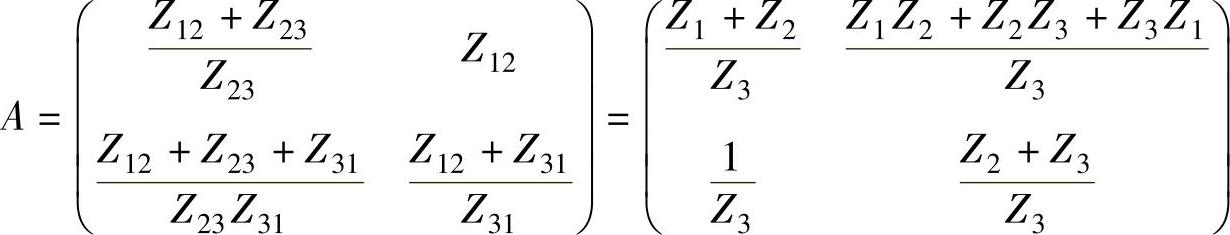
比较系数整理可得л形网络和T形网络，或者T形网络和л形网络等效变换的公式，这些公式与第1章推导的式（1-54）和式（1-55）相同。

【例4-4】 求图4-5所示二端口网络的H参数、A参数和Z参数。

解 图4-5b所示的器件是后续课程将要介绍的晶体管，图4-5a所示的电路是晶体管的H参数模型，根据H参数方程的定义和叠加定理可得

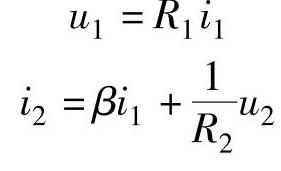
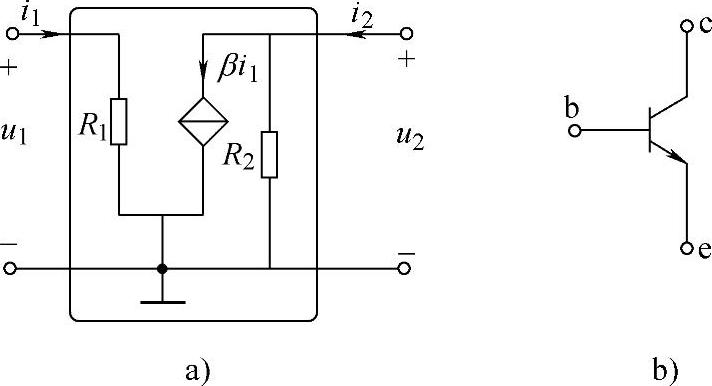
图4-5 晶体管H参数模型

整理可得电路的H参数方程为

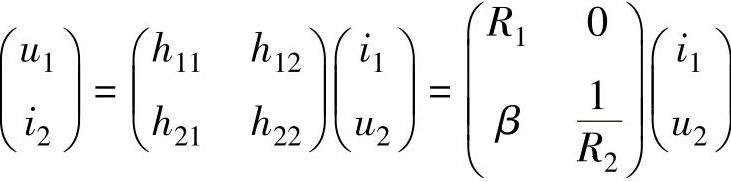
下面来推导H参数方程转Z参数方程的公式

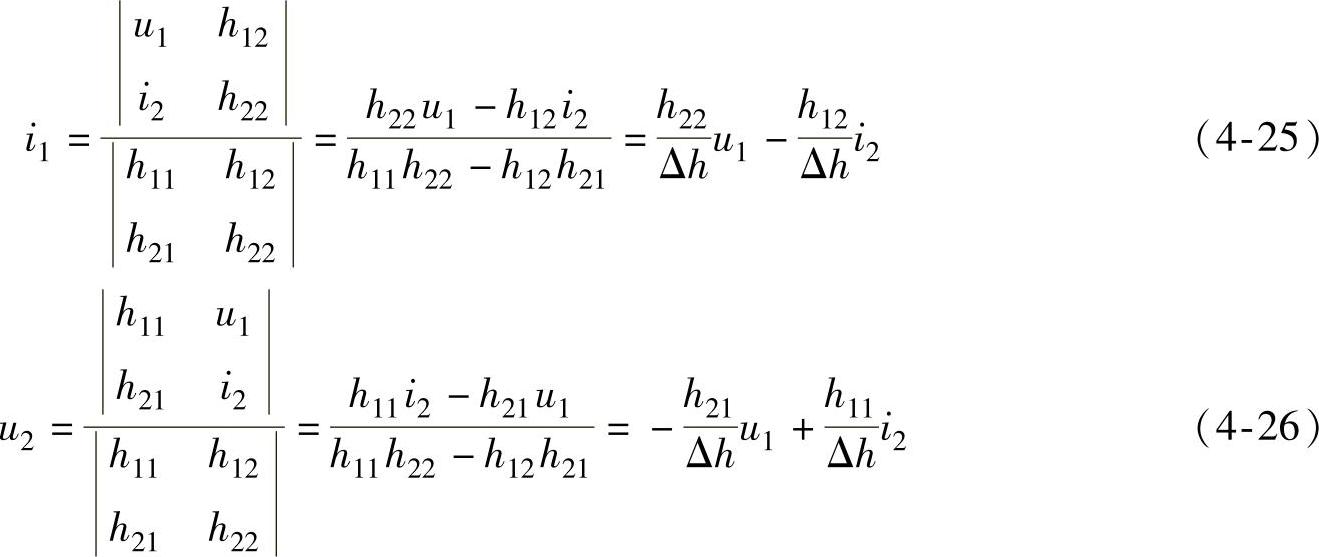
根据式（4-25）可得

将式（4-27）代入式（4-26）可得

将式（4-27）和式（4-28）写成矩阵可得

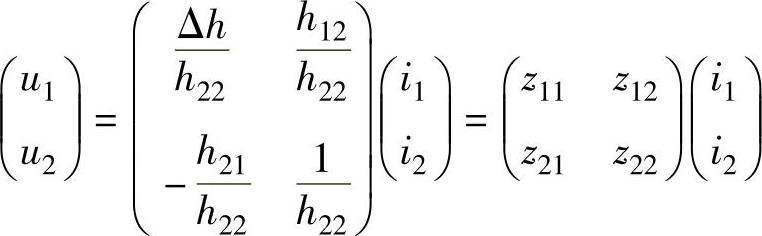
比较系数可得H参数矩阵转换成Z参数矩阵的公式

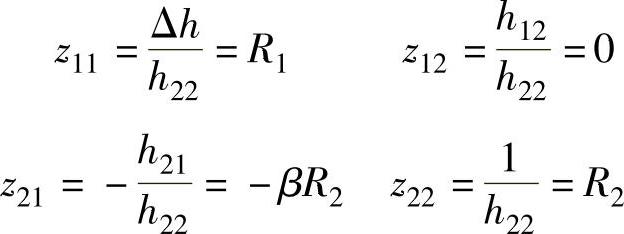
利用Z参数转A参数的公式可得A参数矩阵为

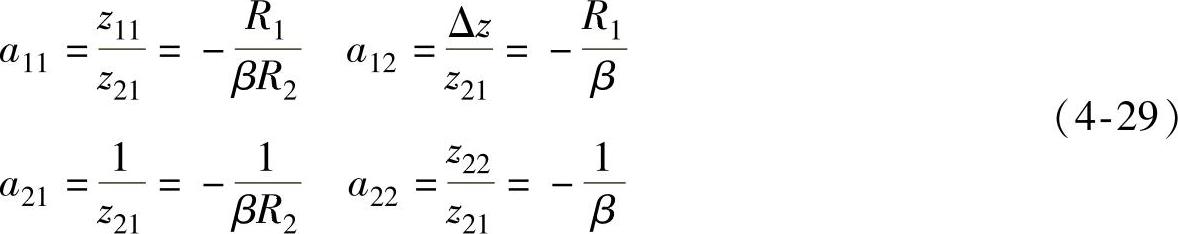
用MATLAB求解的源代码为

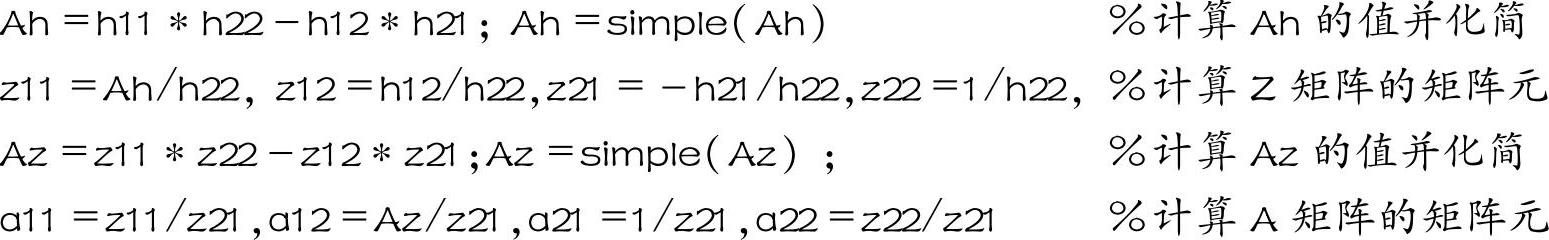
该程序运行的结果为

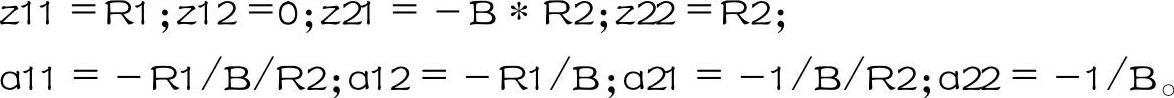
在后续课程中，经常要用到图4-4b所示器件的Y参数方程，根据Y参数方程的定义和叠加定理可得

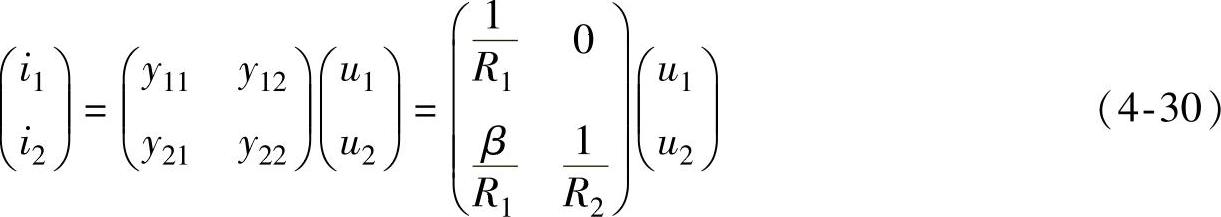
该方程经常用在高频电路的分析和计算中，因为在高频电路中，图4-4a所示二端口网络中的器件与频率有关，Y参数方程中的电阻R₁和R₂必须用阻抗Z₁和Z₂来替代。