高效的RC带通滤波器的介绍

1.电路的组成

所谓的带通滤波器就是允许某个频率范围内的信号通过，而将其他频率信号衰减的电路，在Multisim上搭建的RC带通滤波器的电路如图3-23所示。

比较图3-16、图3-19和图3-23可得，将低通滤波器和高通滤波器串联起来即可组成带通滤波器，图中波特图仪面板上的曲线清晰地显示出电路的带通特性。

2.电压放大倍数和波特图

由图3-23可得，第一个电路的输出电压等于第二个电路的输入电压（U_o1=U_i2），根据电路电压放大倍数的定义可得带通滤波器的电压放大倍数为

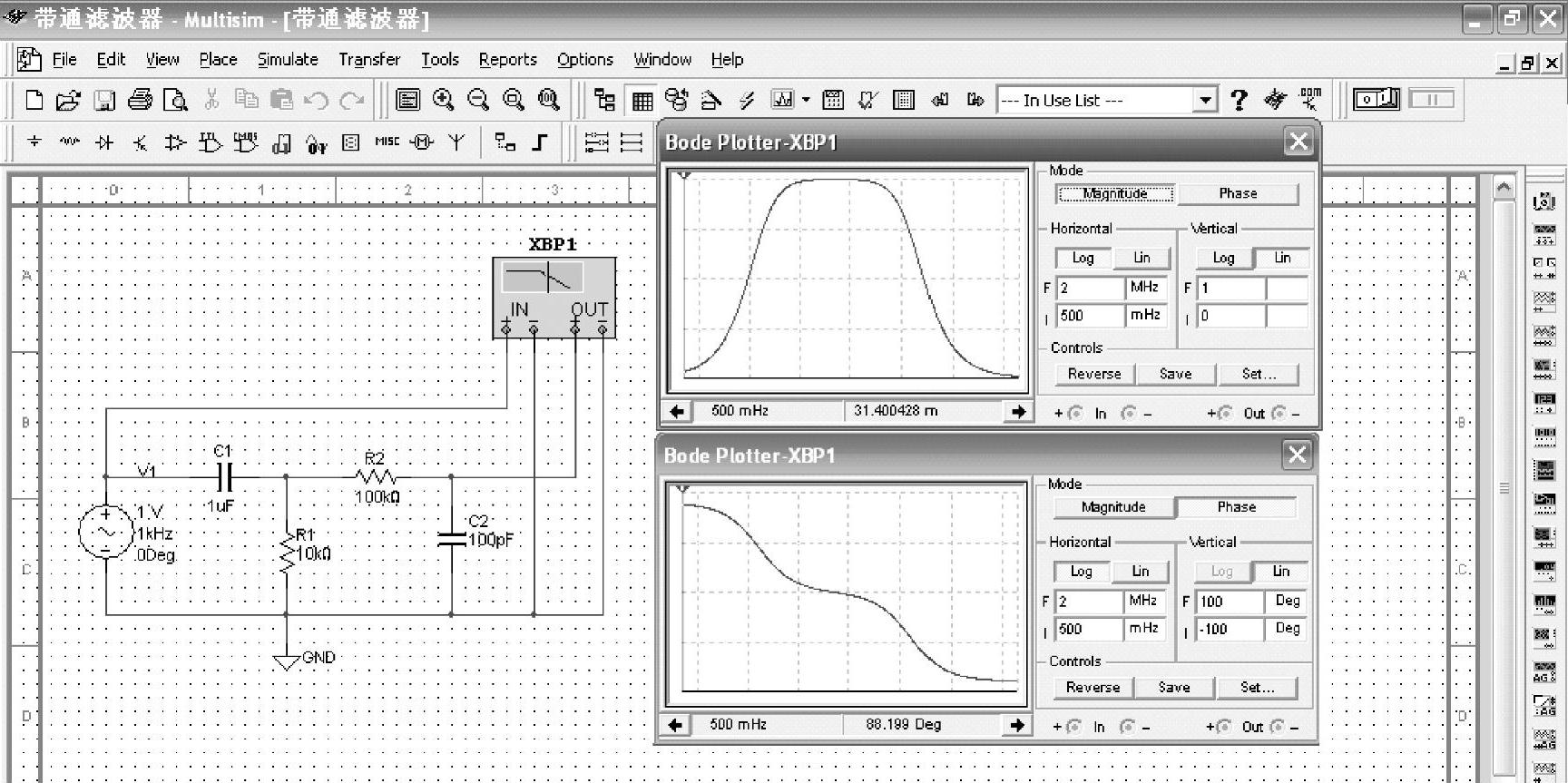
图3-23 RC带通滤波器

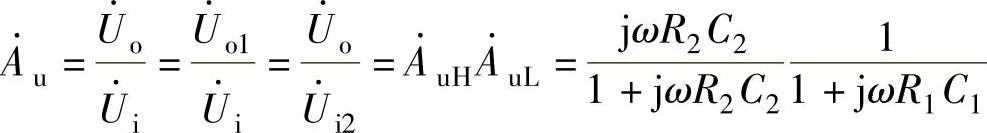
令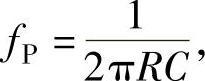则

高通滤波器的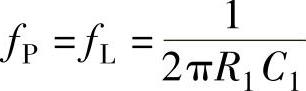，低通滤波器的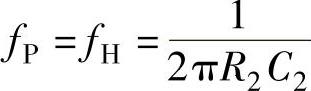

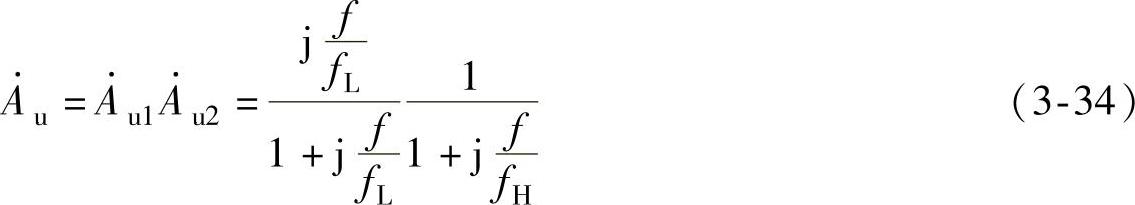
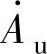的模和辐角为

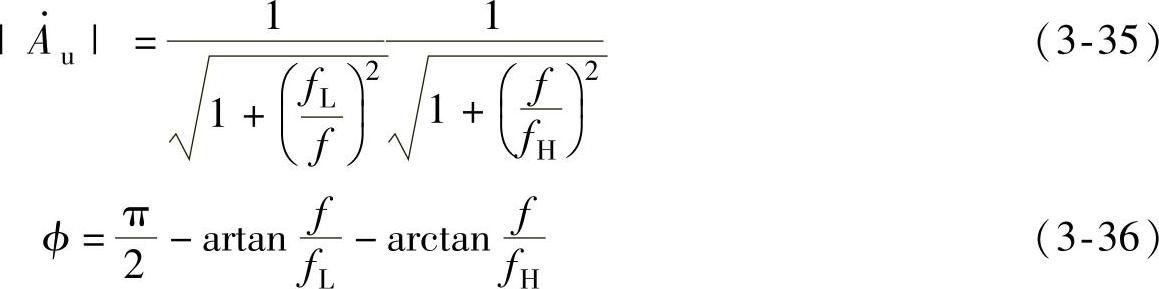
式（3-34）称为带通电路的频响特性，式（3-35）称为带通电路的幅频特性，式（3-36）称为带通电路的相频特性。下面分几种情况来讨论带通滤波的幅频特性。

（1）当f=f_P时

当f=f_P时，式（3-35）变成

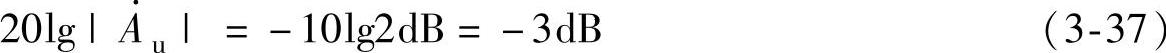
由上式可得通带截止频率f_P的物理意义是：因带通电路的增益随频率的升高或降低而下降，当带通电路的增益下降了3dB时所对应的频率就是f_P。两个截止频率的差是带通滤波器的带宽，即

BW_0.7=f_bw=f_H-f_L （3-38）(www.xing528.com)

（2）当f＜0.1f_L时

当f＜0.1f_L时，式（3-35）中的f_L/f项比10大，公式中的1可忽略，式（3-35）的结果也是一条（-20dB/10倍频）线，即频率每减少10倍，增益下降20dB，说明该电路对低频信号有很强的衰减作用。

（3）当f＞10f_H时

当f＞10f_H时，式（3-35）中的f_H/f项比10大，公式中的1可忽略，式（3-35）的结果也是一条（-20dB/10倍频）线，即频率每增加10倍，增益下降20dB，说明该电路对高频信号有很强的衰减作用。

根据上面讨论的结果，将高通滤波器和低通滤波器的波特图拼在一起可得带通滤波器的波特图，如图3-24所示。

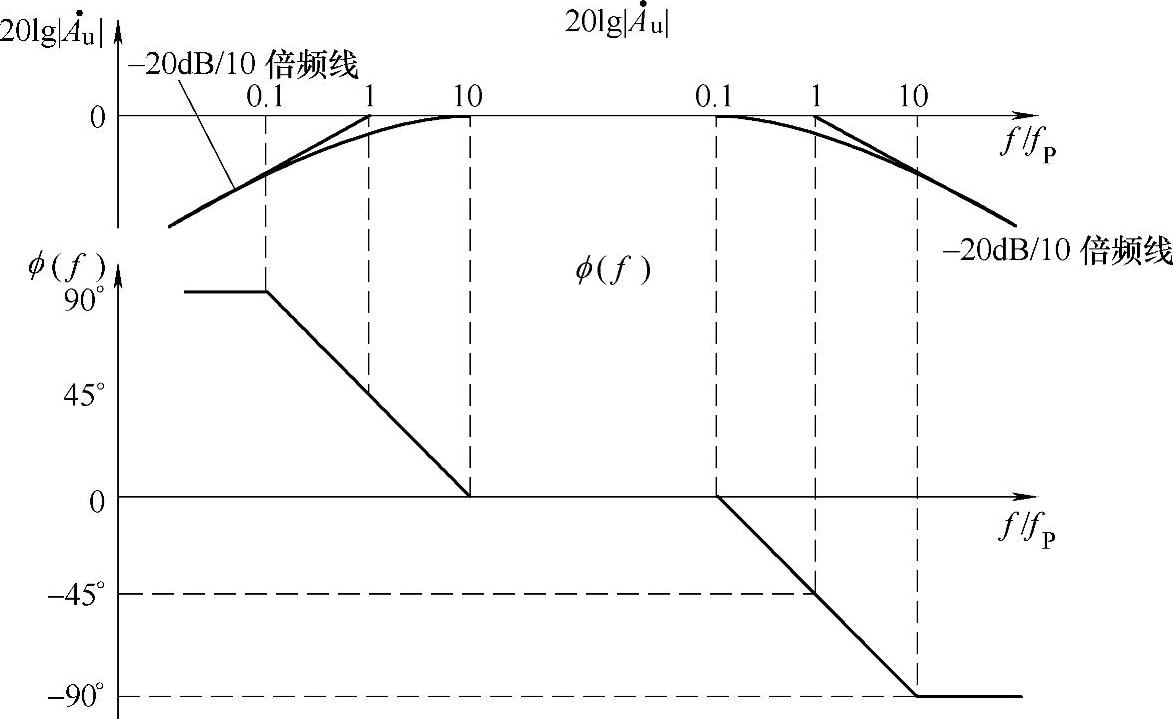
图3-24 带通滤波器的波特图

图3-24的波特图也可以调用MATLAB中画波特图的函数来画，调用MATLAB软件画波特图函数的方法是

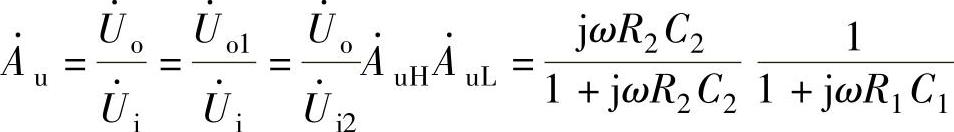
将图3-23所示的电路中R₁=10kΩ，R₂=100kΩ，C₁=1μF，C₂=100pF代入可得

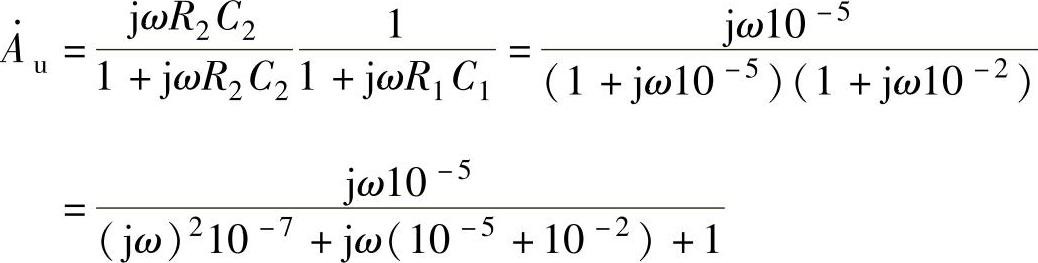
根据上式用MATLAB画波特图的程序为

该程序运行的结果如图3-25所示。

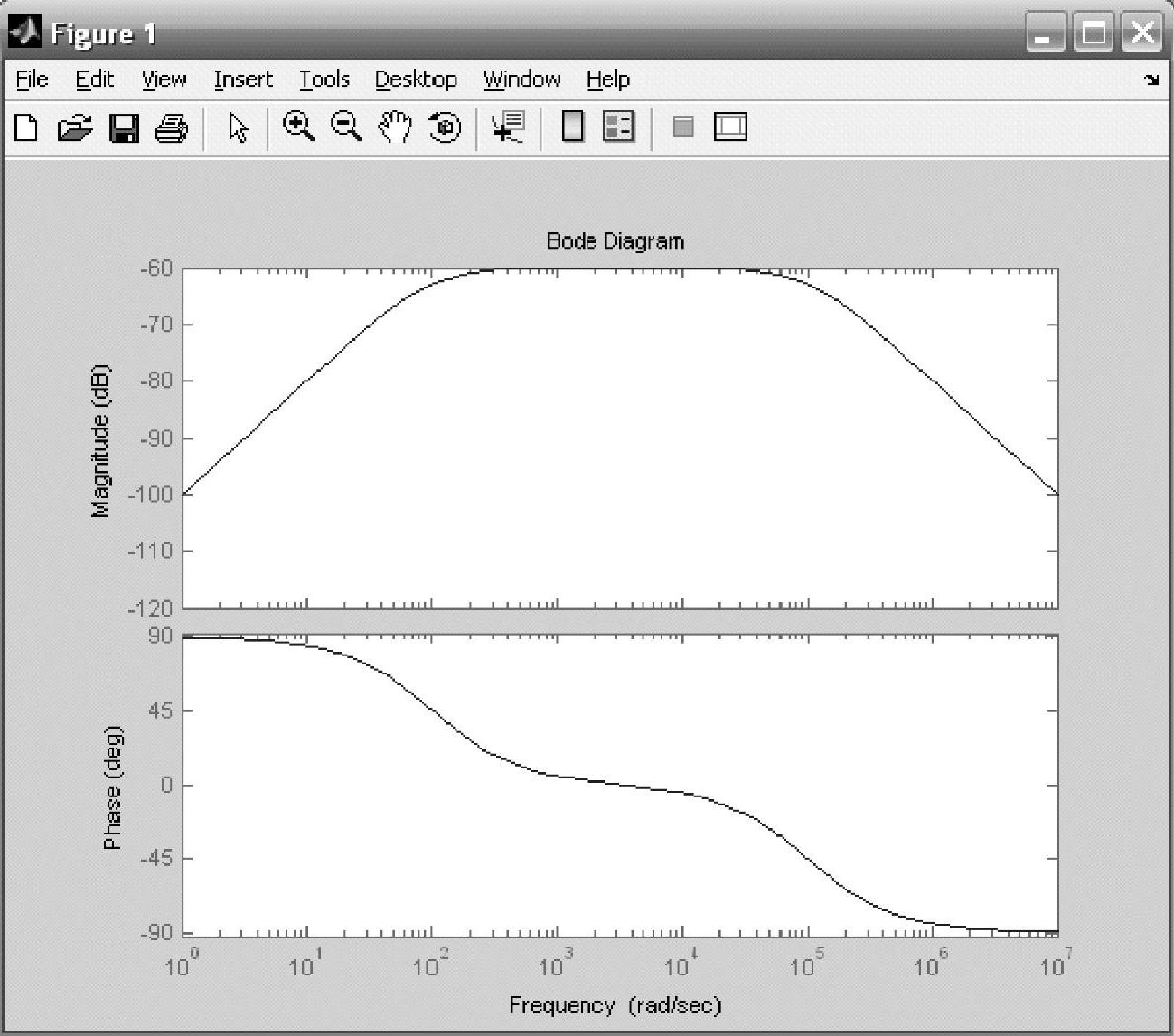
图3-25 用MATLAB画的波特图

综上所述，同样是RC电路，在不同的场合所起的作用完全不一样。在脉冲信号的作用下，RC电路为微分电路、积分电路或阻容耦合电路；在正弦信号的作用下，RC电路可以组成高通滤波器，也可以组成低通滤波器，带通滤波器和带阻滤波器等。利用RC电路的相频特性还可以组成RC移相电路。

讨论RC电路对非正弦信号的响应，可利用傅里叶级数对输入信号进行分解，然后用叠加定理来求解。