如何确定换路定则及初始值？

1.换路

任何电路在特定的条件下都处于一种稳定的状态，在这个状态下，如果电路中的电源、元件的参数、电路的结构或工作状态发生了变化，该电路将由原来的状态转换为另一种状态。上面电路的开关从1拨向2，或者从2拨向1，都使原电路的状态发生了变化。这种因电路的结构或参数的变化所引起的电路变化统称为“换路”。

2.换路定则及初始值的确定

动态电路之所以会产生暂态过程，其理论根据是能量的变化不能突变。能量的积聚和衰减是需要时间的，否则相应的功率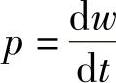将趋于无限大，这是不可能的。

例如前面所举的RC或RL电路，因为电路中有储能元件电容或电感，电路换路以后，电路中的能量也将发生变化，但是电源输出的功率是有限值，因此，电容元件中的电场能量和电感线圈中的磁场能量不会因换路而突变，因电容器所储存的能量与电容器两端的电压u_C有关，电感器所储存的能量与流过电感的电流i_L有关，所以，电容器两端的电压u_C和流过电感线圈中的电流i_L都不会因换路而突变。

在研究电路问题时，通常将换路的时刻定为t=0的时刻。为了叙述方便，把刚开始换路前的瞬间记为t=0_-，把换路刚结束后的瞬间记为t=0₊，换路所经历的时间是从0_-到0₊。根据储能元件电容的电场能量和电感的磁场能量不能突变的理论可得，在t=0_-到t=0₊的换路瞬间，电容元件两端电压和电感元件中的电流不能突变，这就是换路定则。换路定则的公式为

必须指出的是，换路定则只能确定换路瞬间，t=0时不能突变的u_C和i_L的初始值，而i_C和u_L以及电路中其他元件的电压、电流的初始值是可以突变的，如流过电容的电流和电感两端的电压都是可以突变的。

由换路定则确定了u_C（0₊）或i_L（0₊）初始值后，电路中其他元件的电压、电流的初始值可按以下的原则来确定：

1）换路瞬间，电容元件当作恒压源。如果u_C（0_-）=0，则u_C（0₊）=0，电容元件在换路的瞬间相当于短路。

2）换路瞬间，电感元件当作恒流源。如果i_L（0_-）=0，则i_L（0₊）=0，电感元件在换路的瞬间相当于开路。

3）运用KCL、KVL及直流电路中的分析方法，可计算电路在换路的瞬间其他元件的电压、电流的初始值。

下面举几个利用换路定则确定初始条件的例子。

【例3-2】 利用换路定则确定例3-1解中的积分常数。

解 根据换路定则可得开关S从2拨向1时的初始条件为

分别将式（3-10）和式（3-11）代入式（3-2）和式（3-5）可得

将A的表达式代入式（3-2）和式（3-5）中可得

上面两式说明，电压u_C（t）和电流i_L（t）都是按照同样的指数规律衰减，它们衰减的快慢程度取决于时间常数г的大小，г由电路的结构和元件的参数来确定，它的大小反映了一阶电路过渡过程进展的速度，是反映过渡过程特征的一个物理量。

根据换路定则可得开关S从1拨向2时的初始条件为

分别将式（3-14）和式（3-15）代入式（3-4）和式（3-7）可得

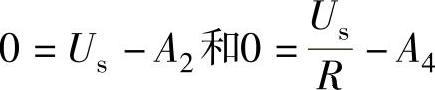
则(www.xing528.com)

将A的表达式代入式（3-4）和式（3-7）可得

上面两式说明，电压u_C（t）和电流i_L（t）都是按照同样的指数规律上升，它们上升的快慢程度同样取决于时间常数г的大小。

设U_s=10，I_s=10，г₁=0.5，г₂=0.25。根据式（3-12）、式（3-13）、式（3-16）和式（3-17）用MATLAB画电路电压、电流随时间变化的波形图的程序为

该程序运行的结果如图3-3所示。

式（3-12）和式（3-13）函数的图像分别对应于图3-3中的两张放电曲线，其中左边曲线的时间常数г₁大于右边曲线的时间常数г₂，所以，右边的曲线较左边的曲线衰减得快。

根据电容C或电感L放电过程的曲线和电路可见，该过程所描述的状态都是动态电路在没有外加激励信号时，由电路中动态元件的初始储能所引起的响应，这种响应在电路分析的课程中称为零输入响应。

式（3-16）和式（3-17）函数的图像分别对应于图3-3中的两张充电曲线，其中左边曲线的时间常数г₁大于右边曲线的时间常数г₂，所以，右边的曲线较左边的曲线上升得快。

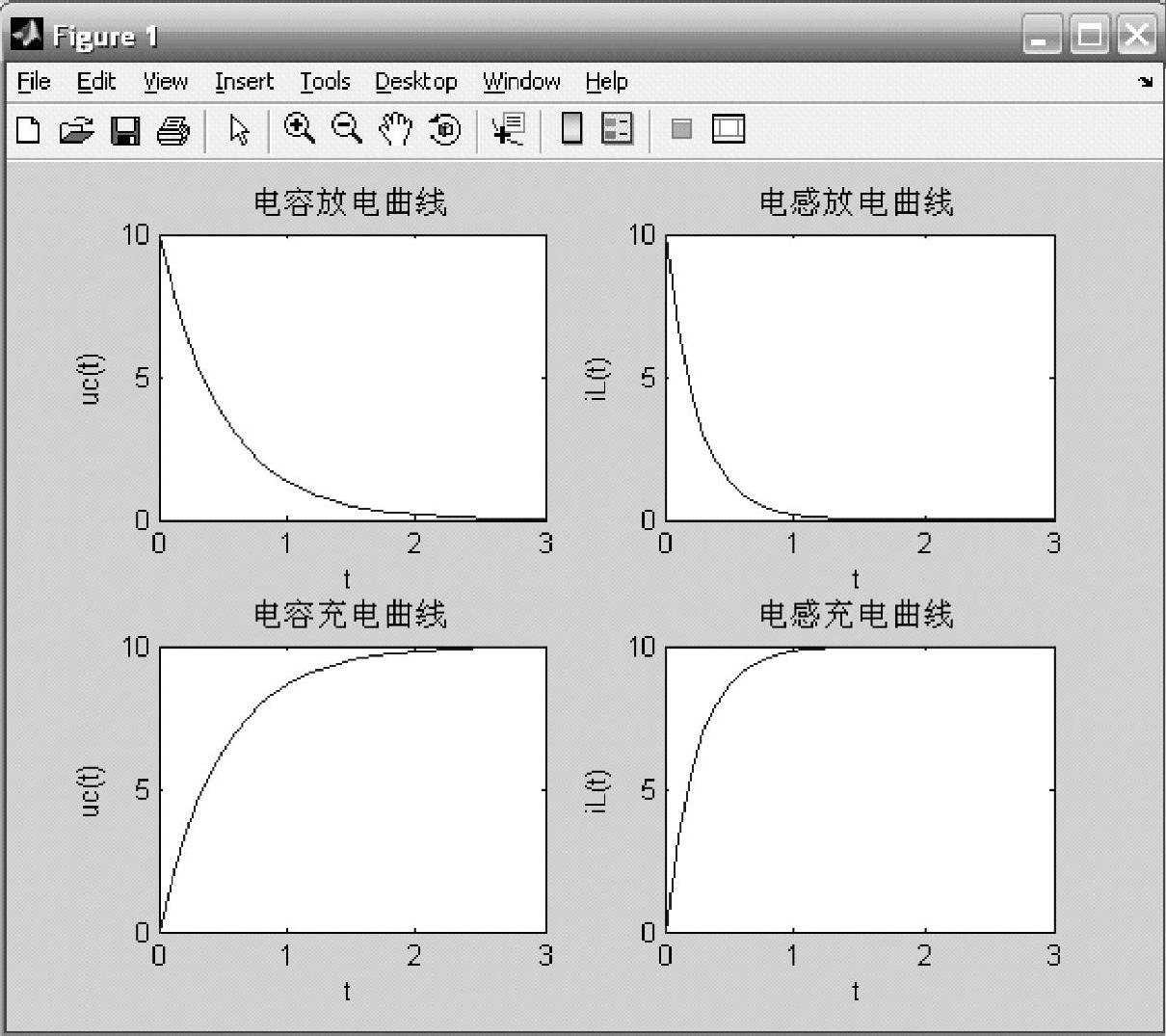
图3-3 动态电路的工作波形图

由电容C或电感L充电过程的曲线和电路可见，该过程所描述的状态都是动态电路在没有初始储能的情况下，由外加激励信号U_s或I_s所引起的响应，这种响应在电路分析的课程中称为零状态响应。零输入响应和零状态响应的和称为动态电路的完全响应。

【例3-3】 确定图3-4所示电路开关S闭合后各支路电流和电压的初始值。设开关S闭合前电容元件和电感元件上均未储存能量。

解 先求出S闭合前瞬间各支路电流和电压的初始值，根据已知的条件在t=0-的瞬间，因开关S未闭合，电容和电感上均未储能，所以，u_C（0_-）=0，i_L（0_-）=0，可将电容作短路处理，电感作开路处理，由此可得t=0-瞬间的等效电路，如图3-5所示。由图3-5可见，除U_s=10V外，所有元件上的

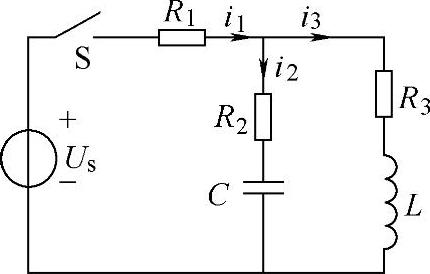
图3-4 例3-3图

电压和电流均为零。

将图3-5所示电路的开关S闭合，就成为开关S闭合瞬时的等效电路，此电路就是换路后初始瞬间的电路结构。因为换路瞬间电容两端的电压和电感上的电流不能突变，所以电容元件和电感元件仍分别以短路和开路处理。根据图3-5可得

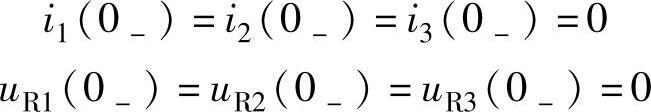
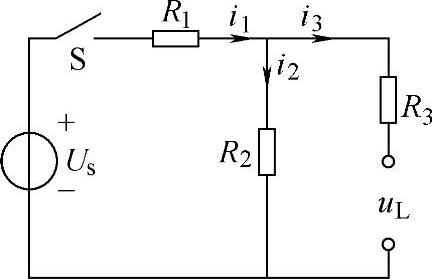
图3-5 t=0_-时的等效电路

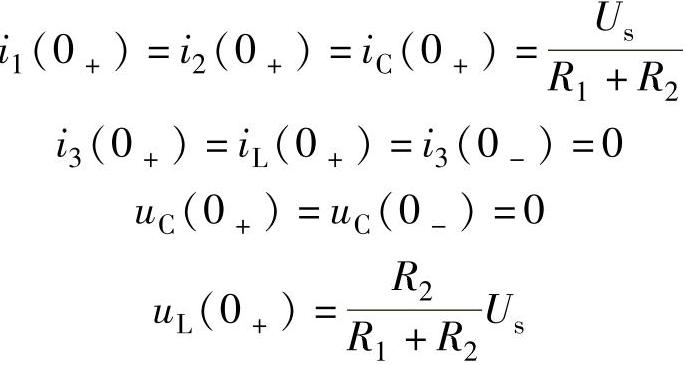
从计算的结果可见，换路瞬间电容上的电流和电感两端的电压不等于0，发生了突变，而电容两端的电压和电感上的电流等于0，不发生突变。