动态电路方程的推导

对于含有一个电容和一个电阻，或一个电感和一个电阻的电路，当电路的无源元件都是线性时不变时，描述电路参数的方程将是一阶线性常微分方程，相应的电路称为一阶电阻电容电路（简称RC电路）如图3-1a所示，或一阶电阻电感电路（简称RL电路），如图3-1b所示。

图3-1 一阶电路

如果电路仅含一个动态元件，利用戴维南定理，可以将动态元件以外的电路等效成电压源和电阻相串联的组合，从而将原电路等效成如图3-1所示的RC或RL电路，这样的电路称为一阶动态电路。

动态电路的一个特征是当电路的结构或元件的参数发生变化时，可能会使原来电路的工作状态发生改变，这种改变需要经历一个过程，动态电路所经历的变化过程称为暂态过程，或过渡过程。

动态电路的经典分析法是：根据KVL和KCL建立描述电路参数变化的微分方程，然后求解该微分方程，确定电路的参数随时间变化的函数关系。

【例3-1】 试分别求出图3-2a和图3-2b所示两电路中，将开关S从2拨向1，电路处于稳态后，又将S从1拨向2这两个动态过程，电容两端的电压u_C和电感上的电流i_L随时间变化的函数关系。

图3-2 例3-1图

解 开关S从2拨向1后，电压源U_s没有加在RC电路上，RC电路在电容器储存电能的激励下电压和电流将发生变化，设电路电流和电压的参考方向为关联，由KVL可得

u_R+u_C=0

将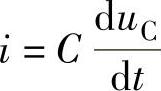的关系式代入可得

上式是可分离变量的一阶线性常系数微分方程，对上式进行分离变量可得

两边取积分得

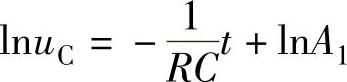
上式中的lnA₁是积分常数，令г=RC，г称为时间常数，去掉上式中的对数可得

式（3-2）就是开关S从2拨向1后，电容两端的电压随时间变化的函数关系式，式中的A₁为积分常数。

当开关S从1拨向2以后，电压源U_s加在RC电路上，RC电路的电流和电压又将发生变化，利用KVL可得

u_R+u_C-U_s=0

将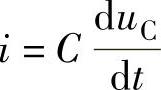的关系代入可得

式（3-3）也是可分离变量的一阶线性常系数微分方程，对上式进行分离变量可得(www.xing528.com)

解此微分方程可得

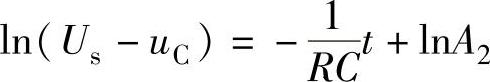
上式中的lnA₂也是积分常数，去掉上式中的对数可得

式（3-4）就是开关S从1拨向2后电容两端的电压随时间变化的函数关系式，式中的A₂也是积分常数。

对于RL电路，当开关S从2拨向1后，利用KVL可得

u_R+u_L=0

将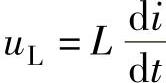的关系代入可得

上式的形式与式（3-1）一样，解的方法也一样，令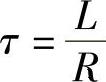，г也称为时间常数，可得

当开关S从1拨向2以后，利用KVL可得

u_R+u_L-U_s=0

将的关系代入可得

该微分方程的形式与式（3-3）一样，解的方法也一样，分离变量可得

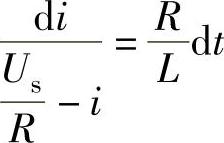
式（3-5）和式（3-7）也是两个动态过程，它们是描述电感上的电流随时间变化的函数关系式，式中的A₃和A₄也是积分常数。

用MATLAB也可以进行微分方程求解的计算，用MATLAB求解上述两个微分方程的程序为

在式（3-2）、式（3-4）、式（3-5）和式（3-7）中都有一个积分常数A，该常数可由电路的初始条件来确定，电路的初始条件可以根据电路在换路瞬间所处的状态来确定。