谐振电路中负载和电源内阻的影响分析

图2-55所示的谐振电路不带负载，且电源为理想的电压源，处于这种状态下的谐振电路称为空载。谐振电路处于带负载和信号源内阻不能忽略的状态称为加载。为了讨论加载对谐振电路性能的影响，用符号Q₀表示谐振电路空载状态下的品质因数，用符号Q表示谐振电路加载状态下的品质因数。

处在加载状态下的谐振电路如图2-56a所示，为了讨论电路的方便，通常利用对偶定理将图2-56a所示的电路置换成图2-56b所示的形式，图2-56c为图2-56b所示电路的等效电路。利用对偶定理将式（2-88）所描述的表达式置换成

图2-55 RLC并联谐振电路

图2-56 加载情况下的谐振电路

式（2-89）中的G为电感线圈内阻R的电导，根据式（2-89）和并联电路计算总电导的关系式可得谐振电路加载后的Q值为

因为式（2-90）中的G′大于式（2-89）中的G，所以谐振电路加载后的Q值将减小。图2-52说明，谐振电路Q值的变化，将影响谐振电路的通频带和选择性。为了减少加载对谐振电路Q值的影响，要求负载和电源满足功率匹配的条件G_L=G_S，通常这个条件不能自然地得到满足，可以利用各种阻抗变换的方法实现，以减少加载对谐振电路Q值的影响。常见的阻抗变换电路是变压器耦合、电感分接电路和电容分接电路，如图2-57所示。

图2-57a中负载R_L与谐振电路的耦合是变压器耦合，信号源与谐振电路的连接是电感分接电路，图2-57b中负载R_L与谐振电路的连接是电容分接电路。

变压器耦合和电感分接电路是利用变压器阻抗变换的原理，实现负载或信号源的内阻与谐振电路的阻抗相匹配的目的，例2-10已经讨论了阻抗变换的问题，下面来讨论电容分接电路实现阻抗变换的原理。图2-57b电容分接电路将电压源换成电流源后的电路如图2-58a所示，图2-58b所示的电路是电容分接电路的等效电路。

在图2-58a中，根据例2-10的结论可得电容分压阻抗变换的关系为

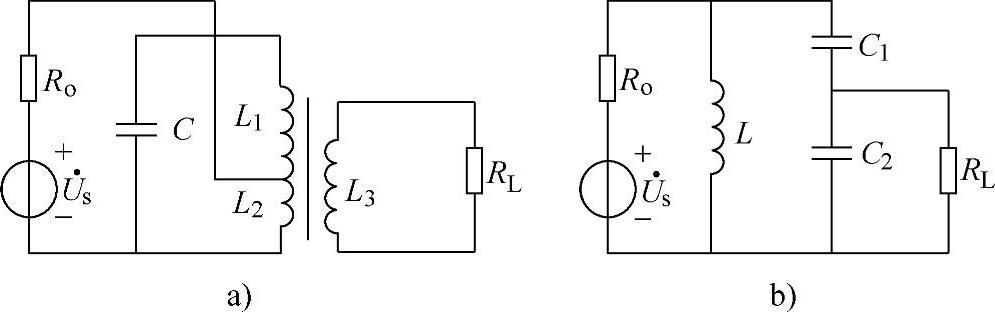
图2-57 实现阻抗匹配的谐振电路

图2-58 电容分接的谐振电路

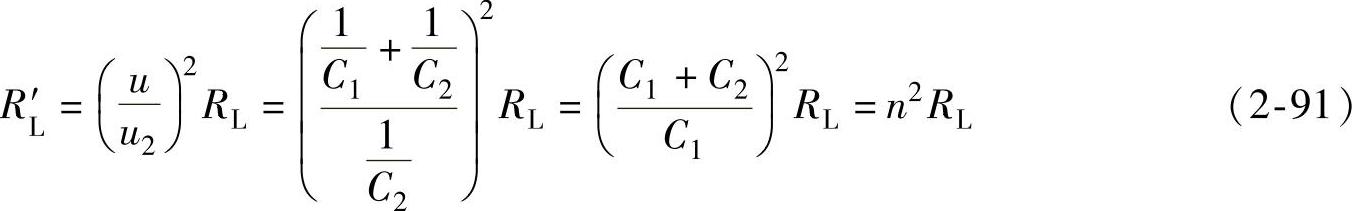
式中，R_L′=n²R_L为负载电阻R_L接成图2-58b所示形式下的等效电阻，表示电容分接阻抗变换的作用和变压器阻抗变换的作用相类似，计算的公式也相同。

谐振电路加载对Q值的影响在Multisim软件上仿真实验的结果如图2-59所示。

在图2-59中，左边的电路显示出加载使谐振电路的Q值减小，第一个波特图仪显示出谐振曲线的幅度较小，通频带较宽，选择性较差；右边的电路显示出采用电感和电容分接电路可减小加载对谐振电路Q值的影响，第二个波特图仪显示出谐振曲线的幅度较大，选择性较好。

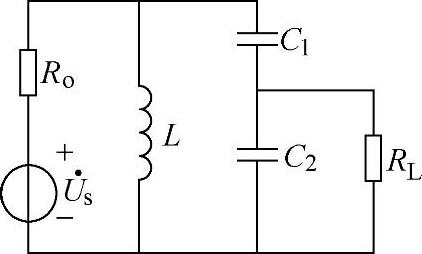
【例2-15】 在如图2-60所示的电路中，设C₁=1000pF，C₂=2000pF，L=20μH，R_L=1kΩ，求信号源的内阻R_o的值、谐振电路品质因数和带宽。

解 由图可知，谐振电路的总电容C是两个电容相串联的值，根据串联电容的计算公

式可得

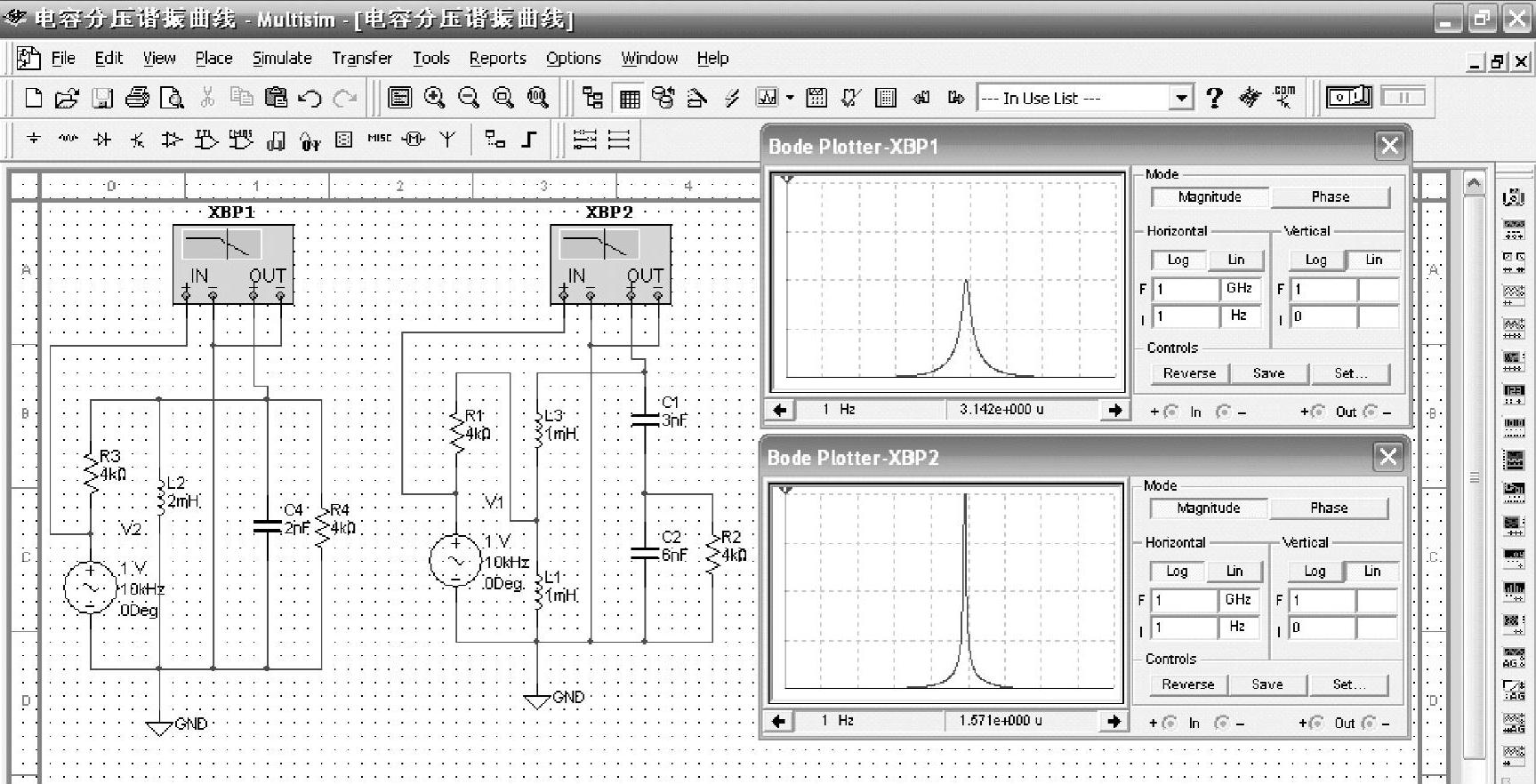
图2-59谐振电路加载对Q值的影响

根据谐振频率的计算公式可得

(www.xing528.com)

图2-60 例2-15电路图

根据式（2-91）可得

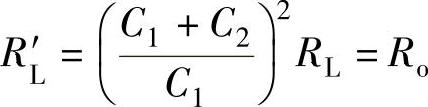
电路的总电阻R为

谐振电路的有载品质因数Q和带宽BW_0.7为

用MATLAB进行计算的程序为

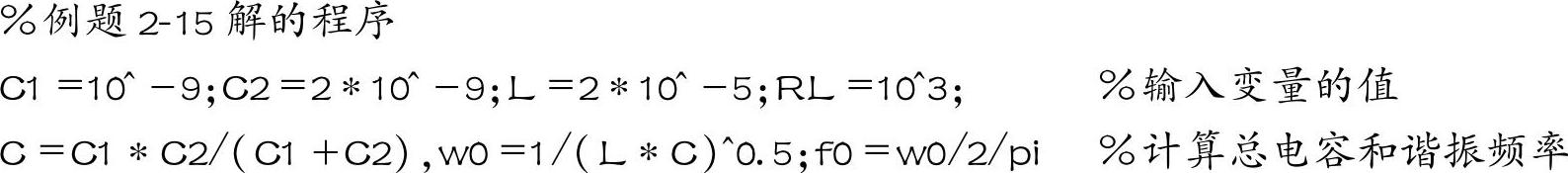
该程序运行的结果为

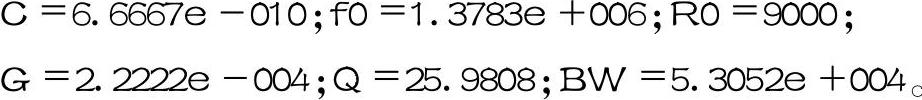
解得结果用Multisim软件仿真验证的结果如图2-61所示。

图2-61 用Multisim软件仿真验证的结果

拖动图2-61中波特图仪屏幕上的测量标尺可以验证理论计算结果的正确性。

在电子技术中，常利用并联谐振电路阻抗高的特点，在LC并联谐振电路的两端获得处于谐振状态下，f=f₀信号的较高电压，以实现选频的目的。图2-62a所示的电路就是高频电路中谐振放大器的选频电路，利用该电路可以将无线电广播中465kHz的中频信号选出来。

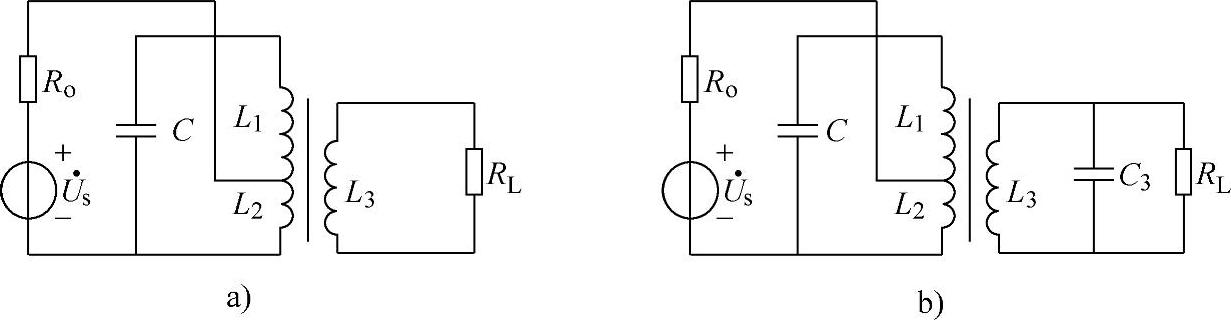
图2-62 双调谐谐振电路

在图2-62a所示的电路中，谐振电路只有一个，称为单调谐回路。单调谐回路的选择性和通频带宽度是一对矛盾，选择性好的，通频带宽度就窄；选择性差的，通频带宽度就宽。在要求通频带宽度较大的场合可以采用双调谐回路，双调谐回路的电路结构如图2-62b所示。

比较图2-62a和图2-62b所示的电路可得，两个电路的主要差别在谐振回路的数量上，单调谐电路只有一个谐振回路，而双调谐电路有两个谐振回路。双调谐回路通常采用参差调谐的技术来增大谐振回路的通频带，根据参差调谐技术的原理，用MATLAB编写的画谐振曲线的程序为

该程序运行的结果如图2-63所示。

由图2-63可见，用参差调谐技术实现双调谐的原理是：在双调谐回路中，两个谐振回

图2-63 双调谐回路的谐振曲线

路的谐振频率调在差别很小的两个不同点上，回路总的谐振曲线是两个谐振回路谐振曲线的和。

由图2-63可见，双调谐回路谐振曲线的特点是：频带的宽度宽，通带内的传输特性很平坦，通带外衰减的特性很陡峭，接近理想带通的选频特性。