RLC串联谐振优化技巧

RLC串联电路如图2-51a所示，图2-51b是该电路的相量图。当电路中的X_L=X_C时，阻抗角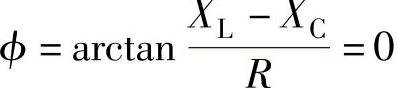，即电路的电压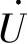和电流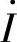同相，这种现象称为RLC串联谐振。下面来讨论RLC串联谐振电路的特点。

1.串联谐振的条件和固有频率

由上面的分析可知，当电路的电压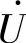和电流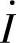同相时，RLC串联电路发生串联谐振的现象。电路电压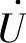和电流同相的条件是X_L=X_C，该条件就是串联谐振的条件。

由串联谐振的条件可得，串联谐振时电源频率f与电路参数之间的关系为

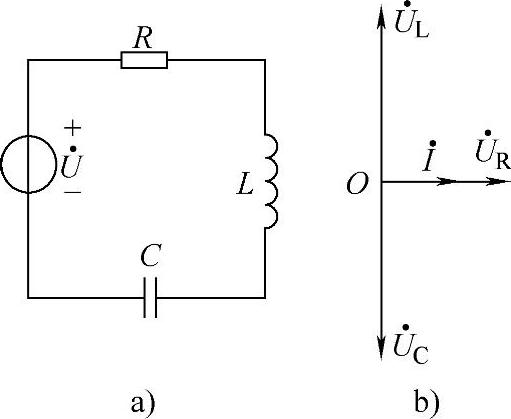
图2-51 RLC串联谐振电路

式中，f₀称为谐振电路的固有频率，f₀由电路的参数确定。当电源频率f不变时，只要调节电路的参数L或C，f₀就发生相应的变化，当f₀=f时电路产生谐振。或者电路参数不变，改变电源的频率f使之与f₀相等，电路也会发生谐振。

2.串联谐振电路的特点

1）谐振发生时，因X_L=X_C，所以阻抗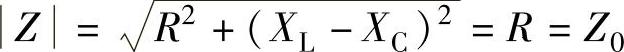达到最小值，电路呈电阻性。

2）在电压U不变的情况下，电路中的电流I=I₀=U/R达到最大值，I₀称为谐振电流。

3）由于谐振时X_L=X_C，所以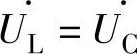，而和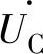的相位相反，相加时互相抵消，所以电阻上的电压等于电源的电压U，即

U_R=I₀R=U （2-68）

电感和电容上的电压分别为

式中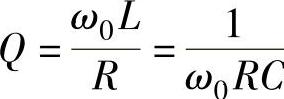，称为RLC串联电路的品质因数，Q是一个无量纲的量，它的物理意义是谐振电路的储能与耗能之比，描述了谐振电路的感抗（容抗）与电阻的比。Q值的大小反映了谐振电路的性能，在感抗或容抗远大于电阻R的情况下，Q将远大于1，根据式（2-70）可得

又因为U_R=U，所以

式（2-71）说明在串联谐振的情况下，有可能会出现U_L（U_C）远大于电源电压U的现象，因此，串联谐振又称为电压谐振。

在分析RLC串联谐振电路的特性时，除了应分析电路的阻抗特性外，还应分析电路的电流和电压随频率变化的关系，这种关系称为RLC串联谐振电路的频率特性。

RLC串联谐振电路的频率特性为复数关系，可以用幅频特性（幅度随频率变化的特性）和相频特性（相位随频率变化的特性）来描述这种复数的关系。描述RLC串联谐振电路幅频特性的曲线又称为谐振曲线。

为了突出电路的幅频特性，谐振曲线常用输出量（u_R或u_L）和输入量（U）比值的频率特性来表示。取U_R/U的频率特性为RLC串联谐振电路的谐振曲线，根据RLC串联谐振电路复阻抗的表达式可得

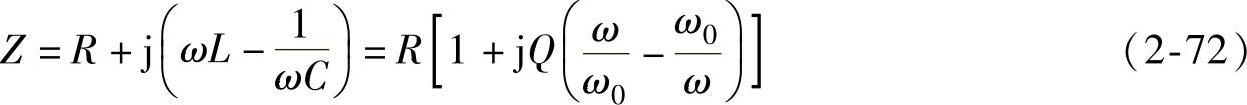
式（2-72）乘电流相量，并将其表示成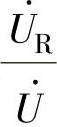的形式可得

式（2-73）幅度随频率变化的特性曲线即为谐振曲线，由此可得描述RLC谐振电路谐振曲线的公式为(www.xing528.com)

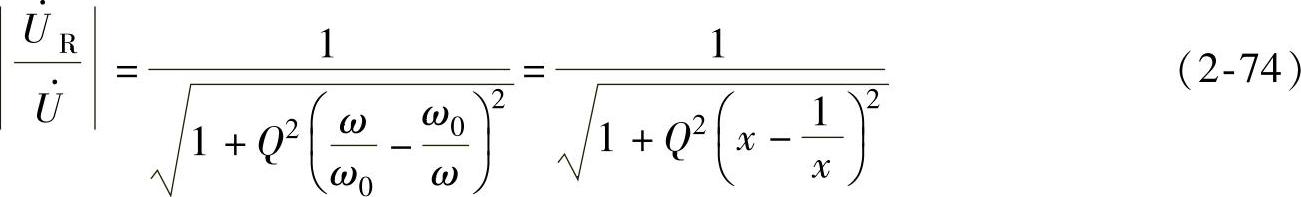
根据式（2-74）用MATLAB编写的画图程序为

该程序运行的结果如图2-52所示。

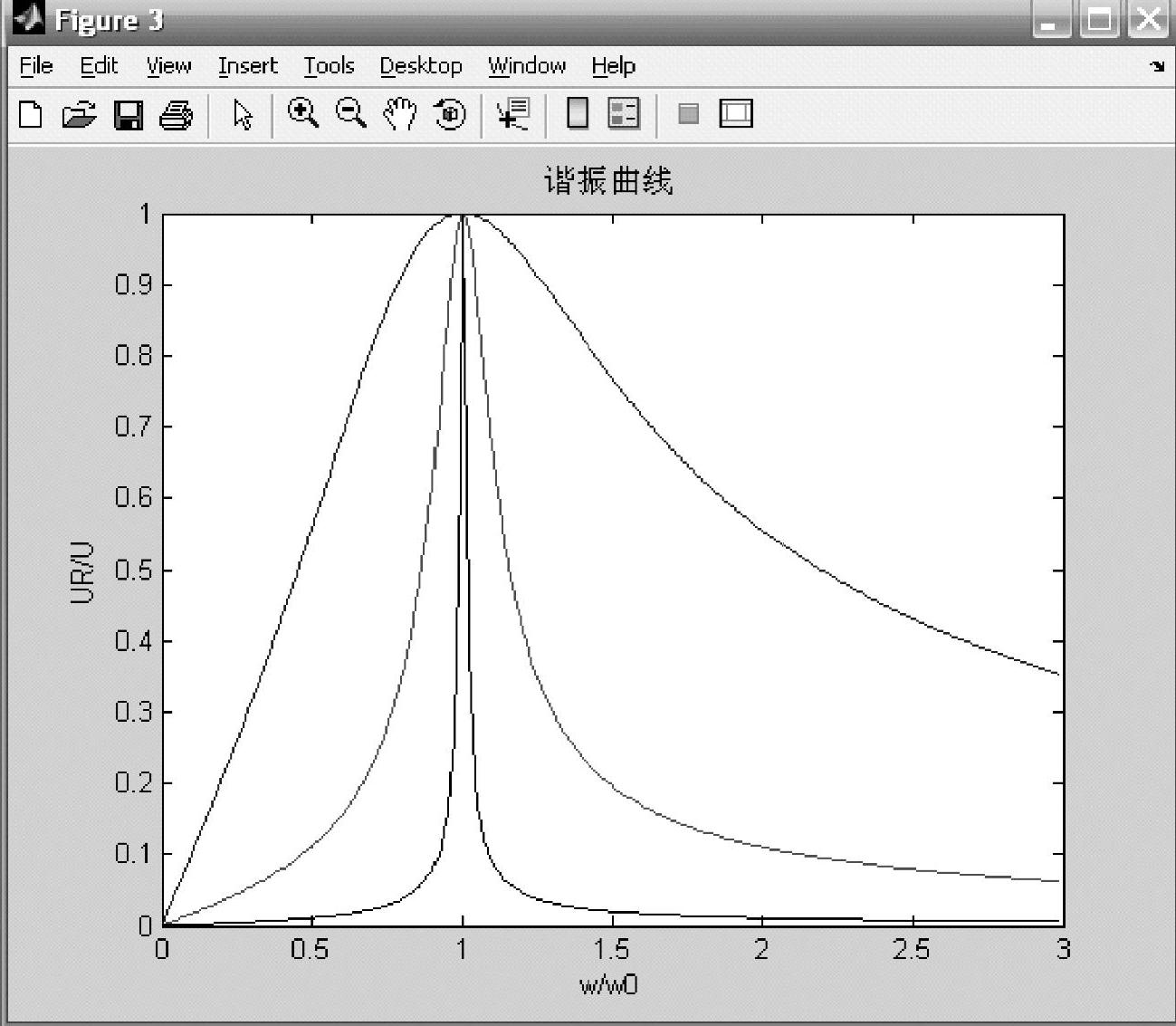
图2-52 串联谐振电路的谐振曲线

图2-52给出了三种不同Q值的谐振曲线。由图2-52可见，RLC串联谐振电路的谐振曲线具有明显的选择性。

谐振曲线的选择性描述了谐振回路从含有各种不同频率的信号中选出有用的信号、抑制干扰信号的能力。

由图2-52可见，RLC串联谐振电路在谐振点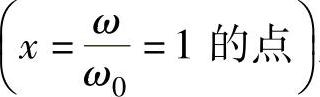上谐振曲线有最大值，当频率偏离谐振点时，曲线逐渐下降，下降的速度随Q值的不同而不同。Q值越大，下降的速度越快，选择性越好。工程上将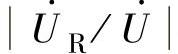的值下降到原值的0.707时，所对应的两个频率ω₂和ω₁称为谐振电路的通带截止频率，两频率的差称为谐振电路的通频带宽度f_BW，通常用BW_0.7来表示

BW_0.7=f_BW=f₂-f₁ （2-75）

根据式（2-75）和f_BW的定义可得

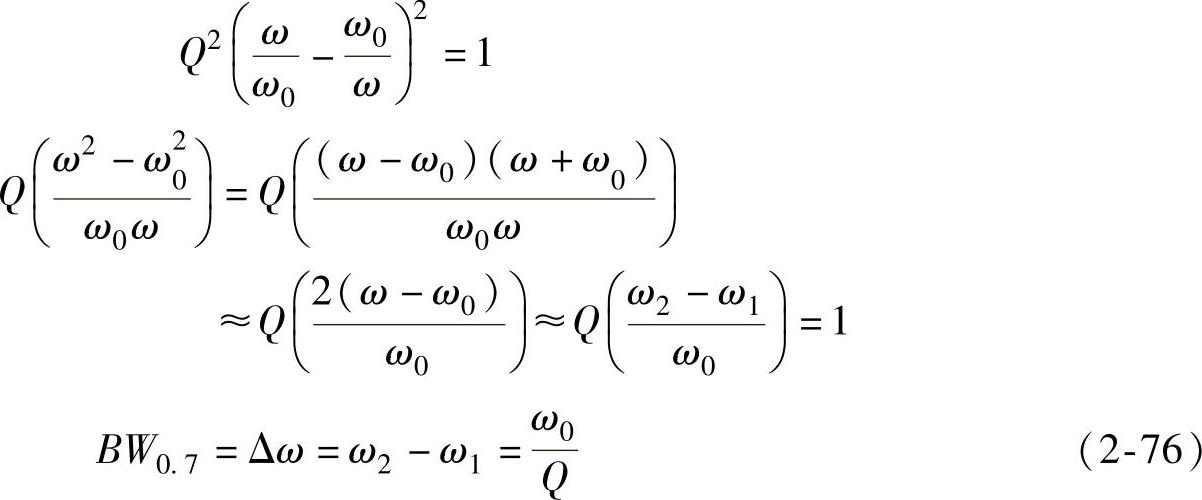
由图2-52可见，谐振电路的选择性和通频带宽度是一对矛盾。选择性好的，通频带宽度就窄；选择性差的，通频带宽度就宽。

在实际应用中，选择性常用谐振回路的幅频特性下降到0.1时的频带宽度BW_0.1来表示，BW_0.1越小，回路的选择性越好。计算频带宽度BW_0.1的示意图如图2-53a所示。为了提高选择性，降低频率失真，要求谐振回路的幅频特性是如图2-53b所示的矩形。

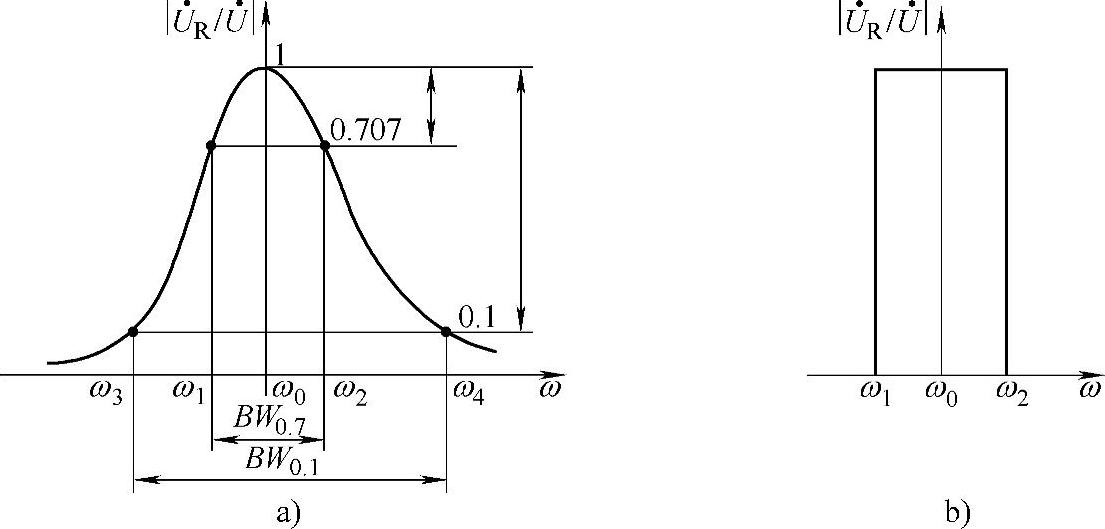
图2-53 谐振电路的谐振曲线

由于实际谐振回路的谐振曲线均不可能是矩形，为了说明实际谐振回路的谐振曲线接近矩形的程度，引入“矩形系数”D的概念。“矩形系数”的定义为

矩形系数的定义说明，矩形系数越接近于1，谐振回路的幅频特性就越接近矩形，回路的选择性也越好。谐振电路的选择性和通频带宽度是一对矛盾，单调谐回路的选择性和通频带宽度如果不能满足要求，可以采用多调谐回路，使谐振回路的选择性和通频带宽度满足一定的要求。

串联谐振的现象在电力工程中应避免，这是因为当串联谐振发生时，电感线圈或电容元件上的电压将增高，可能导致电感线圈或电容器绝缘层被击穿。但在无线电工程中，利用串联谐振现象的选择性和所获得的较高电压，可将所需要接收的高频载波信号提取出来。

例如，收音机的输入电路就是一个由电感线圈（线圈电阻为R）与可变电容器C组成的串联谐振电路，如图2-54所示。

该电路的工作原理是：当各地电台所发射的不同载波频率的无线电波信号被天线线圈L₁接收后，经电磁感应作用，在线圈L上将感应出不同频率的电动势e（f₁）、e（f₂）、e（f₃）等。这些电动势就是RLC串联谐振电路的信号源。

调节可变电容器的电容C，可以改变RLC串联谐振电路的固有频率f₀，使它与欲选电台的载波频率f₁相等，这时电路对e（f₁）信号的阻抗最小，相应的电流I₀最大。因而在电容器两端可获得较高的输出电压，而对于e（f₂）、e（f₃）等信号的电波，RLC电路呈现出较高的阻抗Z，相应的电流很小，电容两端的输出电压也很小，这种情况相当于只有载波频率为f₁的电磁波信号被输入电路接收并选择出来，而其他载波频率的信号不被输入电路所接收，所以收音机就能收到载波频率为f₁的电台信号。

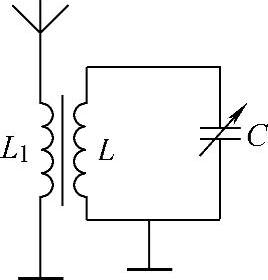
图2-54 收音机的输入电路