【例2-11】 列出图2-47所示电路的网孔电流方程。
解 设电路的网孔电流如图2-47所示,根据KVL可得
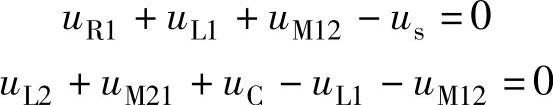
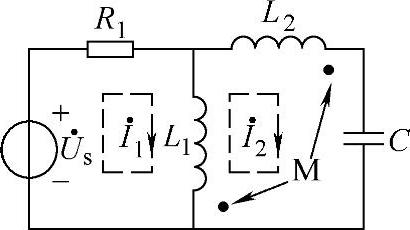
图2-47 例2-11图
写成相量形式为
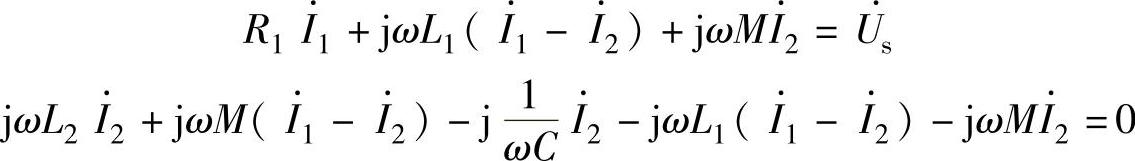
写成矩阵为
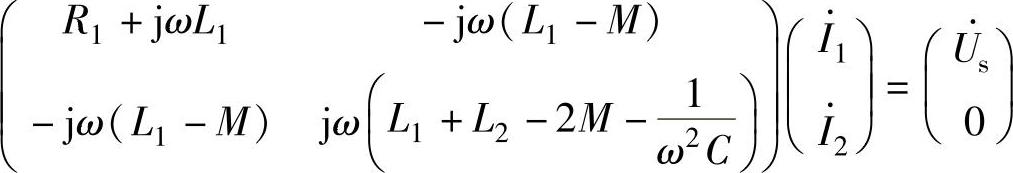
【例2-12】 求图2-48所示电路的输入阻抗Zi。
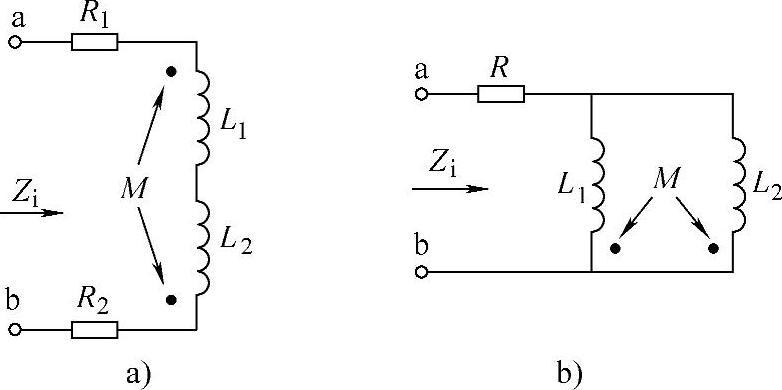
图2-48 例2-12图
解 本例用加压—求流法求解比较方便。在图2-48a所示的电路中,设外加的电压为uab,在该电压的激励下电路的电流为i,根据KVL可得
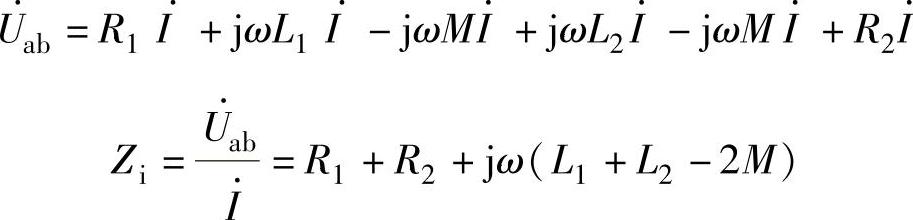
在图2-48b所示的电路中,设外加的电压为uab,在该电压的激励下电路的电流为i,根据KVL和节点电位法可得
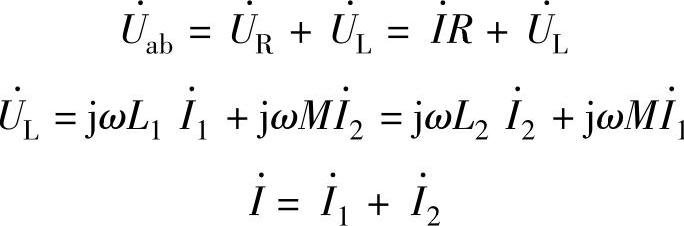
联立求解可得
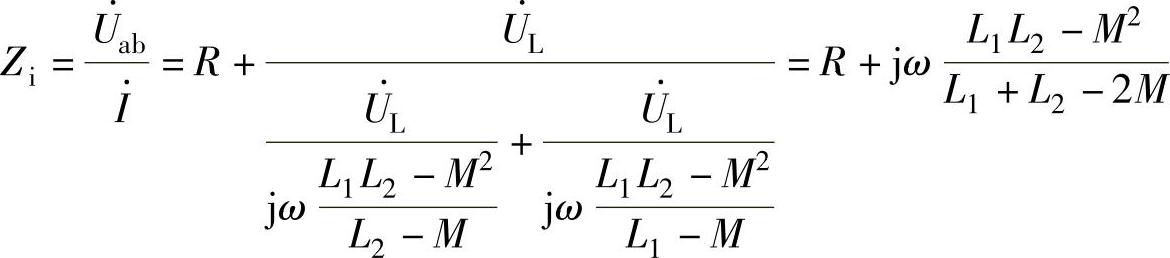
图2-48所示的电路等效于两个电感相串联和相并联的电路,上面的计算结果说明,两电感串联或并联的结果等效于一个自感系数为L的电感,等效电感的自感系数L不仅与两电感的自感系数L1和L2有关,还与互感系数M及同名端的排列有关。在图2-48a所示的电路中,两线圈的互感电压是反极性相串联的,在图2-48b所示的电路中,两互感电压是同极性相并联的。改变图2-48所示电路同名端的设置,可得两个自感线圈同极性相串联或反极性相并联的等效自感系数L=L1+L2+2M和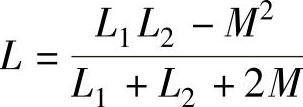 。综合上面的计算结果可得
。综合上面的计算结果可得
两自感线圈相串联的等效自感系数为
L=L1+L2±2M (2-65)
两自感线圈相并联的等效自感系数为

因为自感系数L是一个大于0的数,由式(2-65)可得两线圈相串联的最小互感系数为两线圈自感系数的算术平均值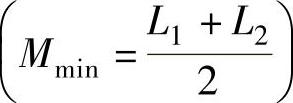 ,由式(2-66)可得两线圈相并联的最大互感系数为两线圈自感系数的几何平均值(
,由式(2-66)可得两线圈相并联的最大互感系数为两线圈自感系数的几何平均值(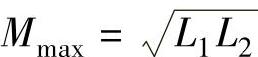 )。(https://www.xing528.com)
)。(https://www.xing528.com)
【例2-13】 图2-49a所示的电路为接收机输入电路的等效电路,为了实现电路的阻抗匹配,求自感分压系数与电容分压系数的关系。
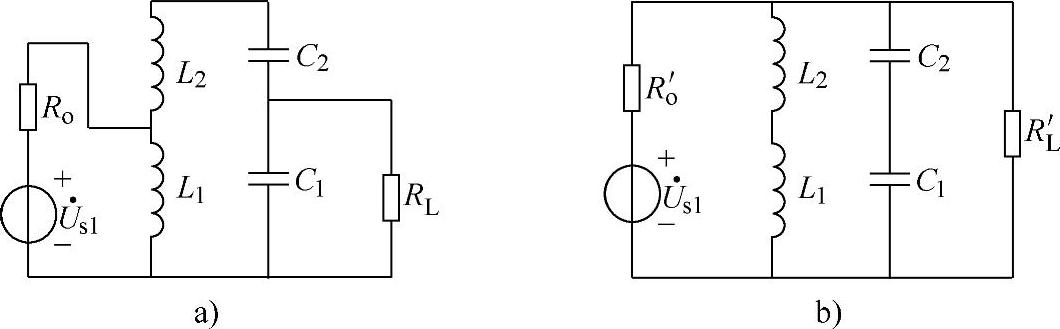
图2-49 例2-13图
解 当电源所带的负载等于电源的输出阻抗时,电路可实现阻抗匹配。在图2-49a所示的电路中,电源通过电感分压电路输出,负载电阻通过电容分压电路与电源的输出电压相连。设负载电阻通过电容分压电路后的等效阻抗为RL′,电源的输出阻抗Ro通过电感分压电路后的等效阻抗为Ro′,阻抗匹配的要求是Ro′=RL′,计算RL′和Ro′的电路如图2-46b所示。利用阻抗变换功率相等的特点可得电容分压阻抗变换的规律为
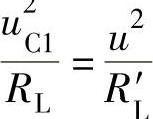
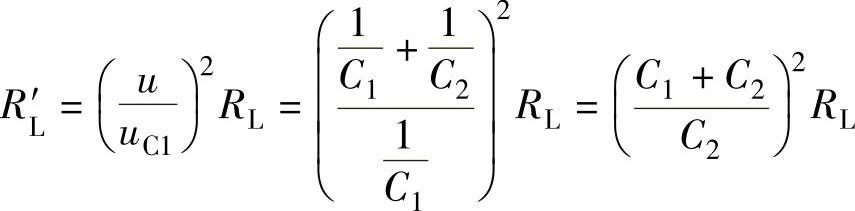
在两个电感线圈没有互感作用的前提下,利用阻抗变换功率相等的特点可得电感分压阻抗变换的规律为
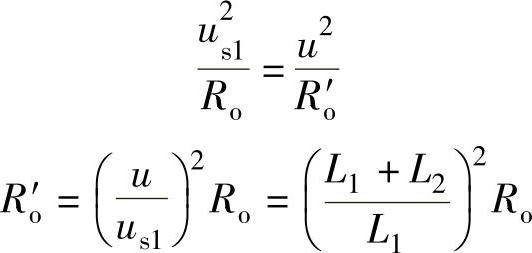
根据阻抗匹配的条件可得RL′和Ro′的关系为
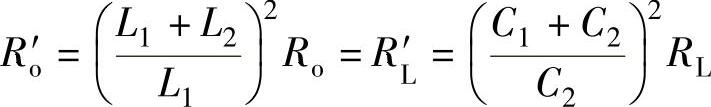
整理后可得自感分压系数与电容分压系数的关系为
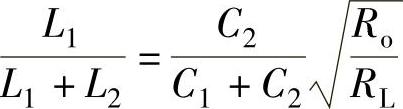
以上介绍的各种分析方法仅适用于正弦交流电量,在分析非正弦交流电量的问题时,应先利用高等数学介绍的傅里叶级数的概念,将非正弦信号展成不同频率的正弦信号,然后再利用叠加定理求解。
【例2-14】 如图2-50所示的电路中,已知R=0.5kΩ,C=50μF,ab端口的输入电压u(t)=(1+1.5cos200t)V,求各支路的电流i(t)、i1(t)和i2(t)。
解 因输入电压是直流电压和正弦交流电压的叠加,先将输入电压分解成直流电压和正弦交流电压,然后利用叠加定理求解。直流电压单独作用时各支路的电流为
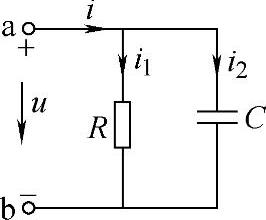
图2-50 例2-14图
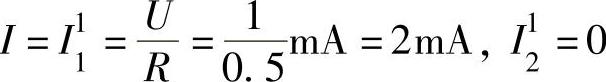
设交流电压的相量为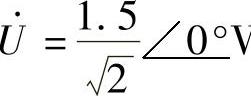 V,则交流电压单独作用时,各支路的电流为
V,则交流电压单独作用时,各支路的电流为
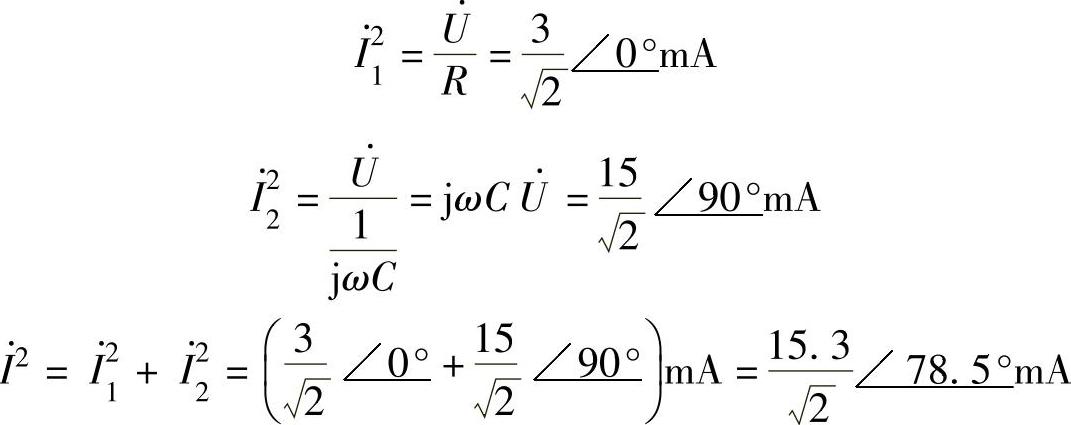
根据叠加定理可得各支路的电流为
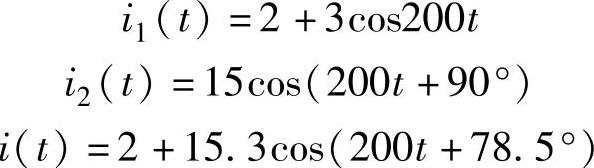
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




