互感和变压器：简介与应用

【例2-9】 求图2-40所示的电路电阻R₂两端的输出电压U_o。

解 图2-40中的L₁、L₂组成一个变压器，根据物理学课程的知识可知，变压器是利用磁耦合的原理来实现变压的。磁耦合的工作过程是：两个绕在一起的耦合线圈L₁和L₂，当线圈L₁中通有电流i₁时，i₁电流在线圈L₁上所产生的磁通将交链到线圈L₂上，并在线圈L₂上激发出感应电动势e₂₁。规定电流的参考方向与磁链的参考方向之间符合右螺旋法则，根据法拉第电磁感应定律可得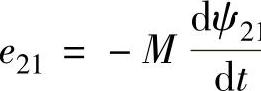1，式中的M称为线圈的互感系数，简称互感，它是由两线圈的材料和形状决定的。

两线圈磁耦合的作用不仅与两线圈的形状有关，还与两线圈的绕向有关。当两线圈的绕向相同时，互感磁通链和线圈的自感磁通链的方向相同，互感磁通链对自感磁通链起增助的作用；当两线圈的绕向相反时，互感磁通链和线圈的自感磁通链方向相反，互感磁通链对自感磁通链起削弱的作用。为了描述互感磁通链对自感磁通链增助和削弱的作用，采用同名端标记法，图2-40中的两个黑点即表示两互感线圈的同名端。

同名端的定义是，当一对施感电流i₁和i₂从同名端流入各自的线圈时，互感起增助的作用。设互感电压的方向如图2-41所示，根据上面同名端的定义可得图2-40所示电路的KVL公式为

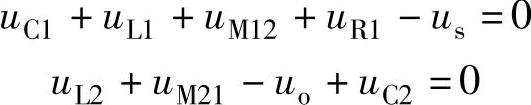
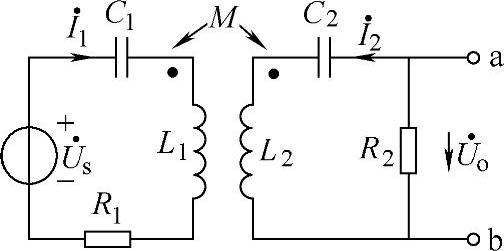
图2-40 例2-9图

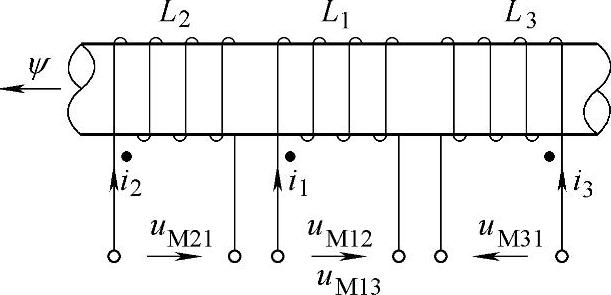
图2-41 互感电压的方向与同名端的关系

式中的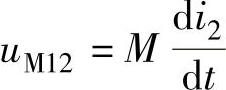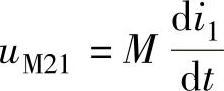，，将u_M、u_C、u_L等表达式写成相量形式并代入上面两式

可得

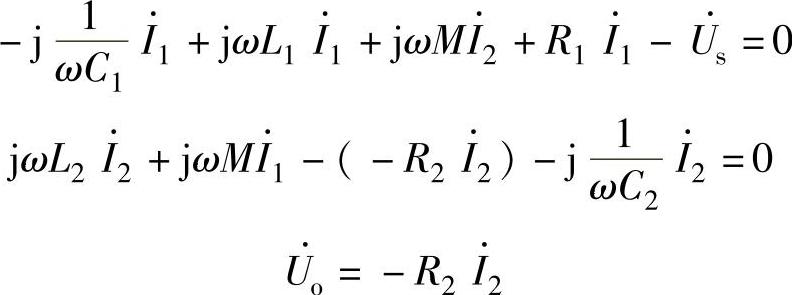
将上式写成矩阵为

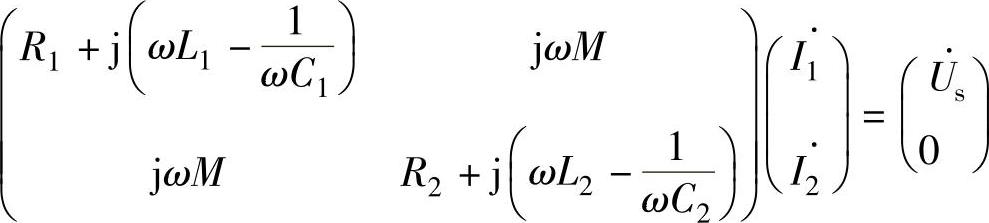
用MATLAB求解的程序为

该程序运行的结果为

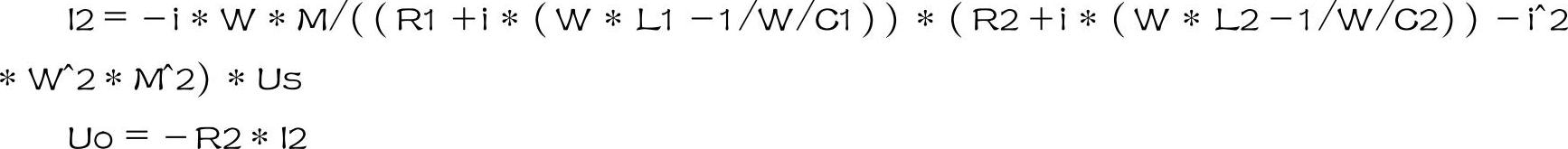
根据运行的结果可得输出电压的表达式为

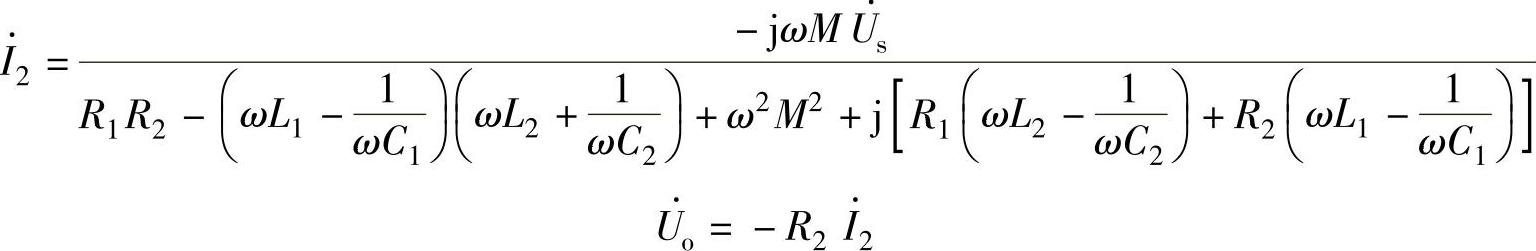
如果将同名端的标注改成如图2-42所示的形式，则KVL的表达式为(www.xing528.com)

u_C1+u_L1-u_M12+u_R1-u_s=0

u_L2-u_M21-u_o+u_C2=0

写成相量形式为

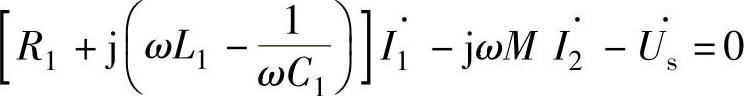
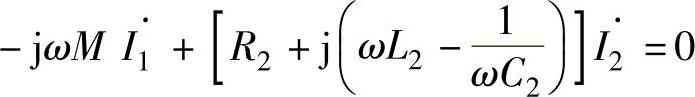
在图2-41所示的电路中，当铁心的磁导率为无穷大，磁通的外漏、线圈和铁心的损耗都可以忽略不计的情况下，图2-41电路所表示的器件为理想变压器。描述理想变压器性能的参数为变压器的变比n，变压器的符号和变比n的定义如图2-43所示。

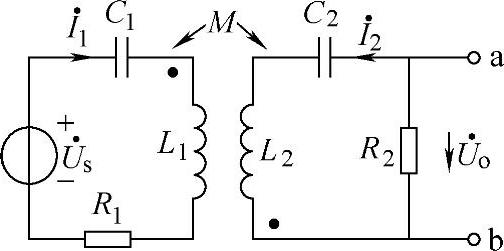
图2-42 例2-9同名端改动后的电路

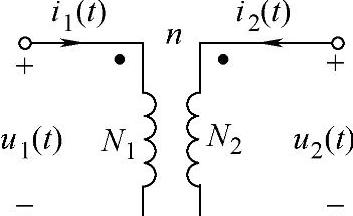
图2-43 理想变压器

在图2-43中，线圈N₁所在的电路称为变压器的一次线圈，线圈N₂所在的电路称为变压器的二次线圈。线圈两端电压的表达式为

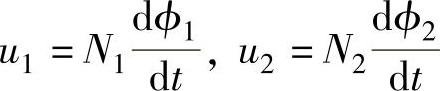
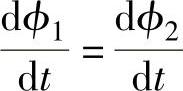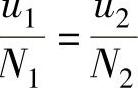在理想变压器的情况下，因，所以，即

式（2-62）说明，变压器变比n的定义为，变压器一次线圈的匝数N₁和二次线圈的匝数N₂之比。在图2-43中，因为外加的电源是接在变压器一次线圈所在的电路上，所以，变压器一次线圈所在的电路为外电源的负载。因为变压器二次线圈的输出电压需要带相应的负载，所以，变压器二次电路的输出端为电源的输出端。根据负载所消耗功率的表达式和电源输出功率的表达式可得

p₁=u₁i₁，p₂=-u₂i₂

在理想变压器的情况下，因为p₁=p₂，所以u₁/u₂=-i₂/i₁，即

变压器不仅在电路中可以实现变压的目的，还可以实现阻抗变换的目的。设变压器二次线圈所带的负载阻抗为Z_L，该阻抗在一次线圈上的等效值为Z′_L，在正弦稳态电路的前提下，根据相量形式的欧姆定律和式（2-63）可得

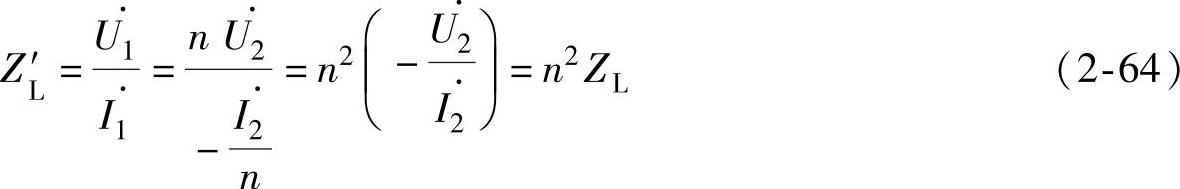
式（2-64）说明，变压器二次回路的阻抗在一次回路中的等效值为原阻抗的n²倍。