综合例题：正弦稳态电路分析方法

【例2-4】 如图2-25所示的电路，已知各电流表的读数为A₁=1A，A₂=2A，A₃=3A，求：

（1）电流表A的读数是多少？

（2）若A₁不变，角频率ω变为2ω，电流表A的读数又是多少？并画出相量图。

图2-25 例2-4图

解（1）该电路是一个R、L、C相并联的电路，电流表A₁、A₂、A₃的读数分别是各支路电流的有效值，电流表A的读数是总电流的有效值，将电路的电压和电流的参考方向设成关联的，由KCL得

为了进行相量的计算，必须先将、、的相量表达式写出来，要写出这三个相量的表达式，必须先选定基准相量。因为并联电路的电压相等，所以可选择电压为基准相量，设电路的电压相量为，根据R、L、C电路电流和电压的相量关系可得

将、、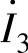的相量表达式代入式（2-56），根据相量运算的法则得

即电流表A的读数为1.4142A，

（2）当角频率由ω变为2ω时，感抗X_L0变成原来的2倍，即2X_L0，容抗由X_C0变成原来的1/2，即X_C0/2。此时，电流表A₂、A₃的读数分别为

则、、的相量表达式分别为

将上式的结果代入式（2-56），根据相量计算的法则得

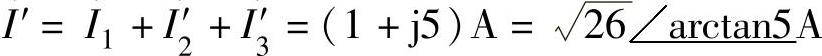
即电流表A的读数为8.01A，相量图如图2-26所示。

【例2-5】 如图2-27所示电路Z₁=（4+j10）Ω，Z₂=（8-j6）Ω，Z₃=j10Ω，U=60V，求各支路的电流并画出电压和电流的相量图。

解 该电路如果是直流电路的问题，相信大家很快就会写出计算电路总电阻的公式R=，然后写出计算总电流的公式，最后再用并联分流公式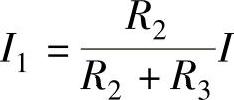求出各支路的电流，用串联分压公式求出各电阻两端的电压。

图2-26 例2-4相量图

图2-27 例2-5图

分析计算交流电路问题的思路与分析计算直流电路问题的思路完全相同，公式的形式也相同，所不同的地方仅仅是计算的方法。直流电路是代数运算，而交流电路则是相量或复数的运算。解题时，只要将上面根据直流电路分析法所列出的公式，改写成交流电路的相量形式或复数的形式即可。具体方法如下：

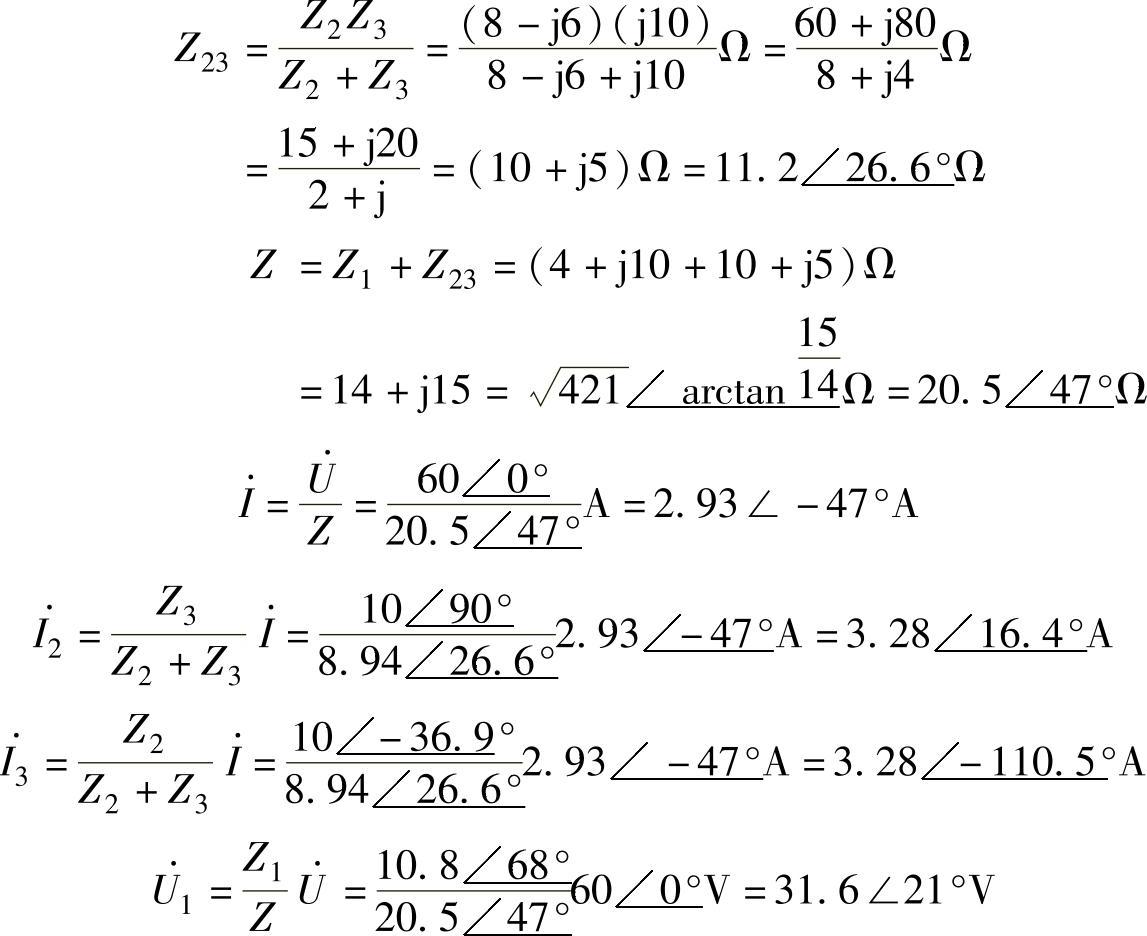
根据上面计算的结果选总电压相量为基准相量，可画出如图2-28所示的相量图。

上面的计算过程也可以用MATLAB编程进行，解题计算的程序为

该程序运行的结果为

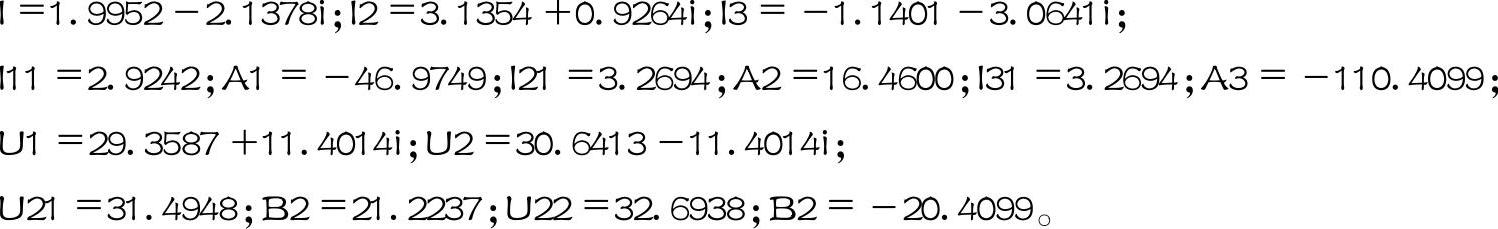
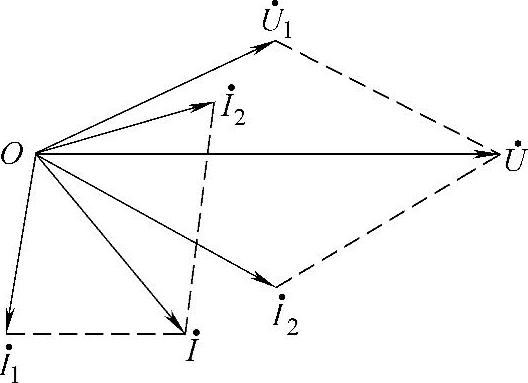
图2-28 例2-5相量图

用该程序所画的相量图如图2-29所示。

【例2-6】 在如图2-30所示的无源二端网络上加u（t）=2202cos（314t+20°）V的交流电压，设该网络的输入电流为i，求：

（1）该网络的有功功率、无功功率、视在功率。

（2）要将该网络的功率因数提高到0.9，需在电路中并接一个多大的电容C？画出相量图。

解 因为功率三角形、阻抗三角形、电压三角形在数值的关系上满足相似三角形的关系，所以阻抗三角形中的阻抗角等于功率三角形中的功率因数角，又等于电压三角形中总电流和总电压的夹角，选总电压为基准相量，总电流相量和总电压相量的夹角为

并上电容后的cosϕ=0.9，ϕ=±25.8°，且有功功率没有改变，流入网络的电流I也没有变，但并联电容后，因电容的分流作用，电路的总电流变了，电路的视在功率也变了，并上电容后，电路的视在功率S′为

与原来的相比减小了。并上电容后，电路总电流为

图2-29 用MATLAB画的相量图

图2-30 例2-6图

总电流的相量式为

根据相量运算的法则，可得电容所分电流的大小为

并接电容的容抗为

取容量小的电容并上更经济，则并联电容的容量为32μF。

上面的计算结果用MATLAB编程的解题程序为

该程序运行的结果为

相量图的画法除了前面介绍的平行四边形法则外，还可以用三角形法则来画，具体的画法与物理学中画矢量合成的方法一样。

以电压相量为基准相量，流入网络的电流相量滞后，流入电容C的电流相量超前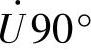，电路的总电流相量，用三角形法则画的相量图如图2-31所示，图中的虚线表示补偿电容用C₂时的相量图。(www.xing528.com)

由上面的计算过程可见，并上电容以后，网络消耗的有功功率没有变，但视在功率却减小了，对电源来说，相当于所带负载的伏安值减小了。电源可以将节省下来的伏安值用于其他的地方，使电源设备的容量得到充分的发挥，其效果与扩建电厂是等效的，这就是电网功率因数补偿的经济意义。

电网功率因数的补偿除了可充分发挥电源设备的利用率外，补偿后因电流减小了，输电线路的损耗也相应地减小，输电线路的效益也随着提高。

【例2-7】 如图2-32所示的独立电源全是同频正弦交流电量，试列出该电路矩阵形式的节点电压方程和回路电流方程。

图2-31 例2-6相量图

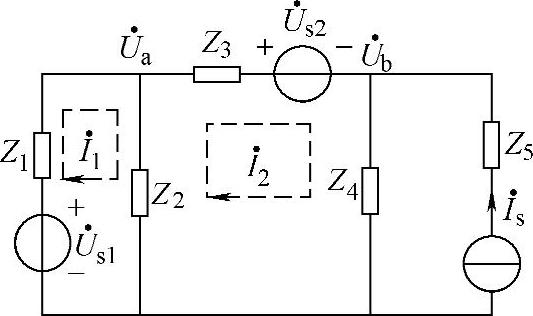
图2-32 例2-7图

解 因为节点电压方程和回路电流方程在直流电路和交流电路分析中的表示形式一样，所不同的仅仅是运算方法的差别，直流电路用的是代数运算，交流电路用的是复数或相量运算，根据这个思路，在解题时，完全可以将该问题看成是直流电路的问题来分析，具体写方程时再将方程写成相量的形式。

设电路各节点的电压如图2-32所示，由节点电压法得

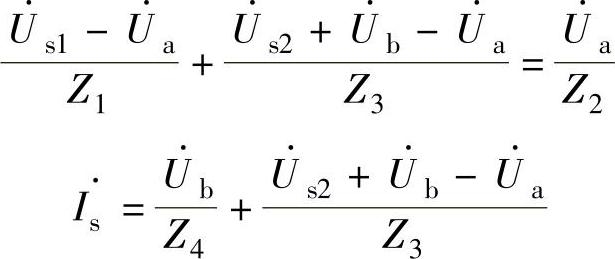
写成矩阵的形式为

设电路回路电流的参考方向如图2-32所示，由回路电流法得

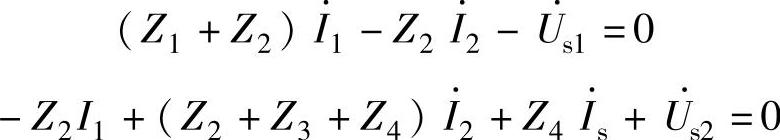
写成矩阵为

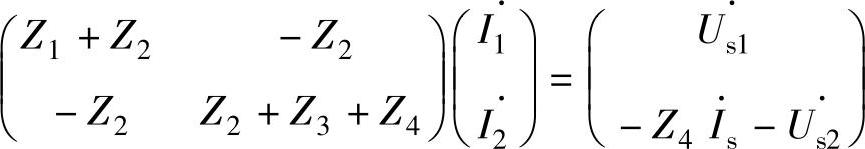
用MATLAB求解上述两个矩阵的程序为

【例2-8】 求图2-33所示电路点画线框内网络的输入阻抗，用戴维南定理求Z_L两端的电压。

解 网络输入阻抗的定义式是，根据电位的计算公式可得

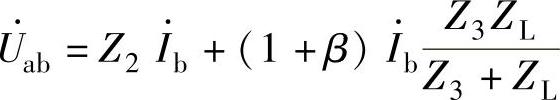
令

图2-33 例2-8图

则

又因为

所以，网络的输入阻抗Z_ab为

由式（2-58）解的结果可得到计算含有受控电源网络输入电阻的简单方法如下：

将受控电流源开路，但应保持Z_L′两端的电压不变，得到如图2-34所示的等效电路图。图2-34中的Z₂和Z_L′的两个阻抗是电流不相同的串联关系，为了利用串联电路的公式来计算总阻抗Z_a，必须将不相同的电流变换成相同的。

若在支路上计算Z，可将ZL′所在支路的电流缩小（1+β）倍，变成，电流缩小了（1+β）倍，为了保持Z_L′两端的电压不变，Z_L′就必须扩大（1+β）倍，由此可得

又因为Z_ab是Z₁和Z相并联的结果，所以

Z_ab=Z₁∥Z （2-60）

上式是式（2-58）的简写形式。

cb端开路后的等效电路如图2-35所示。由节点电位法可得

图2-34 计算输入阻抗的电路

图2-35 计算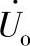的电路

计算内部带有受控电流源电路输出阻抗Z_o的方法可采用第1章介绍的加压-求流法，也可以采用开路-短路法。开路-短路法是根据的原理来计算有源二端网络的输出阻抗。上面的计算已经求出网络的开路电压，再计算出网络的短路电流即可求出网络的输出阻抗。计算短路电流的等效电路如图2-36所示。由图2-36可得短路电流为

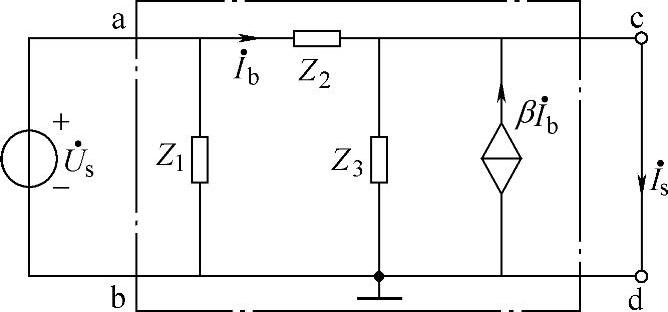
图2-36 计算短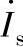路的电路

将开路电压和短路电流的表达式代入可计算出输出阻抗Z_o为

式（2-61）解的结果说明，计算含有受控电源网络输出阻抗的简单方法是：将受控电流源开路，电压源短路，因为计算Z_o是在（1+β）I_b的支路中进行的，该支路是大电流的电路，应将Z₂支路的电流I_b折算为（1+β）I_b支路的电流，所以，必须将Z₂所在支路的电流扩大为原来的（1+β）倍，电流扩大后，为了保持Z₂两端的电压不变，必须将阻抗Z₂缩小（1+β）倍，处理过程的等效电路图如图2-37所示，由图2-37即可得式（2-61）。

计算有受控电流源电路的输入阻抗和输出阻抗的过程，用Multisim仿真实验的结果如图2-38所示。

图2-37 计算输出阻抗的电路

图2-38 计算输入阻抗和输出阻抗仿真实验的结果

图2-38左边的电路是计算输入阻抗的电路，右边的电路是计算输出阻抗的电路，该电路受控电流源的β=100，将电路的各参数代入输入阻抗和输出阻抗的计算公式，可以验证理论计算结果的正确性。

根据戴维南定理可得该网络的等效电路如图2-39所示，由图2-39可得

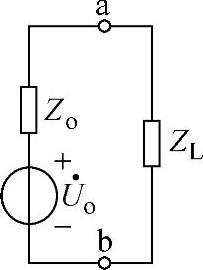
图2-39 例2-8等效电路