RLC串联电路功率关系探究

在2.3.2节中已知，纯电阻元件在电路中是负载，它将消耗电路的能量，将电能转换成其他形式的能量并对外做功，所做的功称为有功功率；纯电感和纯电容在电路中是储能元件，它们不消耗电路的能量，仅仅在电路上往复的与电源进行能量的交换，所交换能量的最大值称为无功功率，利用有功功率P=I²R和无功功率Q=I²X的关系式，可以讨论这些功率之间的关系。在式（2-49）的两端同乘I²得

I²Z=I²R+jI²（X_L-X_C）

S=P+jQ （2-52）

说明功率的运算关系等同于复数的运算关系，用复数表示三个功率之间关系的表达式称为复功率关系。

根据功率是标量的特征和复功率的关系式，也可以作出如图2-24所示的总功率、有功功率和无功功率的关系图。

图中的P=I²R为电路所消耗的有功功率，Q=I²X为电路的总无功功率，S=UI称为电路的视在功率。图2-24说明S、P、O数值之间的关系也构成一个三角形，该三角形称为功率三角形。由图2-24可见，视在功率S、有功功率P、无功功率Q三者数值之间的关系满足勾股定理，即

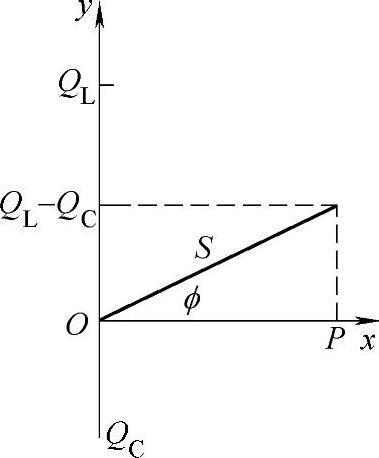
图2-24 功率三角形

有功功率P与视在功率S之间夹角的余弦称为电路的功率因数，即

功率因数是描述电源设备利用率的物理量，式中的ϕ称为功率因数角。(www.xing528.com)

由上面的讨论可知，功率三角形是一张反映视在功率、有功功率、无功功率数值之间关系的三角形，它描述了三个功率之间的数量关系。

在纯电阻电路中，因电流和电压同相，ϕ=0，cosϕ=1，P=S=IU；在纯电感或纯电容电路中，因电流和电压的相量正交，ϕ=90°，cosϕ=0，P=0；在一般情况下，电路中同时存在有R、L、C元件，电流和电压之间的夹角在-90°＜ϕ＜90°之间，电路的功率因数在0＜cosϕ＜1之间，电路消耗的有功功率为0＜P＜S。

由上面的讨论可知，视在功率S并不表示交流电路实际消耗的功率，它只是表示电源可能提供的最大功率或电路可能消耗的最大有功功率。为了与实际的有功功率相区别，视在功率的单位用伏安（V·A）或千伏安（kV·A）表示。

交流电源设备如交流发电机、变压器、交流稳压电源等，其额定电压U_N和额定电流I_N的乘积，指的就是这些设备的额定视在功率S_N

S_N=U_NI_N （2-55）

额定视在功率S_N又称额定容量，简称容量。它表明电源设备允许提供的最大有功功率，但不是实际输出的有功功率。这也是交流发电机、变压器、交流稳压电源等电源设备容量的计量单位用伏安，而不用瓦的原因。

一个电源实际输出的有功功率与电源所接负载的特性有关。当电源接的是纯电阻负载时，实际输出的有功功率等于电源的容量；当电源不是接纯电阻负载时，实际输出的有功功率将小于电源的容量。

电源接负载的目的是为了实现能量的转换。即通过负载将电场能量转化成其他形式的能量对外做功，输出有功功率。但电源所接的负载有许多像电动机那样的设备，这些设备主要是由各种线圈组成的，对电源来说是一个感性的负载。电源带这样的设备，因电流和电压不同相，功率因数将下降，电源设备的利用率将下降。要提高电源设备的利用率，必须提高电路的功率因数。

根据功率三角形可知，提高功率因数的方法是：采用适当的办法减小负载的电抗值，由阻抗三角形可知，采用性质相反的负载进行补偿就可实现减小负载的电抗值，增大功率因数的目的，这个过程称为功率因数的补偿。对于感性负载，可用容性负载进行功率因数的补偿；而对于容性负载，可用感性负载来进行功率因数的补偿。

前面介绍的电压三角形、阻抗三角形和功率三角形，虽然所表示的物理含义不同，但在几何数值的关系上是相似三角形，可以利用解相似三角形的办法进行相应物理量的数值计算。