纯电容元件的交流电路优化方案

1.纯电容元件的瞬时值伏安关系

电容元件是电路的重要元件之一，用途十分广泛。在电力系统中可用电容元件来提高电网的功率因数；在电子技术中将电容元件用于滤波、隔直、选频等。

根据物理学课程的知识可知，在两个金属极板的中间夹上绝缘材料就构成电容器。电容元件的交流电路如图2-18所示，图中的箭头表示电容元件两端的电压u（t）和电流i（t）的参考方向相关联。

设加在电容两端的电压为u（t）=U_mcosωt，根据电容器电容的定义式U=Q/C可得，当电压u（t）变化时，电容器上所储存的电荷也将发生变化。电荷有变化，说明有电流流过电容，根据电流的定义式可得

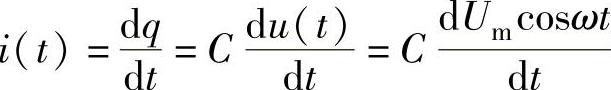
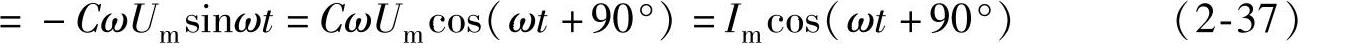
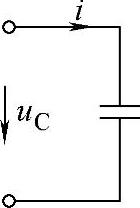
图2-18 纯电容电路

式（2-37）描述了流过电容电路的电流瞬时值与电容器两端电压瞬时值之间的关系，称为纯电容元件的瞬时值伏安关系。

式（2-37）说明电流i（t）与电压u（t）的变化率du（t）/（dt）成正比，即电压和电流的瞬时值之间与电感元件一样不满足欧姆定律的关系。式中的I_m=ωCU_m代表电流的最大值。将电流和电压的表达式写成相量形式为

式（2-38）的相量图如图2-19所示。由相量图和式（2-38）可得纯电容元件交流电路的电流与电压的关系是：

1）两者是同频率的正弦交流电量，电流和电压不同相，它们之间的相位关系是：电流超前电压90°，或者说电压滞后电流90°。

2）电流和电压的幅值或有效值的大小存在着以下关系：

I_Cm=U_mωC或I_C=UωC （2-39）

令

则式（2-39）可写成

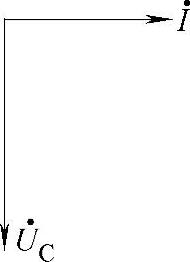
图2-19 纯电容电路的相量图

与描述纯电感电路电流和电压关系的思路一样，将X_C称为电容的电抗，简称容抗。若f的单位为Hz，C的单位为F（法拉），则X_C的单位是Ω。(www.xing528.com)

式（2-41）说明，容抗X_C与C和ω成反比。在频率ω一定时，电容C越大，X_C越小；当电容C一定时，频率ω越高，X_C越小，说明电容器对低频电流的阻抗作用大，对高频电流的阻抗作用小。

在直流电路中，因ω=0，X_C=∞，电容器两端虽有电压，但电路中的电流为零，相当于电容器开路，电容器的这一特性在电子电路中用来隔直流。

X_C与电容C及频率ω成反比的关系也可解释为：电容C越大，在同一频率下，电容器所容纳的电荷数就越多，电压变化时，流过电路的电流就越大，容抗就越小；当频率越高时，电容器的充放电进行得越快，在同样的电压下，单位时间内电荷的移动量就大，流过电容器的电流也大，容抗就小。

电容器上电流和电压的关系也可用相量运算的方法来讨论，为了与前面讨论的结果相比较，将流过电容器的电流当做已知的，设为i（t）=I_mcosωt，写成指数形式为I·=I_me^jωt。由电容器电容的定义式u（t）=q（t）/C=1/C∫i（t）dt可得

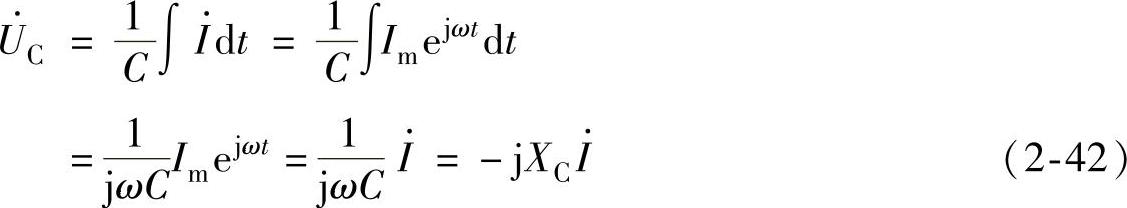
式（2-42）的结果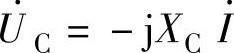与欧姆定律的形式相同，称为纯电容电路相量形式的欧姆定律。将式（2-32）中-j的表达式代入式（2-42）中，利用指数相乘的法则可得

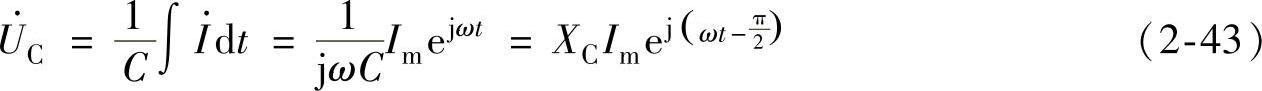
将式（2-43）与电流相量的表达式相比较可得，电压相量滞后电流相量90°。纯电容电路电流和电压的相位关系用Multisim软件进行仿真实验的结果如图2-20所示。

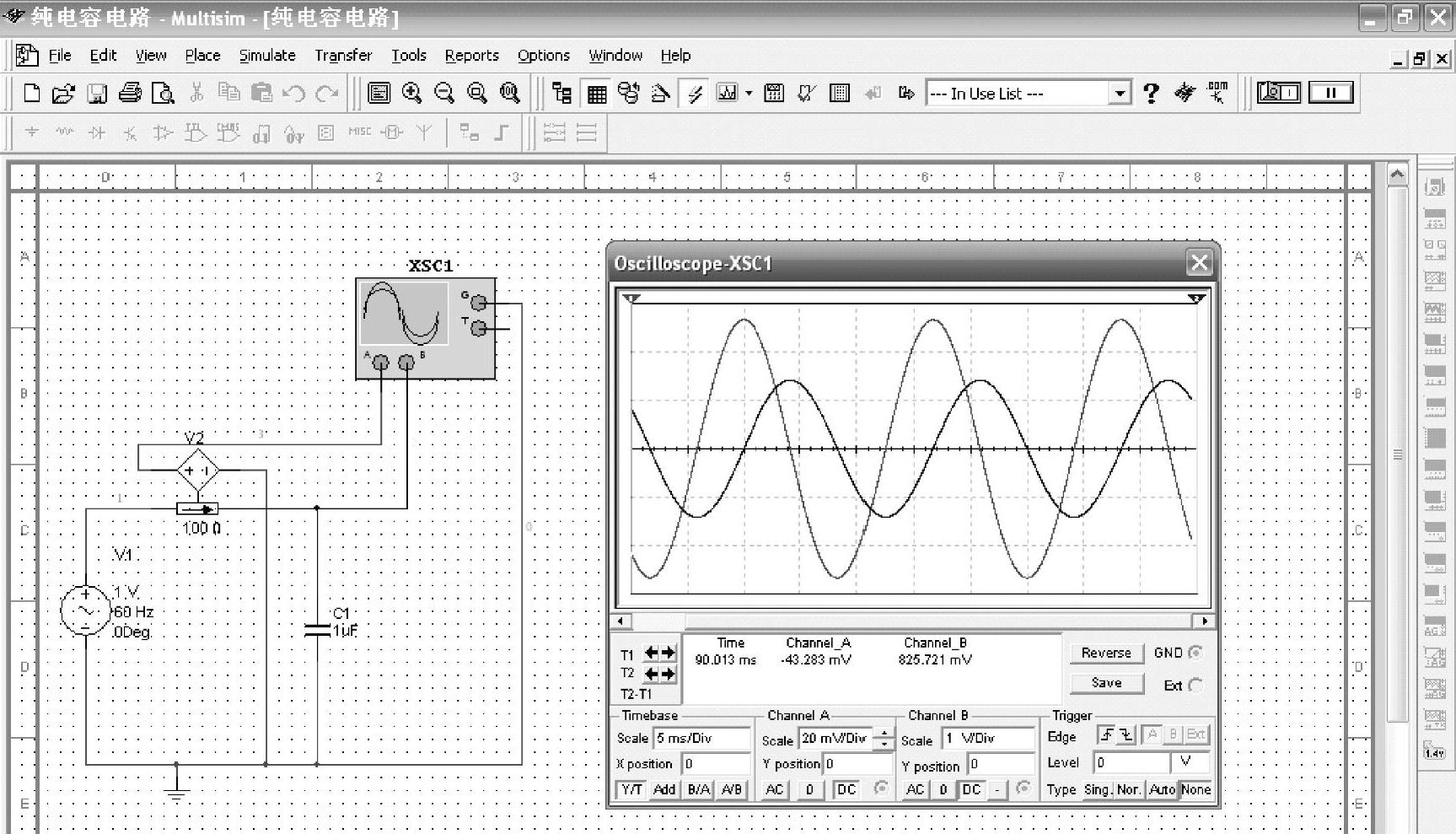
图2-20 纯电容电路电流和电压的相位关系

在图2-20中，幅度大的波形是电流信号的波形，幅度小的波形是电压信号的波形。在一个周期内，电压信号波形的极值点较电流信号波形的极值点先到达坐标原点，所以，电压滞后电流，滞后的相位为90°。

2.功率计算

与电感电路计算功率的方法相同，电容电路的瞬时功率p（t）为

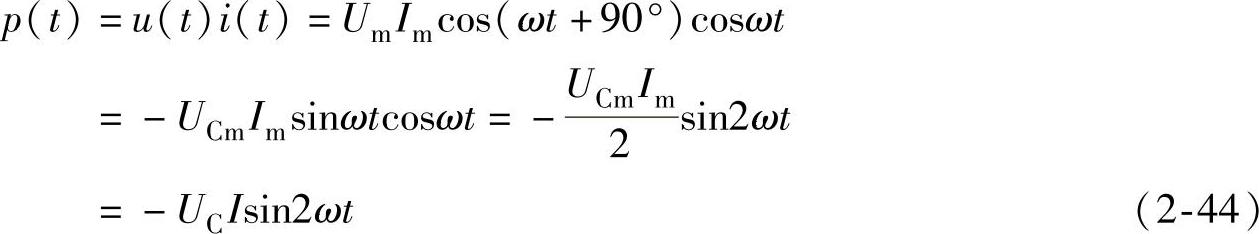
式（2-44）说明瞬时功率p（t）也是一个幅值为U_CI，并以2ω的角频率随时间作正弦规律变化的正弦量。当sin2ωt＜0时，瞬时功率p（t）＞0，电容在电路中是负载，电容从电源吸收电能，并将电能转换为电场能量储存在电容器的电场中。当sin2ωt＞0时，瞬时功率p（t）＜0，电容器在电路中是电源，电容器将向电源释放能量，将刚才储存的电能送还给电源。这种能量转换的过程也是可逆的。

由此可见，纯电容元件和纯电感元件一样在电路中并不消耗能量，而是和电源不断地进行能量的交换。这也是一个可逆的能量转换过程，平均功率P为0，计算无功功率的表达式为

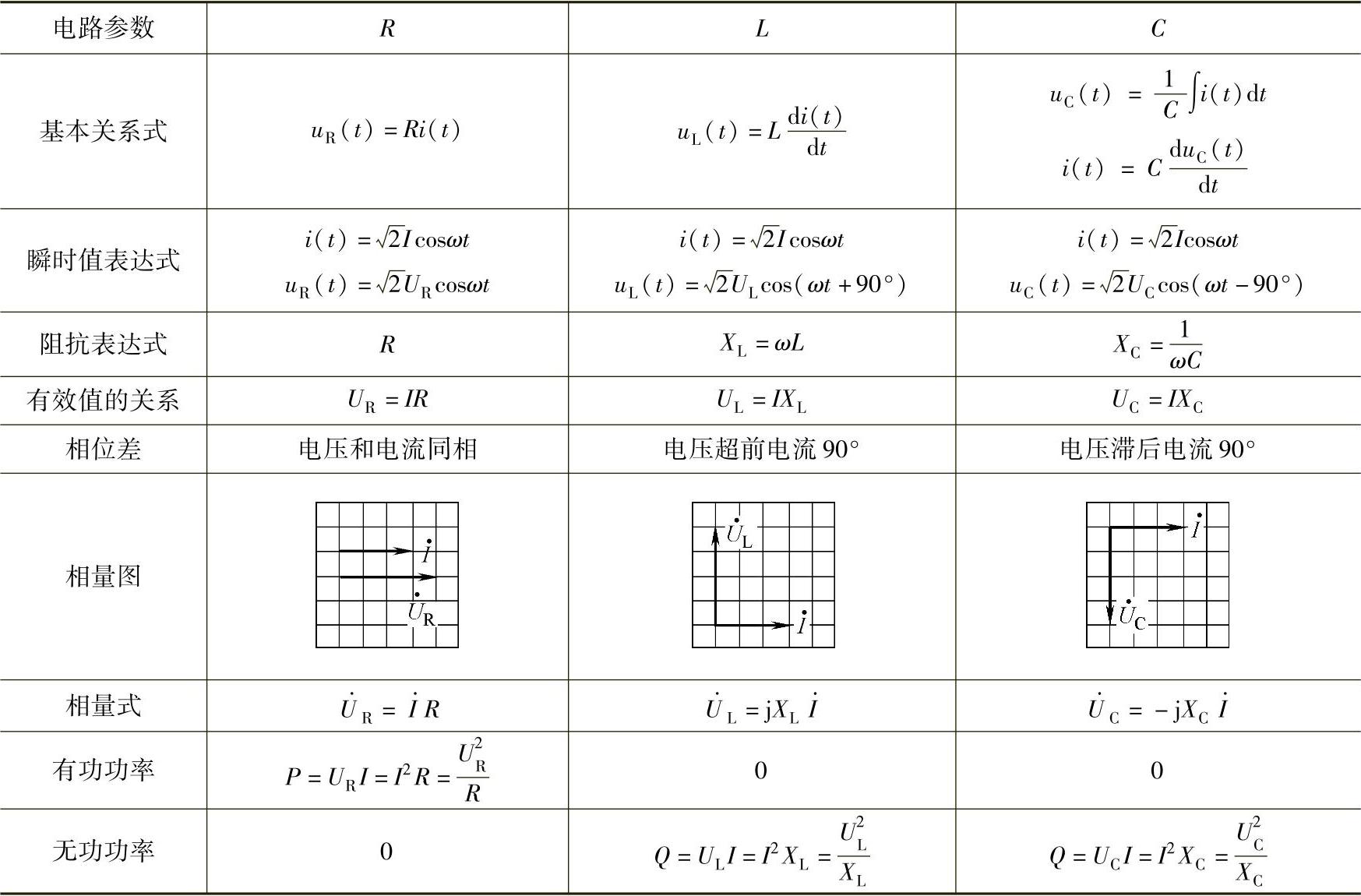
单一参数R、L、C各元件在交流电路中的电压、电流间的关系是分析计算交流电路的重要基础，为了帮助记忆，将它们在交流电路中的表示方法和相互关系列于表2-2中。

表2-2 R、L、C电路电流和电压之间的关系