纯电感元件的交流电路设计优化

1.纯电感元件

在物理课程中，将由导线绕制成的N匝螺线管称为电感线圈。线圈内部没有铁磁物质的称为线性电感线圈，如图2-14a所示。

当线圈中有电流i流过时，线圈内部就会产生磁链ψ，规定电流i的参考方向与磁链ψ的参考方向之间符合如图2-14a所示的右螺旋定则。线性电感线圈的磁链ψ与线圈中电流i成正比的关系，其比值L称为自感系数，简称电感，它表示单位电流所产生的磁链数。即

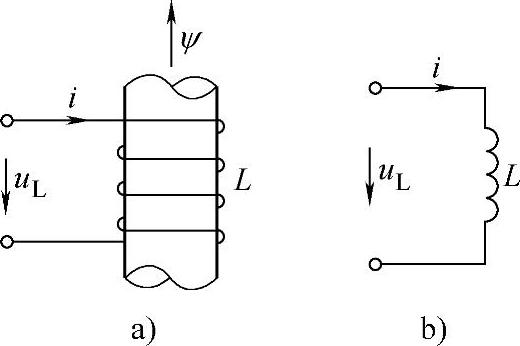
图2-14 纯电感电路

线性电感线圈的L是一个与i、ψ无关的常数。若线圈中含有铁磁物质，则L与i、ψ有关，不是常数。由物理学知识可知，线圈的电感与线圈的形状、几何尺寸、匝数以及周围物质的导磁性质有关，即

式中，l为密绕长线圈的长度（单位：m）；S为横截面（单位：m²）；N为匝数；μ为介质的磁导率。在线性电感线圈的电阻很小，可以忽略不计的情况下，线性电感线圈成为理想的电感元件，称为纯电感元件，它在电路中的符号如图2-14b所示。

2.自感电动势

当纯电感元件中通入随时间而变化的交流电流i（t）时，线圈的磁链也将随着电流的变化而变化，根据电磁感应定律，变化的磁链将在线圈中激励出自感电动势e_L（t）。自感电动势的大小与磁链的变化率成正比，自感电动势的方向由楞次定律来判定。楞次定律指出，感应电流的方向总是阻碍原磁链的变化。

规定自感电动势e_L（t）的参考方向与磁链的参考方向之间符合如图2-14a所示的右螺旋定则，由法拉第电磁感应定律得

式（2-23）说明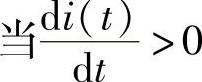，时，e_L（t）＜0，实际的方向与参考方向相反；当

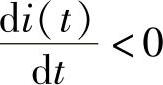时，e_L（t）＞0，实际的方向与参考方向相同。

3.纯电感元件的瞬时值伏安关系

将纯电感元件接入正弦交流电路中，根据电源电动势和电源两端电压的实际方向为非关联的特征，可得电感两端电压u_L（t）的表达式为

式（2-24）描述了电感线圈两端电压的瞬时值与电流的瞬时值之间所遵循的关系，称为纯电感元件的瞬时值伏安关系。

式（2-24）说明u_L（t）与

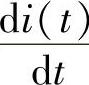成正比，电流变化得越快，线圈的自感电势越大，相应的端电压也越高。当电流是不随时间而变化的直流电时，感应电势e_L（t）等于零，线圈两端的电压u_L（t）也等于零。说明电感线圈在直流电路中仅相当于一根短接线。

若在电感线圈中通入i（t）=I_mcosωt的正弦交流电流，根据式（2-24）可求出电感线圈两端的电压u_L（t）为

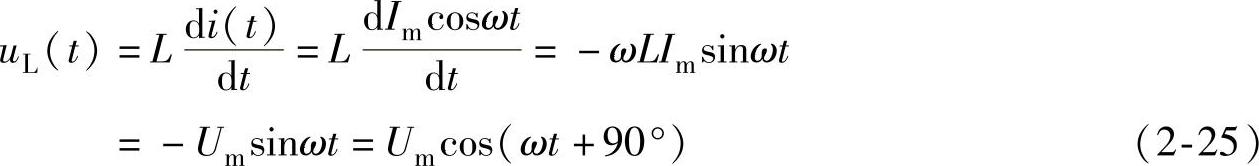
式（2-25）中的U_m=ωLI_m，表示电压的最大值。将电流和电压的表达式写成相量式

式（2-26）的相量图如图2-15所示。由相量图和式（2-26）可得电感元件交流电路的电压与电流之间的关系是：

1）两者为同频率的正弦交流电量，但两者不同相，它们之间的相位关系是：电压超前电流90°，或者说电流滞后电压90°。

2）电压和电流在幅值或有效值的大小上存在着以下关系：

U_Lm=I_mωL或U_L=IωL （2-27）

令

X_L=ωL=2πfL （2-28）

图2-15 纯电感电路的相量图

则式（2-27）可写成

U_L=IX_L （2-29）

式（2-29）的形式与描述纯电阻电路电流和电压之间关系的欧姆定律相同。引用欧姆定律的概念，可将X_L称为电感的电抗，简称感抗。若f的单位用Hz，L的单位用亨利（H），则X_L的单位是Ω。(www.xing528.com)

由式（2-28）可得，感抗X_L与L和ω成正比的关系。在频率ω一定时，电感L越大，X_L也越大，说明自感电动势对电流的反抗作用就大；当电感L一定时，频率ω越高，X_L也越大，说明电感线圈对高频电流的阻抗作用很大。在直流电路中，因ω=0，X_L=0，所以线圈两端的电压也为零。表明电感元件对直流电无阻碍作用，可视为短路。

利用电感线圈的这一特性可以制作各种形式的滤波器，滤掉电路中的高频干扰信号。例如，计算机实验室中用的电源滤波器内部就有一个滤波电感，该电感就是利用电感通直流、阻交流的特性来阻止高频电流的通过，将电网上的高频干扰信号滤掉。

当电路中电压一定时，X_L越大，电路的电流越小。所以，感抗X_L是表示电感对电流阻碍作用大小的物理量，这种阻碍作用和电阻元件对电流的阻碍作用相类似，但性质不同。

电阻R是由电荷定向运动与导体分子之间碰撞摩擦引起的，而电感中的阻碍作用则是感电动势反抗电流的变化作用而引起的。在电阻电路中，电流和电压瞬时关系的欧姆定律为u_R（t）=Ri（t），而在电感电路中这种关系不满足，电感电路瞬时值的伏安关系是u_L（t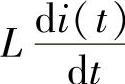）=，不满足欧姆定律的形式。但电感电路的有效值或最大值与感抗的数值关系仍满足欧姆定律的形式，即

电感线圈电流和电压的关系也可以用相量运算的方法来讨论，将流过电感线圈中的电流i（t）=I_mcosωt写成指数形式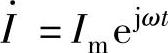。由式（2-24）可得

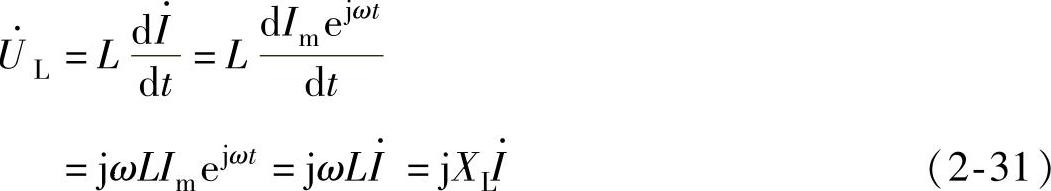
式（2-31）的结果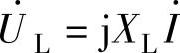与欧姆定律的形式相同，称为电感电路相量形式的欧姆定律。

为了讨论电压相量和电流相量之间的相位关系，我们来考察一个模等于1的单位相量。对于模等于1的单位相量，其端点运动的轨迹在复平面上是一个半径为1的单位圆，如图2-16所示。单位圆上a、b、c、d四个点复数的指数式为

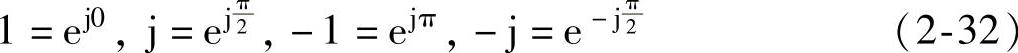
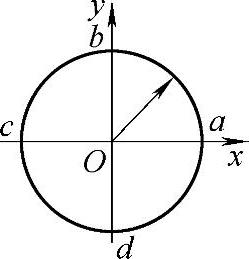
图2-16 单位相量图

将式（2-32）中j的表达式代入式（2-31）中，利用指数相乘的运算法则可得

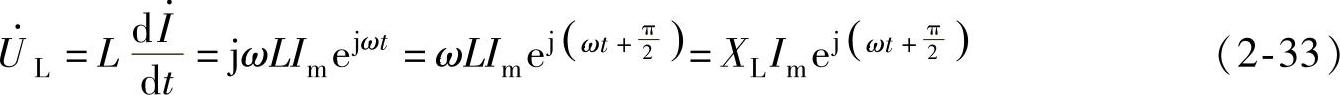
式（2-33）与电流相量的表达式相比较可得，电压相量超前电流相量90°。从式（2-33）还可看出，对相量进行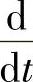的运算，相当于将原相量的模扩大ω倍的同时，将原相量沿逆时针方向转90°。根据这一特性，可将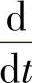看成相量的旋转算符，它每作用于相量一次，就将该相量沿逆时针方向转90°的同时，将相量的模扩大ω倍。利用这种运算法则来记忆电感电路电流和电压之间超前和滞后的关系非常简便，只要记住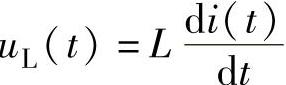的关系式和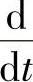的旋转特性，就记住了电感电路电压超前电流90°的关系。

纯电感电路电流和电压的相位关系也可以用Multisim软件来仿真，仿真实验的结果如图2-17所示。

在图2-17中，幅度大的波形是电流信号的波形，幅度小的波形是电压信号的波形。在一个周期内，电流信号波形的极值点较电压信号波形的极值点先到达坐标原点，所以电流滞后电压，滞后的相位为90°。

4.功率计算

（1）瞬时功率

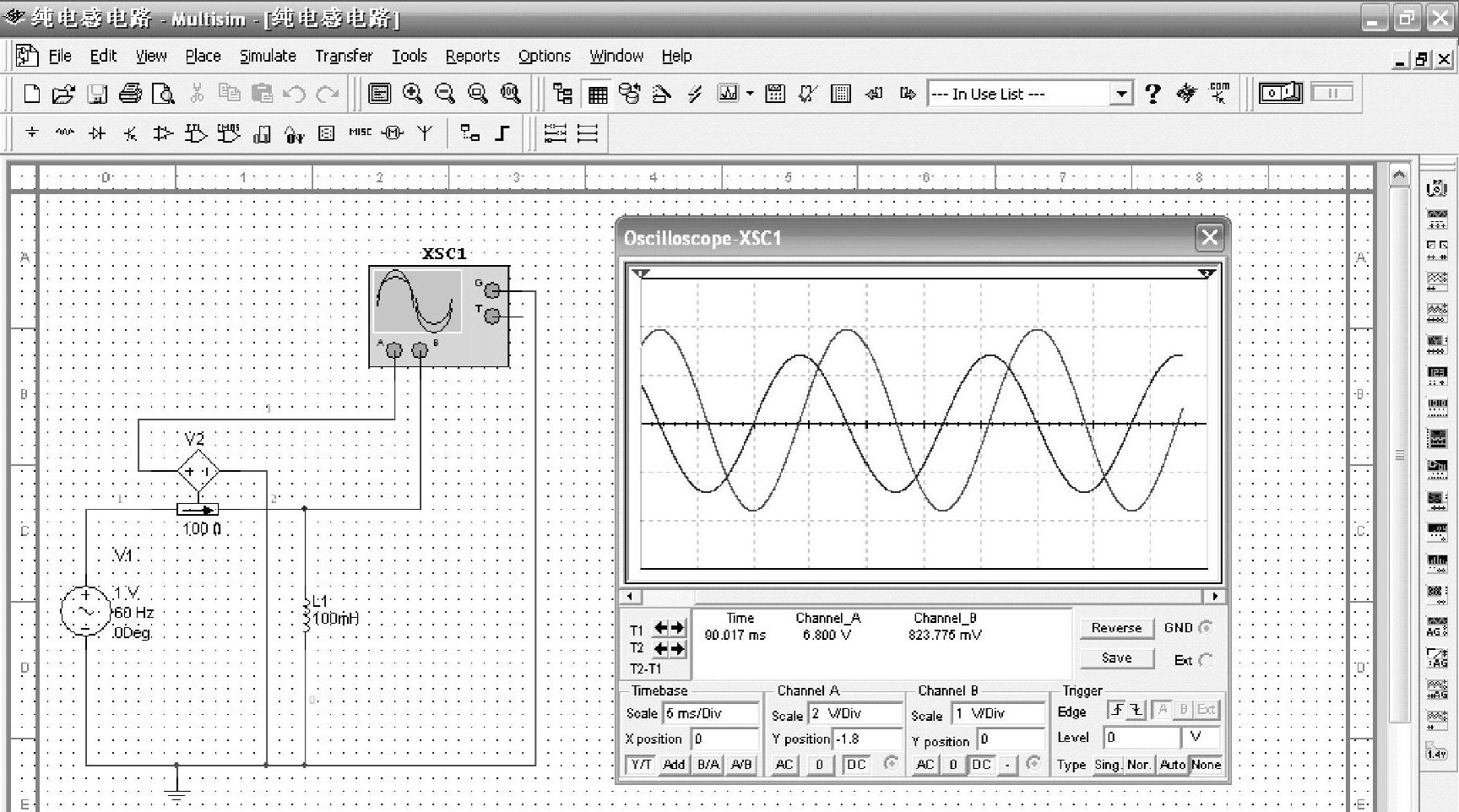
图2-17 纯电感电路电流和电压的相位关系

设u_L（t）和i_L（t）的参考方向相关联，根据p（t）的表达式可得电感电路的瞬时功率表达式为

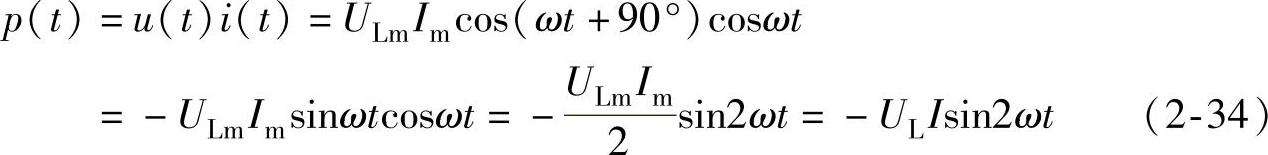
式（2-34）说明，纯电感元件的瞬时功率p（t）是一个幅值为U_LI，并以2ω的角频率随时间作正弦规律变化的正弦交流电量。当sin2ωt＜0时，瞬时功率p（t）＞0，电感在电路中是负载，电感从电源中吸收电功率，并将电能转换为磁场能量储存在线圈的磁场中。当sin2ωt＞0时，瞬时功率p（t）＜0，电感在电路中是电源，电感将向电源释放能量，将刚才储存的磁能转换为电能送还给电源。这种工作的过程说明，纯电感元件在电路中并不消耗能量，而是与电源不断地进行能量的交换，这是一个可逆的能量转换过程。

（2）平均功率

在纯电阻电路中平均功率是瞬时功率在一个周期内的平均值，根据平均功率的定义可求得纯电感电路的平均功率为

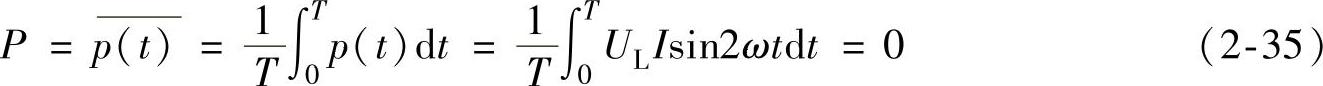
由式（2-35）可见，电感元件在电路中不消耗功率，不对外做功，有功功率P等于0。

（3）无功功率

电感元件在电路中虽然不消耗能量，但随着i（t）的变化将与电源不断地进行能量的交换。为了描述这种往复交换的能量规模，引入了无功功率的概念。

无功功率指的是储能元件与电源之间往复交换的最大电功率值。为了区别耗能元件的有功功率和储能元件的无功功率，用大写字母Q来表示无功功率。

因为sin2ωt=1时，瞬时功率p（t）有最大值U_LI，所以计算无功功率的表达式为

式（2-36）说明，计算无功功率的公式在形式上与计算有功功率的公式相似，差别仅在感抗和电阻上。在国际单位制中，无功功率的单位用乏（var）或千乏（kvar）来计量。