如何计算输入电阻？

电路（通常也称为网络或系统）的一个端口是它向外引出的一对端子，这对端子可以与外部电源或其他电路相连接。将KCL应用于端口可得：从端口的一个端子流入的电流一定等于从另一个端子流出的电流。这种具有向外引出一对端子的电路称为二端网络，常用图1-28所示的方框来表示。

如果一个端口内部仅含电阻，应用上面介绍的方法可以求出该网络内部的等效电阻。该电阻对外电路而言相当于一个跨接在端子1和2上的电阻R，也就是从端子1和2往网络内部看的电阻，该电阻称为网络的输入电阻，用符号r_i来表示。

图1-28 二端网络示意图

如果该网络内部除了含有电阻外，还含有受控电源（受控电压源或受控电流源），但没有任何独立的电源（电压源或电流源），理论上可以证明，不论该网络内部电路如何复杂，其外特性一定满足欧姆定律，即

式中，r_i为网络的输入阻抗（在直流电的情况下，输入阻抗即为输入电阻）；u为加在端口上的外电压；i为流入端口的电流。因为加在端口上的外电压和流入端口的电流不仅仅局限于直流电，所以用小写的字母来表示。

式（1-56）告诉我们，求一个网络的输入电阻r_i，除了用前面介绍的方法外，还可以通过以下方法来求解：首先在端口处外加一个输入电压u，然后测量在该电压的激励下，端口的输入电流i，最后利用欧姆定律求出网络的输入电阻，该方法称为加压-求流法。实验课上就是用这种方法来测量电路的输入电阻。下面给出一个用式（1-56）求电路输入电阻的例子。

【例1-8】 求图1-29所示电路端子a、b的输入电阻R_ab。已知各电阻的阻值相等，均为R。

解 求解这个问题若使用前面介绍的方法，将非常麻烦，几乎不可能求解。若利用求电路输入阻抗的式（1-56）将是非常简单。具体求解的思路是：

假设在电路a、b输入端子上加电压U_ab，在该电压的激励下，流入输入端子a的电流为I，根据电路对称的性质，ac支路的电流为I/3，cd支路的电流为I/6，db支路的电流为I/3，如图1-30所示。利用KVL列出U_ab和I的关系式，即可求出输入电阻R_ab。(www.xing528.com)

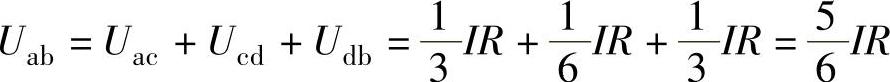
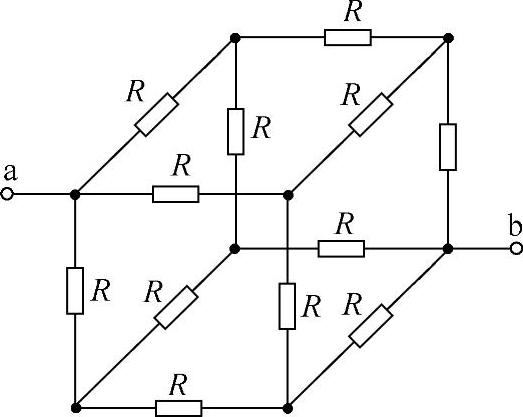
图1-29 例1-8电路图

图1-30 加输入电流标注后的电路图

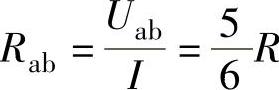
用Multisim软件仿真测试的结果如图1-31所示。

图1-31 例1-8用Multisim软件仿真测试的结果

图1-31中万用表面板上的数据与理论计算的结果相吻合。