支路电流法：求解复杂电路的关键

支路电流法是以支路电流为未知量，根据基尔霍夫定律列方程式，然后求出各支路电流的分析法。下面以图1-15所示的电路为例，说明支路电流法的内容和解题步骤。

图1-15的电路共有两个节点（a、c），三条支路（abc、ac、adc），三个回路（abca、adca、abcda），两个网孔（abca、adca），应用支路电流法可以很方便地求出三条支路的电流I₁、I₂和I₃。解题的步骤是：

1）设三条支路的电流分别为I₁、I₂和I₃，在图中标出三条支路电流的参考方向。在分析有n条支路的电路问题时，应设n个支路电流为未知量。

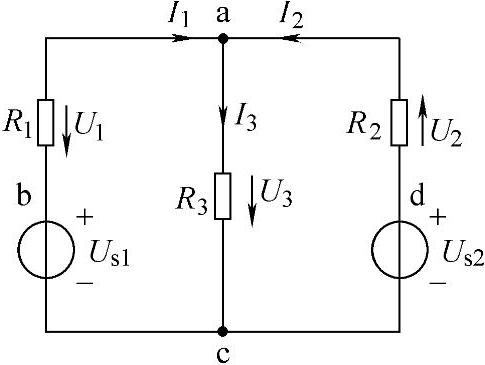
图1-15 应用支路电流法求解的电路

2）根据KCL对节点a和c分别列节点电流方程

节点a I₁+I₂=I₃ （1-30）

节点c I₃=I₁+I₂ （1-31）

由式（1-30）和式（1-31）可知，两个方程是一样的。说明两个节点，只能列一个独立的节点电流方程。当电路有三个节点时，可以证明，独立的节点电流方程只有两个；对于有N个节点的电路，独立的节点电流方程只有N-1个，另一个可由这N-1个方程联立求得。

在数学课程中已知，要求三个支路电流，必须有三个方程式，两个节点只能列一个独立的方程式，另外两个方程式可利用KVL列出。

3）在电路中标出各元件两端电压的参考方向，选择合适的回路，设定环绕方向，列KVL方程式。电路中有几个回路，就可以列几个KVL方程式。

对acba回路，设环绕的方向也是acba，KVL的方程为

U₃-U_s1-U₁=0 （1-32）

即 I₃R₃-U_s1-（-I₁R₁）=0

注意，电路中，R₁电阻上电流和电压的参考方向设为非关联，在写欧姆定律时，IR表达式前应加负号（上式括号内的乘积项）。为了解题的方便，一般不提倡将电阻R上电流和电压的参考方向设置成这种形式。

对adca回路，设环绕的方向也是adca，KVL方程为

-U₂+U_s2-U₃=0 （1-33）

即 -I₂R₂+U_s2-I₃R₃=0

对adcba回路，设环绕的方向也是adcba，KVL方程为

-U₂+U_s2-U_s1-U₁=0 （1-34）

即 -I₂R₂+U_s2-U_s1-（-I₁R₁）=0

显然，式（1-34）可由式（1-32）和式（1-33）相加求得，所以，它也不是独立的方程。一般在平面电路内，可选网孔作为回路，列网孔KVL方程，以保证方程的独立性。

所谓平面电路，指的是将电路画成一个平面图时，不出现任何交叉支路的电路。

当电路的支路数为M，节点数为N时，应用KVL可列出独立的方程数为L=M-（N-1）。

在R₁、R₂、R₃、U_s1和U_s2已知的情况下，联立解方程组，即可求出三个支路电流I₁、I₂和I₃。

【例1-4】设在图1-15所示的电路中R₁=1Ω，R₂=2Ω，R₃=3Ω，U_s1=3V，U_s2=1V。求：各支路电流I₁、I₂和I₃。

解 根据图中所标的参考方向，选节点a和回路acba、adca列方程，利用基尔霍夫定律可得

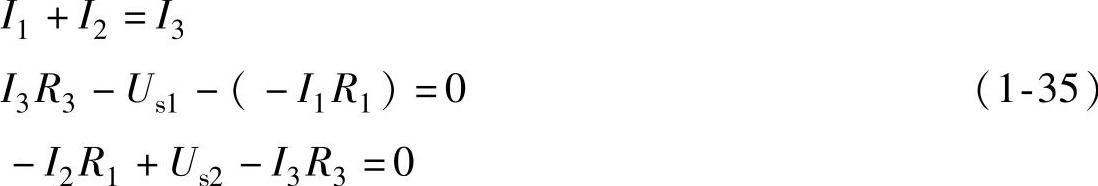
将上面的方程组整理成线性方程组的标准形式

将上面的线性方程组写成矩阵形式(www.xing528.com)

用MATLAB软件求解计算的程序为

该程序运行的结果如下：

上式说明I₁=1.0909，I₂=-0.4545，I₃=0.6364。

解的结果是I₁和I₃为正，说明这两个量的实际方向和参考方向相一致，I₂为负，说明这个量的实际方向和参考方向相反。解完之后，可将结果代入未选用过的回路，来验证结果的正确性。

上述解的结果也可以用Multisim软件来仿真，测试的结果如图1-16所示。

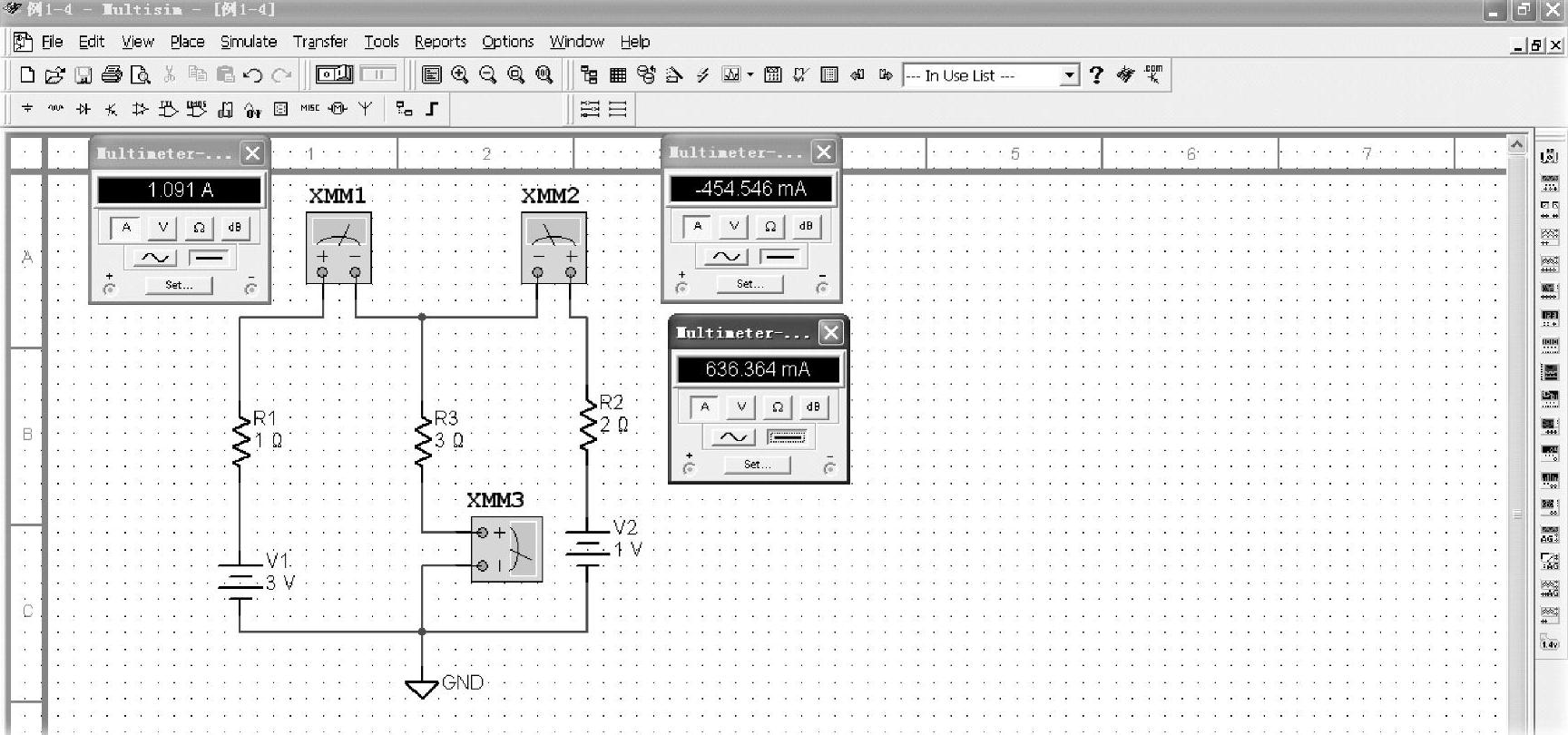
图1-16 例1-4用Multisim软件仿真测试的结果

图1-16中万用表面板上的数据与理论计算的结果相吻合。

【例1-5】求图1-17所示的电路中电阻R₃上的电流I₃。已知R₁=1Ω，R₂=2Ω，R₃=3Ω，U_s1=5V，U_s=5I₁。

解 图1-17所示电路的形式与图1-15的电路相似，差别仅在于将图1-15所示电路中的电压源U_s2变成了受控电压源U_s。所谓的受控电压源就是输出电压U_s的大小受外界输入信号控制的电压源。在本题中受控电压源的输出电压U_s=AI₁=5I₁，说明该受控电压源的输出电压受电流I₁的控制，输出电压的大小等于I₁电流的A倍，知道这些概念后，即可用基尔霍夫定律求解。

根据图中所标的参考方向，选节点a和回路acba、adca来列方程，利用基尔霍夫定律可得

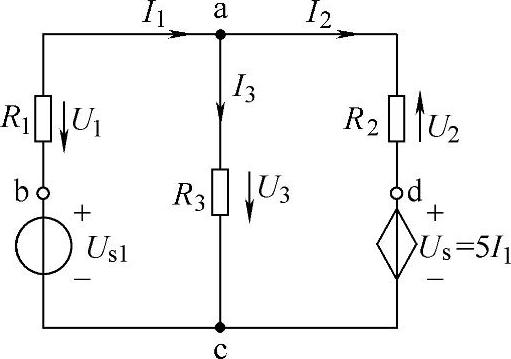
图1-17 例1-5电路图

将式（1-38）整理成矩阵为

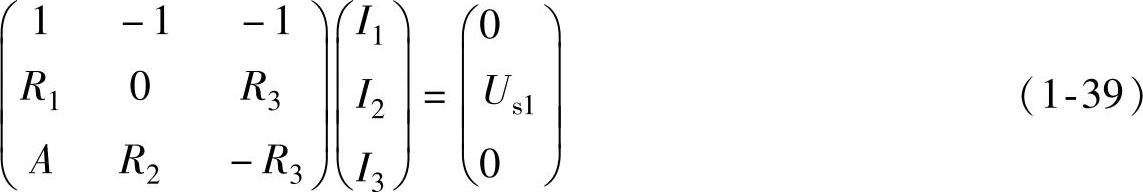
用MATLAB求解的程序为

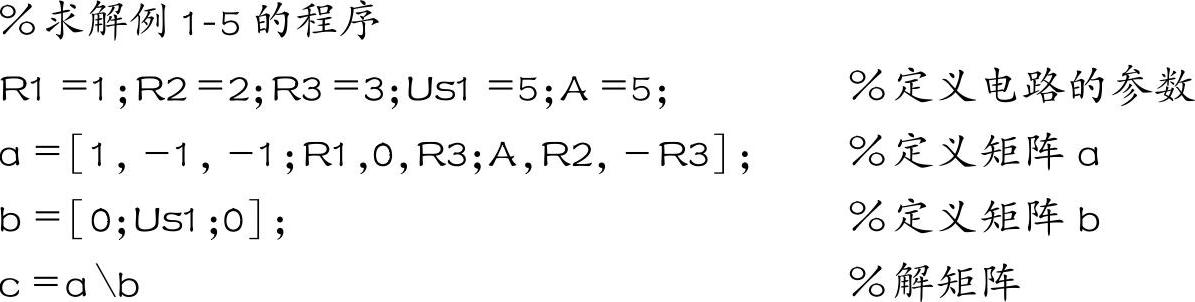
运行的结果为

根据MATLAB程序运行的结果可得I₃=1.3462A。因I₃的结果为正值，所以I₃的实际方向与参考方向相一致。求解的数据用Multisim软件仿真测试的结果如图1-18所示。

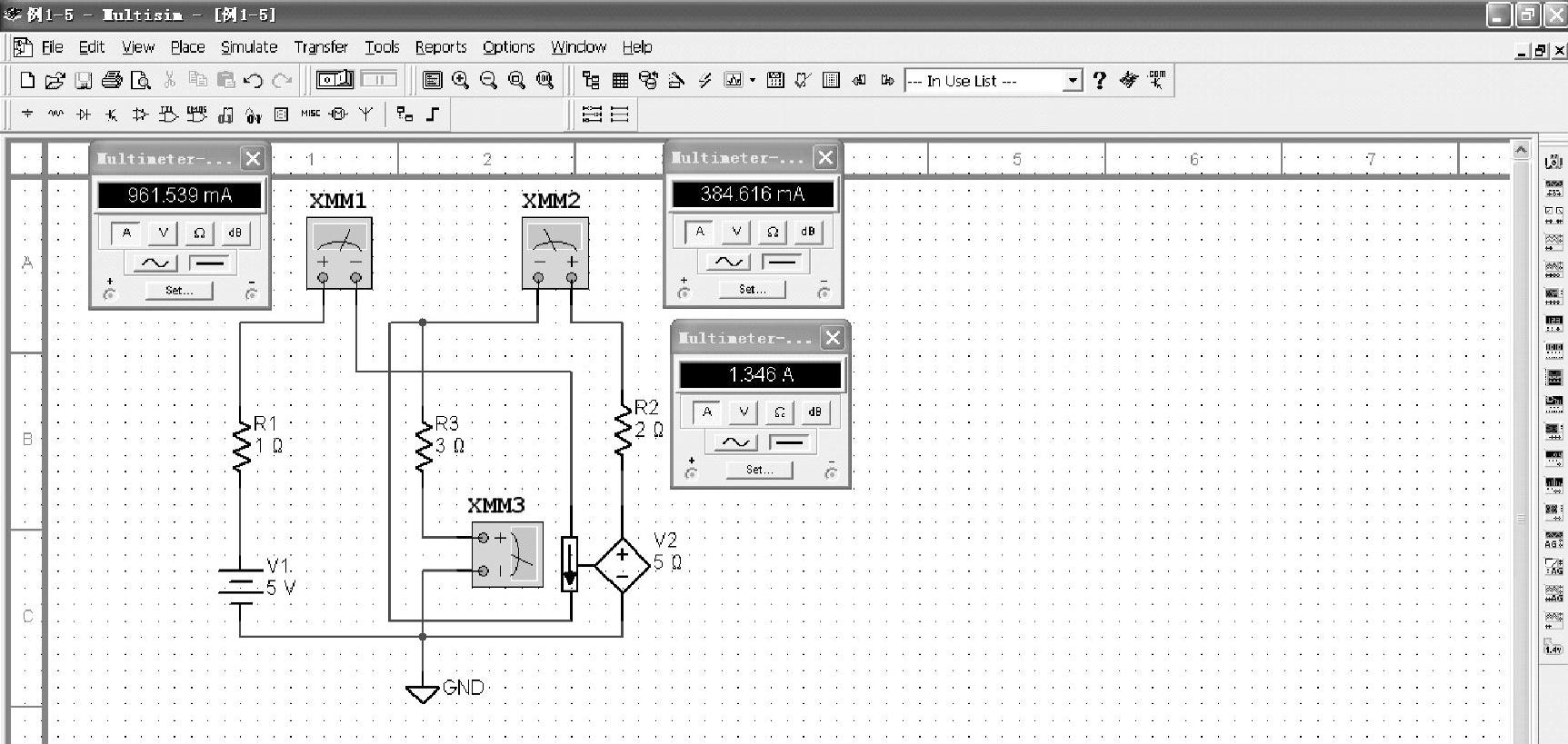
图1-18 例1-5用Multisim软件仿真测试的结果

图1-18中的V₂电源是受控电压源，万用表面板上的数据与理论计算的结果相吻合。

求解此类电路问题还有网孔电流法和回路电流法，这两种方法解题的分析思路和步骤与支路电流法相同，差别仅在于未知量用网孔电流或回路电流来代替支路电流。利用网孔电流或回路电流来代替支路电流可使未知量的数目减少，以减少方程组的方程数。

利用支路电流法理论上可以求解各种复杂电路的问题，但支路电流法求解电路问题的关键是列方程组和解方程组。在许多电路分析的问题中，并不需要计算出各个支路电流和电压的值，而仅要求确定某一支路的电流或者电压的值（例1-5的情况），在这种情况下，用支路电流法求解就显得较麻烦，因此有必要研究分析电路问题的特殊方法。

这些特殊方法与支路电流法所研究的问题相同，都是求解给定电路的电流或者电压的值，所不同的是，在某些场合下，利用这些特殊方法可以简化求解的过程，突出某个参量的物理意义。下面分别来介绍电路分析的几种特殊方法。