判断电功率、电源和负载的方法

电流在电路中流动，用电器要吸收电场的能量，并将其转换成其他形式的能量，如图1-9所示，研究电路能量转换的问题，也是对电路进行分析和计算的一个重要内容。

在图1-9所示的电路中，电源电动势E为电路提供电能，在忽略电源内阻的情况下，负载电阻R_L上消耗的电能可根据电压的定义式来计算。

根据电压的定义式，正电荷Q在电场力的作用下，从a点通过负载R_L移动到b点的过程中，电场力所做的功W为

W=QU=IUt （1-14）

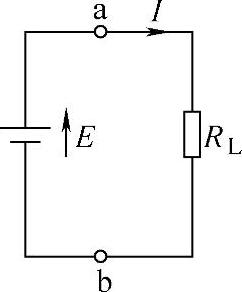
图1-9 电路能量转换的关系

W就是负载在时间t内所消耗的电场能量。当负载是纯电阻器件时，可将欧姆定律代入式（1-14）中，得到纯电阻R_L所消耗的电场能量W_R为

在国际单位制中，电能的单位为焦耳，简称焦（J）。单位时间内负载所吸收的电能称为电功率，简称功率，用字母P来表示，在国际单位制中，功率的单位是瓦特，简称瓦（W）。

功率P的表达式为

对于线性电阻电路，功率P的表达式为

(www.xing528.com)

注意，当电流和电压的参考方向为相关联时，式（1-14）和式（1-16）对任何器件均适用，而式（1-15）和式（1-17）仅适用于线性电阻电路。当电流和电压的参考方向为非关联时，式（1-14）和式（1-16）等式的右边需加一负号。即

P=-IU （1-18）

在图1-9中，电阻R_L上电流和电压的参考方向是关联的，根据式（1-16）计算得到的功率P为正数，说明电阻R_L吸收电场的能量，并将其转换成其他形式的能量，是电路的负载；电源E上的电流和电压的参考方向为非关联，计算电源E的功率必须用式（1-18），计算出来的结果为负值，说明该器件不是消耗电路的能量，而是向电路提供能量，是电路的电源。

根据上面的讨论可知，利用P大于零或小于零的特点，可以判断某一个器件在电路中是承担负载或电源的角色。

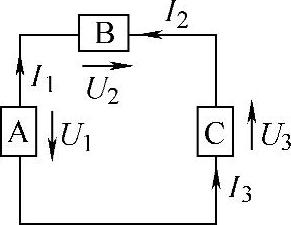
图1-10 例1-2图

【例1-2】 图1-10电路中的A、B、C为三个不同性质的电子器件，各器件上电流、电压参考方向的设定如图所示。已知I₁=2A，I₂=I₃=-2A，U₁=20V，U₂=5V，U₃=-15V，计算各器件的功率，并根据计算结果判断各器件的性质。

解 因为器件A、B上电流和电压的参考方向为非关联，而器件C上电流和电压的参考方向为关联，根据式（1-18）和式（1-16）可得

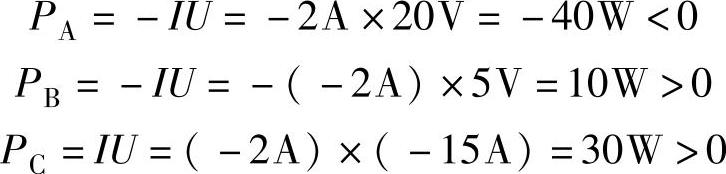
根据P_A小于零的计算结果，可得器件A的性质是电源；根据P_B和P_C大于零的计算结果，可得器件B和器件C的性质是负载。

当电路的电流和电压均是时间的函数时，功率也是时间的函数，在电流和电压的参考方向相关联时，计算功率的表达式为